Cooling Tank Model Optimization
This notebook demonstrates the optimization of the tank model described in tank_optimization_model.py using the ProblemInterface class in the fmdtools.search module.
Note that this problem/notebook was loosely adapted from the identical problem here: https://github.com/DesignEngrLab/resil_opt_examples/tree/main/Cooling%20Tank%20Problem, which shows more comparisions of these architectures running on an earlier version of fmdtools.
Copyright © 2024, United States Government, as represented by the Administrator of the National Aeronautics and Space Administration. All rights reserved.
The “"Fault Model Design tools - fmdtools version 2"” software is licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0.
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
[1]:
from tank_optimization_model import Tank
from fmdtools.define.architecture.function import FunctionArchitectureGraph
from fmdtools.sim import propagate as prop
Simulation
Verifying the nominal state:
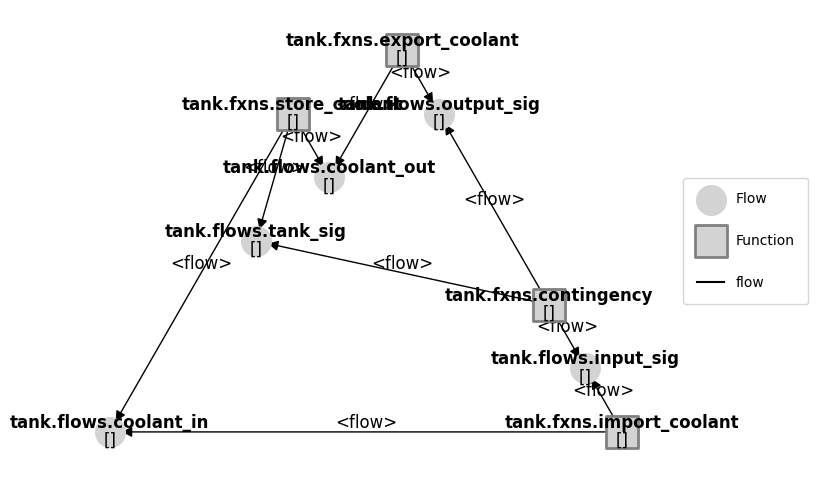
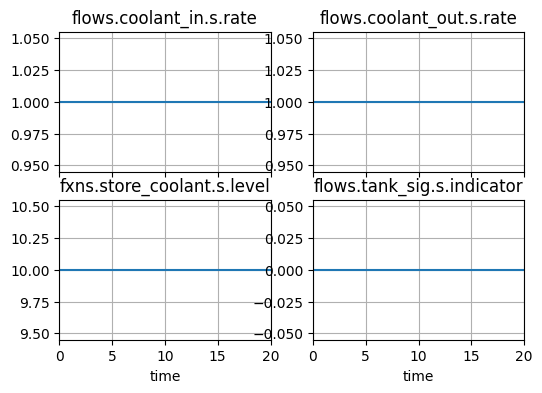
In the nominal state, no change in system state should occurs. Flows will be constant and no signal is on.
[2]:
mdl = Tank()
result, mdlhist = prop.nominal(mdl, track='all', desired_result={'graph': FunctionArchitectureGraph})
[3]:
fig = result.graph.draw(figsize=(8,6))
[4]:
mdlhist
[4]:
flows.coolant_in.s.effort: array(21)
flows.coolant_in.s.rate: array(21)
flows.coolant_out.s.effort: array(21)
flows.coolant_out.s.rate: array(21)
flows.input_sig.s.indicator: array(21)
flows.input_sig.s.action: array(21)
flows.tank_sig.s.indicator: array(21)
flows.tank_sig.s.action: array(21)
flows.output_sig.s.indicator: array(21)
flows.output_sig.s.action: array(21)
fxns.import_coolant.s.amt_open: array(21)
fxns.import_coolant.m.faults.stuck: array(21)
fxns.import_coolant.m.faults.blockage: array(21)
fxns.store_coolant.s.level: array(21)
fxns.store_coolant.s.net_flow: array(21)
fxns.store_coolant.s.coolingbuffer: array(21)
fxns.store_coolant.m.faults.leak: array(21)
fxns.export_coolant.s.amt_open: array(21)
fxns.export_coolant.m.faults.stuck: array(21)
fxns.export_coolant.m.faults.blockage: array(21)
time: array(21)
[5]:
fig, ax = mdlhist.plot_line('flows.coolant_in.s.rate', 'flows.coolant_out.s.rate', 'fxns.store_coolant.s.level', 'flows.tank_sig.s.indicator')
What happens under component faults?
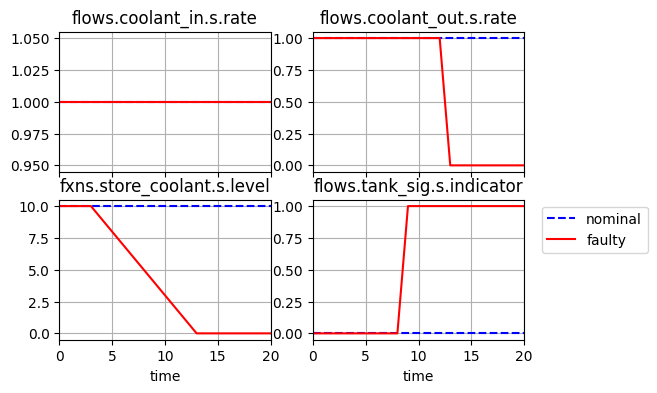
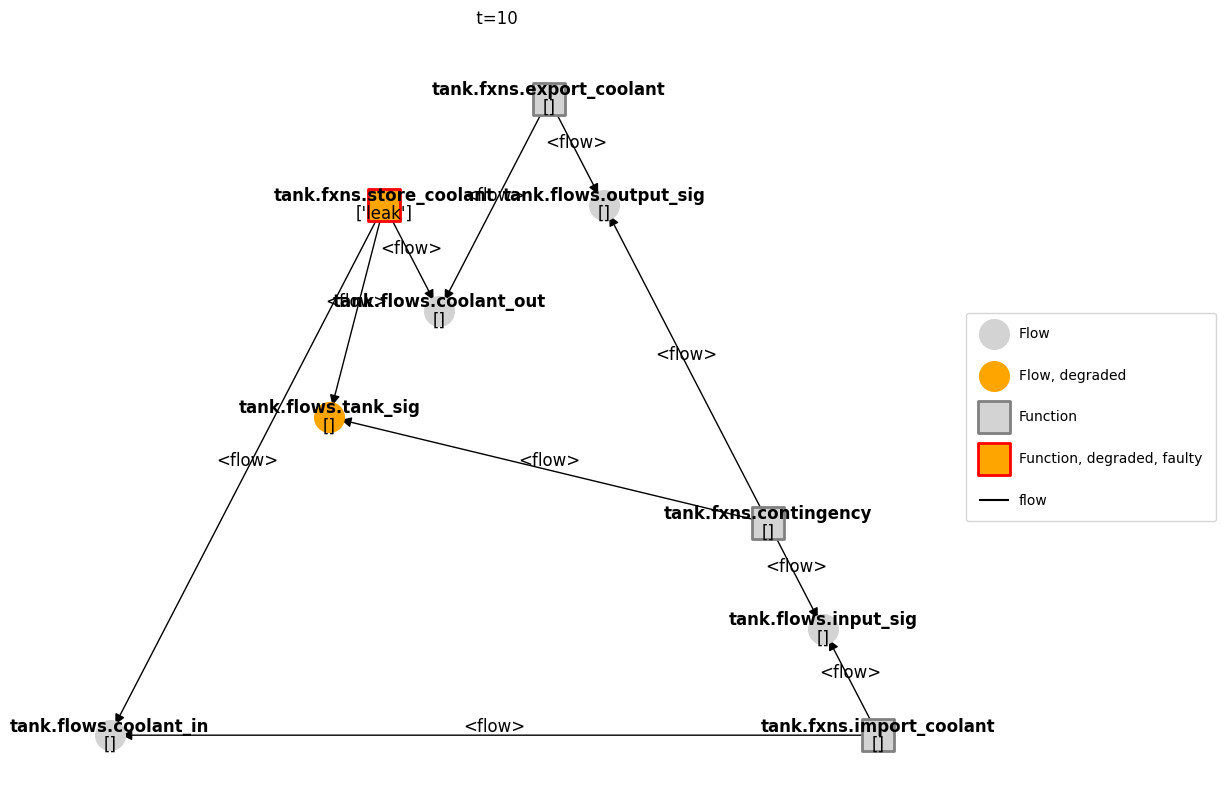
Here we model a leak of the tank. As shown, the coolant leaks until there is no more coolant left in the tank. While this results in a warning signal, the default contingency management policy is to take no actions to alleviate the condition.
[6]:
resgraph, mdlhist = prop.one_fault(mdl,'store_coolant','leak', time=3, track='all',desired_result=['graph','endclass','endfaults'])
fig, ax = mdlhist.plot_line('flows.coolant_in.s.rate', 'flows.coolant_out.s.rate', 'fxns.store_coolant.s.level', 'flows.tank_sig.s.indicator')
[7]:
mg = FunctionArchitectureGraph(mdl)
fig, ax = mg.draw_from(10, mdlhist)
Full set of modes
The tank leak mode will not be the only mode considered, but also leak and blockage faults in the Input/Output blocks.
[8]:
from fmdtools.sim.sample import FaultDomain, FaultSample
fd = FaultDomain(mdl)
fd.add_all()
fd
[8]:
FaultDomain with faults:
-('import_coolant', 'stuck')
-('import_coolant', 'blockage')
-('store_coolant', 'leak')
-('export_coolant', 'stuck')
-('export_coolant', 'blockage')
[9]:
fs = FaultSample(fd)
fs.add_fault_phases("na")
fs
[9]:
FaultSample of scenarios:
- import_coolant_stuck_t0p0
- import_coolant_blockage_t0p0
- store_coolant_leak_t0p0
- export_coolant_stuck_t0p0
- export_coolant_blockage_t0p0
We can then verify the faulty results:
[10]:
endclasses, mdlhists = prop.fault_sample(mdl, fs)
SCENARIOS COMPLETE: 100%|██████████| 5/5 [00:00<00:00, 108.70it/s]
[11]:
from fmdtools.analyze.tabulate import result_summary_fmea
fmea_tab = result_summary_fmea(endclasses, mdlhists)
fmea_tab
[11]:
| degraded | faulty | rate | cost | expected_cost | |
|---|---|---|---|---|---|
| import_coolant_stuck_t0p0 | [] | [] | 0.0 | 0.0 | 0.0 |
| import_coolant_blockage_t0p0 | [] | [] | 0.0 | 2100000.0 | 35000.0 |
| store_coolant_leak_t0p0 | [] | [] | 0.00001 | 1000000.0 | 1000000.0 |
| export_coolant_stuck_t0p0 | [] | [] | 0.0 | 0.0 | 0.0 |
| export_coolant_blockage_t0p0 | [] | [] | 0.0 | 100000.0 | 1666.666667 |
| nominal | [] | [] | 1.0 | 0.0 | 0.0 |
Defining Optimization Problem
We can define a compbined optimization problem around this model using the OptimizationArchitecture, ParameterSimProblem, and SimpleProblem classes.
In this case, we consider the joint minimization of design cost (defined in a function) and resilience cost (expected cost over the above list of scenarios). This is over two sets of variables
capacity and turnup (design variables that effect both design and resilience costs), and
the resilience policy (variables that only effect resilience cost)
To model design cost (which does not involve simulation), we first define a SimpleProblem which calls a predefined function:
[12]:
def x_to_descost(*xdes):
pen = 0 #determining upper-level penalty
if xdes[0]<10:
pen+=1e5*(10-xdes[0])**2
if xdes[0]>100:
pen+=1e5*(100-xdes[0])**2
if xdes[1]<0:
pen+=1e5*(xdes[1])**2
if xdes[1]>1:
pen+=1e5*(1-xdes[1])**2
return (xdes[0]-10)*1000 + (xdes[0]-10)**2*1000 + xdes[1]**2*10000 + pen
[13]:
from fmdtools.sim.search import SimpleProblem
sp = SimpleProblem("capacity", "turnup")
sp.add_objective("cd", x_to_descost)
[14]:
sp.cd(1, 1)
[14]:
8182000.0
[15]:
sp
[15]:
SimpleProblem with:
VARIABLES
-capacity 1.0000
-turnup 1.0000
OBJECTIVES
-cd 8182000.0000
To optimize resilience costs, we can additionally use ParameterSimProblem:
[16]:
from fmdtools.sim.search import ParameterSimProblem
from fmdtools.sim.sample import ParameterDomain
The ParameterDomain is defined by “capacity” and “turnup” variables, as well as the resilience policy:
[17]:
from tank_optimization_model import TankParam
pd = ParameterDomain(TankParam)
pd.add_variables("capacity", "turnup")
The resilience policy is translated using x_to_fp
[18]:
from tank_optimization_model import x_to_fp
fp_varnames = ['faultpolicy.'+str(i) for i, v in enumerate(TankParam.__defaults__['faultpolicy'])]
pd.add_variables(*fp_varnames, var_map=x_to_fp)
[19]:
fp_vars = [1 for i, v in enumerate(TankParam.__defaults__['faultpolicy'])]
[20]:
pd(1, 1, *fp_vars)
[20]:
TankParam(capacity=1.0, turnup=1.0, faultpolicy=((-1, -1, -1, 'l', 1), (-1, -1, 0, 'l', 1), (-1, -1, 1, 'l', 1), (-1, 0, -1, 'l', 1), (-1, 0, 0, 'l', 1), (-1, 0, 1, 'l', 1), (-1, 1, -1, 'l', 1), (-1, 1, 0, 'l', 1), (-1, 1, 1, 'l', 1), (0, -1, -1, 'l', 1), (0, -1, 0, 'l', 1), (0, -1, 1, 'l', 1), (0, 0, -1, 'l', 1), (0, 0, 0, 'l', 1), (0, 0, 1, 'l', 1), (0, 1, -1, 'l', 1), (0, 1, 0, 'l', 1), (0, 1, 1, 'l', 1), (1, -1, -1, 'l', 1), (1, -1, 0, 'l', 1), (1, -1, 1, 'l', 1), (1, 0, -1, 'l', 1), (1, 0, 0, 'l', 1), (1, 0, 1, 'l', 1), (1, 1, -1, 'l', 1), (1, 1, 0, 'l', 1), (1, 1, 1, 'l', 1), (-1, -1, -1, 'u', 1), (-1, -1, 0, 'u', 1), (-1, -1, 1, 'u', 1), (-1, 0, -1, 'u', 1), (-1, 0, 0, 'u', 1), (-1, 0, 1, 'u', 1), (-1, 1, -1, 'u', 1), (-1, 1, 0, 'u', 1), (-1, 1, 1, 'u', 1), (0, -1, -1, 'u', 1), (0, -1, 0, 'u', 1), (0, -1, 1, 'u', 1), (0, 0, -1, 'u', 1), (0, 0, 0, 'u', 1), (0, 0, 1, 'u', 1), (0, 1, -1, 'u', 1), (0, 1, 0, 'u', 1), (0, 1, 1, 'u', 1), (1, -1, -1, 'u', 1), (1, -1, 0, 'u', 1), (1, -1, 1, 'u', 1), (1, 0, -1, 'u', 1), (1, 0, 0, 'u', 1), (1, 0, 1, 'u', 1), (1, 1, -1, 'u', 1), (1, 1, 0, 'u', 1), (1, 1, 1, 'u', 1)), policymap={(-1, -1, -1): (1, 1), (-1, -1, 0): (1, 1), (-1, -1, 1): (1, 1), (-1, 0, -1): (1, 1), (-1, 0, 0): (1, 1), (-1, 0, 1): (1, 1), (-1, 1, -1): (1, 1), (-1, 1, 0): (1, 1), (-1, 1, 1): (1, 1), (0, -1, -1): (1, 1), (0, -1, 0): (1, 1), (0, -1, 1): (1, 1), (0, 0, -1): (1, 1), (0, 0, 0): (1, 1), (0, 0, 1): (1, 1), (0, 1, -1): (1, 1), (0, 1, 0): (1, 1), (0, 1, 1): (1, 1), (1, -1, -1): (1, 1), (1, -1, 0): (1, 1), (1, -1, 1): (1, 1), (1, 0, -1): (1, 1), (1, 0, 0): (1, 1), (1, 0, 1): (1, 1), (1, 1, -1): (1, 1), (1, 1, 0): (1, 1), (1, 1, 1): (1, 1)})
[21]:
pd
[21]:
ParameterDomain with:
- variables: {'capacity': (), 'turnup': (), 'faultpolicy.0': (), 'faultpolicy.1': (), 'faultpolicy.2': (), 'faultpolicy.3': (), 'faultpolicy.4': (), 'faultpolicy.5': (), 'faultpolicy.6': (), 'faultpolicy.7': (), 'faultpolicy.8': (), 'faultpolicy.9': (), 'faultpolicy.10': (), 'faultpolicy.11': (), 'faultpolicy.12': (), 'faultpolicy.13': (), 'faultpolicy.14': (), 'faultpolicy.15': (), 'faultpolicy.16': (), 'faultpolicy.17': (), 'faultpolicy.18': (), 'faultpolicy.19': (), 'faultpolicy.20': (), 'faultpolicy.21': (), 'faultpolicy.22': (), 'faultpolicy.23': (), 'faultpolicy.24': (), 'faultpolicy.25': (), 'faultpolicy.26': (), 'faultpolicy.27': (), 'faultpolicy.28': (), 'faultpolicy.29': (), 'faultpolicy.30': (), 'faultpolicy.31': (), 'faultpolicy.32': (), 'faultpolicy.33': (), 'faultpolicy.34': (), 'faultpolicy.35': (), 'faultpolicy.36': (), 'faultpolicy.37': (), 'faultpolicy.38': (), 'faultpolicy.39': (), 'faultpolicy.40': (), 'faultpolicy.41': (), 'faultpolicy.42': (), 'faultpolicy.43': (), 'faultpolicy.44': (), 'faultpolicy.45': (), 'faultpolicy.46': (), 'faultpolicy.47': (), 'faultpolicy.48': (), 'faultpolicy.49': (), 'faultpolicy.50': (), 'faultpolicy.51': (), 'faultpolicy.52': (), 'faultpolicy.53': ()}
- constants: {}
- parameter_initializer: TankParam
Which we then use to define the problem:
[22]:
from multiprocessing import Pool
psp = ParameterSimProblem(mdl, pd, "fault_sample", fs, pool=Pool(5), close_pool=False)
psp.add_result_objective("cr", "endclass.expected_cost")
[23]:
psp.cr(1, 2, *fp_vars)
[23]:
4201123133.3333335
[24]:
psp.cr(0.5, 1, *fp_vars)
[24]:
4201124800.0
Since the design variables affect both design and resilience costs, we can connect these two problems in an overall ProblemArchitecture where design cost evaluation feeds into resilience cost evaluation.
First, we define a simpleproblem to combine the objectives:
[25]:
def tot(c_d, c_o):
return c_d + c_o
tot_sp = SimpleProblem("cd", "cr")
tot_sp.add_objective("tot_cost", tot)
tot_sp.tot_cost(1, 1)
[25]:
2
[26]:
from fmdtools.sim.search import ProblemArchitecture
pa = ProblemArchitecture()
[27]:
pa.add_connector_variable("xd", "capacity", "turnup")
pa.add_connector_objective("dcost", "cd")
pa.add_connector_objective("rcost", "cr")
[28]:
pa.add_problem("des", sp, outputs={"xd": ("capacity", "turnup"), "dcost": ("cd", )})
pa.add_problem("res", psp, inputs={"xd": ("capacity", "turnup")}, outputs={"rcost": ("cr", )})
pa.add_problem("tot", tot_sp, inputs={"dcost": ("cd", ), "rcost": ("cr", )})
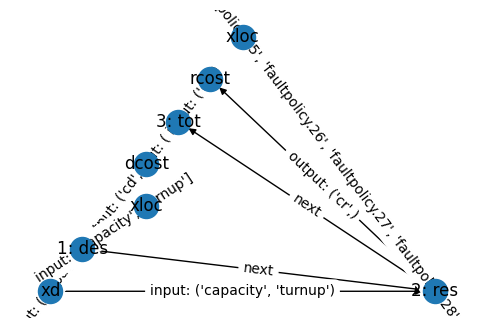
We can then visualize/verify the setup of this using:
[29]:
fig, ax = pa.show_sequence()
[30]:
pa.connectors['xd']
[30]:
VariableConnector(name='xd', keys=('capacity', 'turnup'), values=array([nan, nan]))
[31]:
pa
[31]:
ProblemArchitecture with:
CONNECTORS
-xd [nan nan]
-dcost [nan]
-rcost [nan]
PROBLEMS
-des({'des_xloc': ['capacity', 'turnup']}) -> ['xd', 'dcost']
-res({'xd': ('capacity', 'turnup'), 'res_xloc': ['faultpolicy.0', 'faultpolicy.1', 'faultpolicy.2', 'faultpolicy.3', 'faultpolicy.4', 'faultpolicy.5', 'faultpolicy.6', 'faultpolicy.7', 'faultpolicy.8', 'faultpolicy.9', 'faultpolicy.10', 'faultpolicy.11', 'faultpolicy.12', 'faultpolicy.13', 'faultpolicy.14', 'faultpolicy.15', 'faultpolicy.16', 'faultpolicy.17', 'faultpolicy.18', 'faultpolicy.19', 'faultpolicy.20', 'faultpolicy.21', 'faultpolicy.22', 'faultpolicy.23', 'faultpolicy.24', 'faultpolicy.25', 'faultpolicy.26', 'faultpolicy.27', 'faultpolicy.28', 'faultpolicy.29', 'faultpolicy.30', 'faultpolicy.31', 'faultpolicy.32', 'faultpolicy.33', 'faultpolicy.34', 'faultpolicy.35', 'faultpolicy.36', 'faultpolicy.37', 'faultpolicy.38', 'faultpolicy.39', 'faultpolicy.40', 'faultpolicy.41', 'faultpolicy.42', 'faultpolicy.43', 'faultpolicy.44', 'faultpolicy.45', 'faultpolicy.46', 'faultpolicy.47', 'faultpolicy.48', 'faultpolicy.49', 'faultpolicy.50', 'faultpolicy.51', 'faultpolicy.52', 'faultpolicy.53']}) -> ['rcost']
-tot({'dcost': ('cd',), 'rcost': ('cr',)}) -> []
VARIABLES
-des_xloc [nan nan]
-res_xloc [nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan
nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan
nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan]
OBJECTIVES
-des_cd 8182000.0000
-res_cr nan
-tot_tot_cost nan
We can also evaluate the objectives in terms of full or partial sets of the variables:
[32]:
fp_vars = [0 for i, v in enumerate(TankParam.__defaults__['faultpolicy'])]
pa.res_cr_full(0.5, 1.0, *fp_vars)
[32]:
1081666.6666666667
[33]:
pa
[33]:
ProblemArchitecture with:
CONNECTORS
-xd [0.5 1. ]
-dcost [9115750.]
-rcost [1081666.66666667]
PROBLEMS
-des({'des_xloc': ['capacity', 'turnup']}) -> ['xd', 'dcost']
-res({'xd': ('capacity', 'turnup'), 'res_xloc': ['faultpolicy.0', 'faultpolicy.1', 'faultpolicy.2', 'faultpolicy.3', 'faultpolicy.4', 'faultpolicy.5', 'faultpolicy.6', 'faultpolicy.7', 'faultpolicy.8', 'faultpolicy.9', 'faultpolicy.10', 'faultpolicy.11', 'faultpolicy.12', 'faultpolicy.13', 'faultpolicy.14', 'faultpolicy.15', 'faultpolicy.16', 'faultpolicy.17', 'faultpolicy.18', 'faultpolicy.19', 'faultpolicy.20', 'faultpolicy.21', 'faultpolicy.22', 'faultpolicy.23', 'faultpolicy.24', 'faultpolicy.25', 'faultpolicy.26', 'faultpolicy.27', 'faultpolicy.28', 'faultpolicy.29', 'faultpolicy.30', 'faultpolicy.31', 'faultpolicy.32', 'faultpolicy.33', 'faultpolicy.34', 'faultpolicy.35', 'faultpolicy.36', 'faultpolicy.37', 'faultpolicy.38', 'faultpolicy.39', 'faultpolicy.40', 'faultpolicy.41', 'faultpolicy.42', 'faultpolicy.43', 'faultpolicy.44', 'faultpolicy.45', 'faultpolicy.46', 'faultpolicy.47', 'faultpolicy.48', 'faultpolicy.49', 'faultpolicy.50', 'faultpolicy.51', 'faultpolicy.52', 'faultpolicy.53']}) -> ['rcost']
-tot({'dcost': ('cd',), 'rcost': ('cr',)}) -> []
VARIABLES
-des_xloc [0.5 1. ]
-res_xloc [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.]
OBJECTIVES
-des_cd 9115750.0000
-res_cr 1081666.6667
-tot_tot_cost nan
[34]:
pa.tot_tot_cost_full(0.5, 1.0, *fp_vars)
[34]:
10197416.666666666
Note that because the simulations are linked, changes to xdes in the cd function in turn change the lower-level cost function by default.
[35]:
pa.des_cd(1,1)
[35]:
8182000.0
[36]:
pa.res_cr(*fp_vars)
[36]:
1081666.6666666667
[37]:
pa.tot_tot_cost()
[37]:
9263666.666666666
Optimization
This problem is optimized here using four different architectures, following the example in:
Hulse, D., & Hoyle, C. (2022). Understanding Resilience Optimization Architectures: Alignment and Coupling in Multilevel Decomposition Strategies. Journal of Mechanical Design, 144(11), 111704.
The optimization of the resilience policy is accomplished using an evolutionary algorithm, defined below:
[38]:
import numpy as np
import random
def EA(prob_callable, popsize=10, iters=20, mutations=3, crossovers=2, numselect=3, verbose=True, args={}):
# generate initial population:
randpopsize = popsize-numselect-mutations - crossovers
opers = [randpop, mutepop, crossover]
numopers = [randpopsize, mutations, crossovers]
used_opers = [oper for i, oper in enumerate(opers) if numopers[i] > 0]
used_numopers = [numoper for numoper in numopers if numoper > 0]
if args:
pop = np.concatenate((args['seed'], seedpop(), randpop([], popsize-3)))
else:
pop = np.concatenate((seedpop(), randpop([], popsize-3)))
makefeasible(pop)
# evaluate initial population
values = np.array([prob_callable(*[*x[0], *x[1]]) for x in pop])
# gen/evaluate mutated population
for i in range(iters):
goodpop, goodvals = select(pop, values, numselect)
newpop = np.concatenate(tuple([oper(goodpop, used_numopers[i]) for i, oper in enumerate(used_opers)]))
makefeasible(newpop)
newvals = np.array([prob_callable(*[*x[0], *x[1]]) for x in newpop])
pop, values = np.concatenate(
(goodpop, newpop)), np.concatenate((goodvals, newvals))
if verbose == "iters":
print(["iter "+str(i)+": ", min(values)])
minind = np.argmin(values)
if args:
args['seed'] = goodpop
args['ll_opt'] = values[minind]
args['ll_optx'] = pop[minind]
if verbose == "final":
print(values[minind])
return pop[minind], values[minind]
possible_sols = [[-1, -1], [-1, 0], [-1, 1],
[0, -1], [0, 0], [0, 1], [1, -1], [1, 0], [1, 1]]
def randpop(goodpop, popsize):
return np.array([[[random.randint(-1, 1) for a in range(0, 27)],
[random.randint(-1, 1) for a in range(0, 27)]]
for i in range(0, popsize)])
def seedpop():
donothing = np.zeros((2, 27))
adjustup = np.ones((2, 27))
adjustdown = -np.ones((2, 27))
return np.array([donothing, adjustup, adjustdown])
def mutepop(goodpop, mutations):
to_mutate = np.random.choice(
[i for i in range(len(goodpop))], size=mutations, replace=False)
return np.array([permute(solution) for solution in goodpop[to_mutate]])
def permute(solution):
mutation = possible_sols[random.randint(0, 8)]
to_mutate = random.randint(0, 26)
solution[0][to_mutate] = mutation[0]
solution[1][to_mutate] = mutation[1]
return solution
def crossover(goodpop, crossovers):
to_cross = np.random.choice(
[i for i in range(len(goodpop))], size=crossovers, replace=False)
divider = np.random.randint(1, 25)
swap = np.random.choice([i for i in range(crossovers)],
size=crossovers, replace=False)
return np.array([[np.concatenate((goodpop[to_cross[i]][0][:divider], goodpop[to_cross[swap[i]]][0][divider:])), np.concatenate((goodpop[to_cross[i]][1][:divider], goodpop[to_cross[swap[i]]][1][divider:]))] for i in range(crossovers)])
def select(solutions, values, numselect):
selection = np.argsort(values)[0:numselect]
return solutions[selection], values[selection]
def makefeasible(population):
for sol in population:
sol[0][13] = 0
sol[1][13] = 0
[39]:
pop, vals = EA(pa.res_cr, verbose = 'iters')
['iter 0: ', 1081666.6666666667]
['iter 1: ', 1081666.6666666667]
['iter 2: ', 1081666.6666666667]
['iter 3: ', 1081666.6666666667]
['iter 4: ', 1081666.6666666667]
['iter 5: ', 1081666.6666666667]
['iter 6: ', 1081666.6666666667]
['iter 7: ', 1081666.6666666667]
['iter 8: ', 1081666.6666666667]
['iter 9: ', 1081666.6666666667]
['iter 10: ', 1081666.6666666667]
['iter 11: ', 1081666.6666666667]
['iter 12: ', 1081666.6666666667]
['iter 13: ', 1081666.6666666667]
['iter 14: ', 1081666.6666666667]
['iter 15: ', 1081666.6666666667]
['iter 16: ', 1081666.6666666667]
['iter 17: ', 1081666.6666666667]
['iter 18: ', 1081666.6666666667]
['iter 19: ', 1081666.6666666667]
[41]:
fig, axs = pa.plot_opt_hist()
C:\Users\dhulse\Documents\GitHub\fmdtools\fmdtools\sim\search.py:349: RuntimeWarning: All-NaN slice encountered
hist[val] = [np.nanmin(arr[:i]) for i in range(1, len(arr)+1)]
Alternating Optimization
Which can then be optimized in an alternating or bilevel optimization structure:
[41]:
from scipy.optimize import minimize
def sub_totcost(tot_cost_callable):
def new_func(xres, args):
return tot_cost_callable(*xres, *args)
return new_func
def alternating_opt(tot_cost_callable, dcost_callable, rcost_callable, option='with_cr', pool=False, xdes=[21, .5], max_alts=10):
xdes = np.array(xdes)
args = {'seed': seedpop(), 'll_opt': 1e6, 'll_optx': []}
newmin = 100000000
lastmin = 1000000001
bestsol = np.zeros(54)
last_run = False
fhist = []
thist = [0]
xdhist = [xdes]
for n in range(max_alts):
if option == 'with_cr':
tot_cost_call = sub_totcost(tot_cost_callable)
result = minimize(tot_cost_call,
[np.round(xdes[0], 1), np.round(xdes[1], 1)],
method='Nelder-Mead',
bounds=((10, 100), (0, 1)),
callback=callbackF1,
args=bestsol,
options={'disp': True})
else:
result = minimize(dcost_callable,
[np.round(xdes[0], 1),
np.round(xdes[1], 1)],
method='Nelder-Mead',
bounds=((10, 100), (0, 1)),
callback=callbackF1,
options={'disp': True})
xdes = result['x']
dcost = dcost_callable(*xdes)
bestpop, rcost = EA(rcost_callable, args=args, popsize=50, mutations=10,
numselect=20, crossovers=5, iters=100, verbose="iters")
bestsol = [*bestpop[0], *bestpop[1]]
lastmin = newmin
newmin = dcost + rcost
fhist.append(newmin)
xdhist.append(xdes)
print(n, newmin, lastmin-newmin)
if lastmin - newmin < 0.1:
if last_run:
break
else:
last_run = True
else:
last_run = False
fhist.append(newmin)
return result, args, fhist, thist, xdhist
def callbackF(Xdes, result):
print('{0:4d} {1: 3.6f} {2: 3.6f} {3: 3.6f}'.format(
result['nit'], Xdes[0], Xdes[1], result['fun']))
def callbackF1(Xdes):
print(Xdes)
[42]:
result, args, fhist, thist, xdhist = alternating_opt(pa.tot_tot_cost_full, pa.des_cd, pa.res_cr, max_alts=1)
[18.9 0.5375]
[17.85 0.50625]
[13.125 0.565625]
[12.075 0.534375]
[12.075 0.534375]
[12.075 0.534375]
[12.075 0.503125]
[12.075 0.503125]
[12.075 0.503125]
[12.075 0.503125]
[12.075 0.503125]
[12.075 0.503125]
[12.01015625 0.50839844]
[12.01015625 0.50058594]
[12.01015625 0.50058594]
[12.01015625 0.50058594]
[12.01015625 0.50058594]
[12.01015625 0.50058594]
[12.00610352 0.48699951]
[12.00610352 0.48699951]
[12.00863647 0.47205353]
[12.00154419 0.46390228]
[12.00306396 0.42993469]
[12.00306396 0.42993469]
[12.00971298 0.40632648]
[12.00822487 0.33541975]
[12.02077885 0.25274997]
[12.02407961 0.06960161]
[12.02407961 0.06960161]
[12.02407961 0.06960161]
[12.0225915 0.06960161]
[12.02924051 0.0348008 ]
[12.0277524 0.0348008]
[12.0277524 0.0348008]
[12.02146354 0.06090141]
[12.02273595 0.0391509 ]
[12.01079444 0.08047686]
[12.00736851 0.05763883]
[12.00736851 0.05763883]
[12.00736851 0.05763883]
[12.00394258 0.0348008 ]
[12.00394258 0.0348008 ]
[12.00478061 0. ]
[12.00478061 0. ]
[1.20020078e+01 6.72906165e-03]
[1.20020078e+01 6.72906165e-03]
[1.20000730e+01 6.72906165e-03]
[1.20000730e+01 6.72906165e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000084e+01 3.36453082e-03]
[1.20000023e+01 1.87283454e-03]
[1.20000023e+01 1.87283454e-03]
[1.20000023e+01 1.87283454e-03]
[1.20000023e+01 1.87283454e-03]
[1.20000024e+01 8.16900855e-04]
[1.20000024e+01 8.16900855e-04]
[1.20000024e+01 8.16900855e-04]
[1.20000024e+01 8.16900855e-04]
[12.00000087 0. ]
[12.00000087 0. ]
[12.00000087 0. ]
[12.00000087 0. ]
[12.00000041 0. ]
[12.00000041 0. ]
[12.00000041 0. ]
[12.0000003 0. ]
[12.0000003 0. ]
[12.0000001 0. ]
[12.0000001 0. ]
[12.0000001 0. ]
[12.0000001 0. ]
[12.0000001 0. ]
[12.00000005 0. ]
[12.00000001 0. ]
[12.00000001 0. ]
[12.00000001 0. ]
[12.00000001 0. ]
[12.00000001 0. ]
[12.00000001 0. ]
Optimization terminated successfully.
Current function value: 1057666.666717
Iterations: 86
Function evaluations: 167
['iter 0: ', 1051666.6666666667]
['iter 1: ', 1051666.6666666667]
['iter 2: ', 1051666.6666666667]
['iter 3: ', 1051666.6666666667]
['iter 4: ', 1051666.6666666667]
['iter 5: ', 1051666.6666666667]
['iter 6: ', 1050000.0]
['iter 7: ', 1049900.0]
['iter 8: ', 1049900.0]
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[42], line 1
----> 1 result, args, fhist, thist, xdhist = alternating_opt(pa.tot_tot_cost_full, pa.des_cd, pa.res_cr, max_alts=1)
Cell In[41], line 38, in alternating_opt(tot_cost_callable, dcost_callable, rcost_callable, option, pool, xdes, max_alts)
36 xdes = result['x']
37 dcost = dcost_callable(*xdes)
---> 38 bestpop, rcost = EA(rcost_callable, args=args, popsize=50, mutations=10,
39 numselect=20, crossovers=5, iters=100, verbose="iters")
40 bestsol = [*bestpop[0], *bestpop[1]]
41 lastmin = newmin
Cell In[38], line 22, in EA(prob_callable, popsize, iters, mutations, crossovers, numselect, verbose, args)
20 newpop = np.concatenate(tuple([oper(goodpop, used_numopers[i]) for i, oper in enumerate(used_opers)]))
21 makefeasible(newpop)
---> 22 newvals = np.array([prob_callable(*[*x[0], *x[1]]) for x in newpop])
23 pop, values = np.concatenate(
24 (goodpop, newpop)), np.concatenate((goodvals, newvals))
25 if verbose == "iters":
Cell In[38], line 22, in <listcomp>(.0)
20 newpop = np.concatenate(tuple([oper(goodpop, used_numopers[i]) for i, oper in enumerate(used_opers)]))
21 makefeasible(newpop)
---> 22 newvals = np.array([prob_callable(*[*x[0], *x[1]]) for x in newpop])
23 pop, values = np.concatenate(
24 (goodpop, newpop)), np.concatenate((goodvals, newvals))
25 if verbose == "iters":
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\search.py:1288, in ProblemArchitecture.add_objective_callable.<locals>.newobj(*x)
1287 def newobj(*x):
-> 1288 return self.call_objective(probname, objname, *x)
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\search.py:1353, in ProblemArchitecture.call_objective(self, probname, objname, *x_loc)
1351 def call_objective(self, probname, objname, *x_loc):
1352 """Call objective of a problem over partial its local variables *x_loc."""
-> 1353 self.update_problem(probname, *x_loc)
1354 return self.problems[probname].objectives[objname].value
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\search.py:1466, in ProblemArchitecture.update_problem(self, probname, force_update, *x)
1464 self.update_problem(upstream_prob, force_update=force_update)
1465 x_inputs = self.get_inputs_as_x(probname, *x)
-> 1466 self.problems[probname].call_outputs(*x_inputs, force_update=force_update)
1467 self.problems[probname].consistent = True
1468 self.update_problem_objectives(probname)
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\search.py:233, in BaseProblem.call_outputs(self, force_update, *x)
217 """
218 Get all outputs at the given value of x.
219
(...)
230 values of the constraints
231 """
232 if self.new_x(*x) or force_update:
--> 233 self.update_objectives(*x)
234 return self.get_objectives(), self.get_constraints()
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\search.py:599, in BaseSimProblem.update_objectives(self, *x)
597 """Update objectives/constraints by simulating the model at x."""
598 self.update_variables(*x)
--> 599 self.res, self.hist = self.sim_mdl(*x)
600 for obj in {**self.objectives, **self.constraints}.values():
601 if isinstance(obj, HistoryObjective) or isinstance(obj, HistoryConstraint):
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\search.py:709, in ParameterSimProblem.sim_mdl(self, *x)
707 mdl_kwargs = {'p': p, 'sp': {'end_time': end_time}}
708 desired_result = self.obj_con_des_res()
--> 709 all_res = self.prop_method(self.mdl.new(),
710 *self.args,
711 mdl_kwargs=mdl_kwargs,
712 desired_result=desired_result,
713 showprogress=False,
714 **self.kwargs)
715 return all_res[0].flatten(), all_res[1].flatten()
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\propagate.py:621, in fault_sample(mdl, fs, include_nominal, get_phasemap, **kwargs)
618 nomresult, nomhist, nomscen, c_mdl, t_end_nom = n_outs
619 scenlist = fs.scenarios()
--> 621 results, mdlhists = scenlist_helper(mdl,
622 scenlist,
623 c_mdl,
624 **kwargs,
625 nomhist=nomhist,
626 nomresult=nomresult)
628 if include_nominal:
629 process_nominal(mdlhists, nomhist, results, nomresult, t_end_nom, **kwargs)
File c:\users\dhulse\documents\github\fmdtools\fmdtools\sim\propagate.py:779, in scenlist_helper(mdl, scenlist, c_mdl, **kwargs)
776 else:
777 inputs = [(c_mdl[0], scen, kwargs, str(i))
778 for i, scen in enumerate(scenlist)]
--> 779 res_list = list(tqdm.tqdm(pool.map(exec_scen_par, inputs),
780 total=len(inputs),
781 disable=not (showprogress),
782 desc="SCENARIOS COMPLETE"))
783 results, mdlhists = unpack_res_list(scenlist, res_list)
784 else:
File ~\AppData\Local\anaconda3\lib\multiprocessing\pool.py:367, in Pool.map(self, func, iterable, chunksize)
362 def map(self, func, iterable, chunksize=None):
363 '''
364 Apply `func` to each element in `iterable`, collecting the results
365 in a list that is returned.
366 '''
--> 367 return self._map_async(func, iterable, mapstar, chunksize).get()
File ~\AppData\Local\anaconda3\lib\multiprocessing\pool.py:768, in ApplyResult.get(self, timeout)
767 def get(self, timeout=None):
--> 768 self.wait(timeout)
769 if not self.ready():
770 raise TimeoutError
File ~\AppData\Local\anaconda3\lib\multiprocessing\pool.py:765, in ApplyResult.wait(self, timeout)
764 def wait(self, timeout=None):
--> 765 self._event.wait(timeout)
File ~\AppData\Local\anaconda3\lib\threading.py:607, in Event.wait(self, timeout)
605 signaled = self._flag
606 if not signaled:
--> 607 signaled = self._cond.wait(timeout)
608 return signaled
File ~\AppData\Local\anaconda3\lib\threading.py:320, in Condition.wait(self, timeout)
318 try: # restore state no matter what (e.g., KeyboardInterrupt)
319 if timeout is None:
--> 320 waiter.acquire()
321 gotit = True
322 else:
KeyboardInterrupt:
Bilevel Optimization:
Additionally, a bilevel optimization would look like this:
Bilevel optimizations have a lower level which is called repeatedly, see below:
[50]:
def lower_level(xdes, args= {}):
if not args:
args = {'seed': seedpop(), 'll_opt': 1e6, 'll_optx': [], 'fhist': []}
do_cost = pa.des_cd(*xdes)
bestsol, rcost = EA(pa.res_cr, popsize=20, mutations=6, crossovers=4, numselect=6, args=args)
f = do_cost + rcost
args['fhist'].append(f)
print(' fval: '+str(f)+' xdes: '+str(xdes))
return f
[51]:
lower_level([1,1])
This is then called in bilevel_opt:
[52]:
def bilevel_opt(xdes=[21, .5], maxiter=1000):
args = {'seed': seedpop(), 'll_opt': 1e6, 'll_optx': [], 'fhist': [],
'thist': [], 'xdhist': [xdes]}
result = minimize(lower_level,
xdes,
method='Nelder-Mead',
bounds=((10, 100), (0, 1)),
callback=callbackF1,
args=args,
options={'disp': True, 'adaptive': True, 'fatol': 10, 'xtol': 0.00001, 'maxiter': maxiter})
fullfhist = args['fhist']
fullxdhist = args['xdhist']
bestfhist = [fullfhist[0]]+[min(fullfhist[:i])
for i, f in enumerate(fullfhist) if i != 0]
return result, args, bestfhist
[53]:
bilevel_opt(maxiter=2)
[ ]:
pool.close()
pool.terminate()
Note that these are the previously-recorded results for different strategies:
𝑥_t |
𝑥_l |
𝑓 |
time |
|
|---|---|---|---|---|
Bilevel |
18.000015 |
0.580982 |
285708.991759 |
619.369699 |
Alt. (no 𝐶 𝑅CR) |
10.000000 |
0.000000 |
893333.333333 |
168.275383 |
Alt. (with 𝐶 𝑅CR) |
20.000000 |
0.000000 |
452666.666823 |
306.776320 |
Seq. (with 𝐶 𝑅CR) |
22.000000 |
0.000000 |
466333.333389 |
61.702104 |
Seq. (no 𝐶 𝑅CR) |
10.000000 |
0.000000 |
893333.333333 |
55.957946 |
Generally, we would expect results to be somewhat consistent with this (not exactly, since the lower-level EA is a stochastic search), however, there have been many changes to the underlying toolkit/model, as well as the tank model which may lead to different results.
[ ]: