Note
Go to the end to download the full example code.
Configuring Models¶
At times, model templates need to be parametrized in a more of a programming sense than a mathematical one. An example of this is a linear time invariant (LTI) ODE system, where the size of the state vector and whether there is feedback control are dependent on what the user passes in for the state and input matrices.
Module Configuration¶
One option for generating models is through a settings object in the top-level
condor name space, where you register the module’s default configuration with
get_settings. Then the module is imported via get_module.
Here is the configured model source with the name _lti.py:
1import numpy as np
2
3import condor
4
5# pass get_settings in a list of configurable variables with defaults
6# it returns a dictionary with the the configured values
7conf = condor.settings.get_settings(A=np.array([1.0]), B=None)
8A, B = conf.values()
9
10
11class LTI(condor.ODESystem):
12 x = state(shape=A.shape[0])
13
14 xdot = A @ x
15
16 if B is not None:
17 K = parameter(shape=B.T.shape)
18
19 u = -K @ x
20 dynamic_output.u = u
21
22 xdot += B @ u
23
24 dot[x] = xdot
To use this module, we use get_module(), passing its declared
settings as concrete keyword arguments.
The returned object is a module, so we can access the model with its declared class name:
LTI_dblint = dblint_mod.LTI
And finally we can use this configured ODE system to simulate a trajectory.
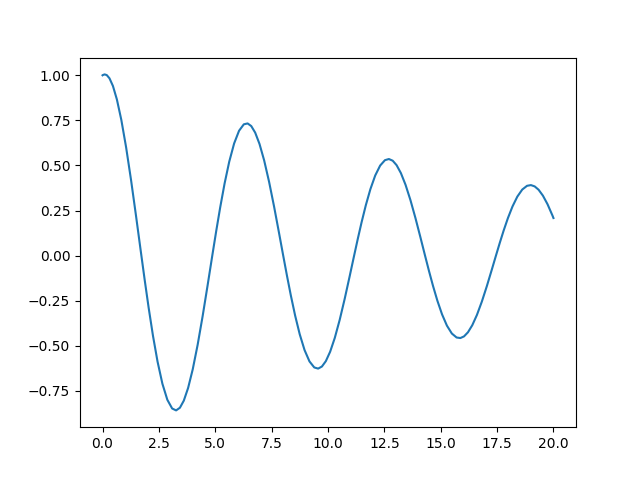
[<matplotlib.lines.Line2D object at 0x7fe1302f1a60>]
We can also re-use the module with a different configuration:
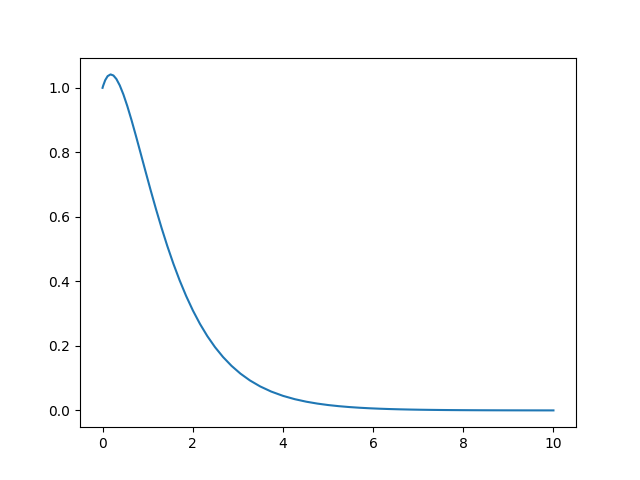
[<matplotlib.lines.Line2D object at 0x7fe1323b6960>]
Programmatic Construction¶
An alternative approach is to programmatically generate the model using the metaprogramming machinery Condor uses internally. See Metaprogramming class declaration for a more thorough overview.
from condor.contrib import ModelTemplateType, ODESystem
def make_LTI(A, B=None, name="LTISystem"):
attrs = ModelTemplateType.__prepare__(name, (ODESystem,))
attrs["A"] = A
state = attrs["state"]
x = state(shape=A.shape[0])
attrs["x"] = x
xdot = A @ x
if B is not None:
attrs["B"] = B
K = attrs["parameter"](shape=B.T.shape)
attrs["K"] = K
u = -K @ x
attrs["dynamic_output"].u = u
xdot += B @ u
attrs["dot"][x] = xdot
plant = ModelTemplateType(name, (ODESystem,), attrs)
return plant
# OR for primary models:
ode_attrs = condor.ODESystem.__prepare__(ode_name, (condor.ODESystem,))
ode_model = condor.ODESystem.__class__(ode_name, (condor.ODESystem,), ode_attrs)
# but submodels must be ~ the way shown above:
event_meta_args = (
event_name,
(ode_model.Event, condor.models.Submodel),
)
event_attrs = condor.contrib.Event.__prepare__(*event_meta_args)
condor.contrib.EventType.__new__(
condor.contrib.EventType,
*event_meta_args,
attrs=event_attrs,
)
Use of the model factory function looks similar to using get_module:
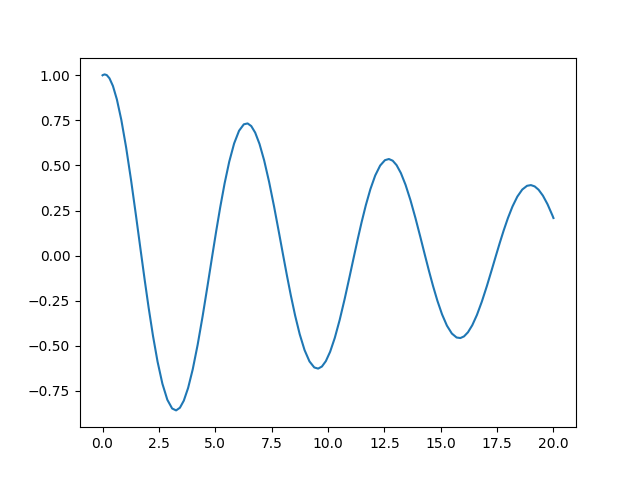
[<matplotlib.lines.Line2D object at 0x7fe1302b2ba0>]
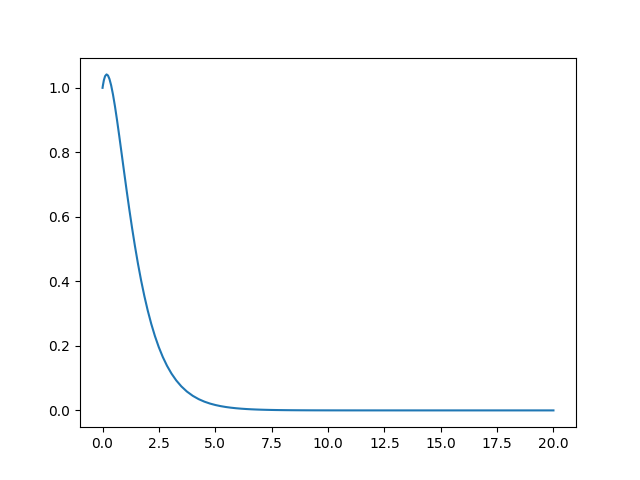
[<matplotlib.lines.Line2D object at 0x7fe13015aba0>]
plt.show()
Total running time of the script: (0 minutes 0.403 seconds)