Note
Go to the end to download the full example code.
Linear Covariance Analysis¶
This example is a simple implementation of linear covariance analysis [1] to evaluate closed-loop guidance, navigation, and control performance by propagating navigation errors and trajectory dispersions through a single simulation pass rather than simulating many realizations as in a Monte Carlo analysis.
We’ll use the Clohessy-Wiltshire equations to simulate the relative motion between a target vehicle in circular orbit and a chaser vehicle.
import casadi as ca
import numpy as np
import condor as co
from condor.backend import operators as ops
I6 = ops.eye(6)
Z6 = ops.zeros((6, 6))
W = ops.concat([I6, Z6], axis=0)
I3 = ops.eye(3)
Z3 = ops.zeros((3, 3))
V = ops.concat([Z3, I3, ops.zeros((6, 3))], axis=0)
The core of the analysis is an ODE system that represents the true state the follows the CW equations.
class LinCovCW(co.ODESystem):
omega = parameter()
scal_w = parameter(shape=6)
x = state(shape=6)
C = state(shape=(12, 12), symmetric=True)
initial[x] = parameter(shape=x.shape, name="initial_x")
initial[C] = parameter(shape=C.shape, name="initial_C")
# [0, 0, 0, 1, 0, 0],
# [0, 0, 0, 0, 1, 0],
# [0, 0, 0, 0, 0, 1],
# [0, 0, 0, 0, 0, 2*omega],
# [0, -omega**2, 0, 0, 0, 0],
# [0, 0, 3*omega**2, -2*omega, 0, 0]
Acw = ops.zeros((6, 6))
Acw[:3, 3:] = ops.eye(3)
Acw[3, 5] = 2 * omega
Acw[4, 1] = -(omega**2)
Acw[5, 2] = 3 * omega**2
Acw[5, 3] = -2 * omega
Scal_w = ops.diag(scal_w)
Cov_prop_offset = W @ Scal_w @ W.T
Fcal = ops.zeros((12, 12))
Fcal[:6, :6] = Acw
Fcal[6:, 6:] = Acw
dot[x] = Acw @ x
dot[C] = Fcal @ C + C @ Fcal.T + Cov_prop_offset
A discrete targeting maneuver can be implemented as an event on the ODE system that instantaneously updates the relative velocity as well as the augmented covariance.
class MajorBurn(LinCovCW.Event):
#: Target position
rd = parameter(shape=3)
#: Time ignition
tig = parameter()
#: Time end maneuver
tem = parameter()
scal_v = parameter(shape=3)
Delta_v_mag = state()
Delta_v_disp = state()
at_time = tig
td = tem - tig
stm = ops.zeros((6, 6))
stm[0, 0] = 1
stm[0, 2] = 6 * omega * td - 6 * ops.sin(omega * td)
stm[0, 3] = -3 * td + 4 * ops.sin(omega * td) / omega
stm[0, 5] = 2 * (1 - ops.cos(omega * td)) / omega
stm[1, 1] = ops.cos(omega * td)
stm[1, 4] = ops.sin(omega * td) / omega
stm[2, 2] = 4 - 3 * ops.cos(omega * td)
stm[2, 3] = 2 * (ops.cos(omega * td) - 1) / omega
stm[2, 5] = ops.sin(omega * td) / omega
stm[3, 2] = 6 * omega * (1 - ops.cos(omega * td))
stm[3, 3] = 4 * ops.cos(omega * td) - 3
stm[3, 5] = 2 * ops.sin(omega * td)
stm[4, 1] = -omega * ops.sin(omega * td)
stm[4, 4] = ops.cos(omega * td)
stm[5, 2] = 3 * omega * ops.sin(omega * td)
stm[5, 3] = -2 * ops.sin(omega * td)
stm[5, 5] = ops.cos(omega * td)
T_pp = stm[:3, :3]
T_pv = stm[:3, 3:]
T_pv_inv = ca.solve(T_pv, ops.eye(3))
Delta_v = (T_pv_inv @ rd - T_pv_inv @ T_pp @ x[:3, 0]) - x[3:, 0]
update[Delta_v_mag] = Delta_v_mag + ca.norm_2(Delta_v)
update[x] = x + ops.concat([ops.zeros((3, 1)), Delta_v])
DG = ca.vertcat(ops.zeros((3, 6)), ca.horzcat(-(T_pv_inv @ T_pp), -I3))
Dcal = ca.vertcat(
ca.horzcat(I6, DG),
ca.horzcat(Z6, I6 + DG),
)
Scal_v = ops.diag(scal_v)
update[C] = Dcal @ C @ Dcal.T + V @ Scal_v @ V.T
Mc = DG @ ops.concat([Z6, I6], axis=1)
sigma_Dv__2 = ca.trace(Mc @ C @ Mc.T)
update[Delta_v_disp] = Delta_v_disp + ca.sqrt(sigma_Dv__2)
A Terminating event at the end of the maneuver
class Terminate(LinCovCW.Event):
terminate = True
at_time = MajorBurn.tem
Trajectory analysis to simulate the system
class Sim(LinCovCW.TrajectoryAnalysis):
# TODO: add final burn Delta v (assume final relative v is 0, can get magnitude and
# dispersion)
tot_Delta_v_mag = trajectory_output(Delta_v_mag)
tot_Delta_v_disp = trajectory_output(Delta_v_disp)
# tf = parameter()
Mr = ca.horzcat(I3, ca.MX(3, 9))
sigma_r__2 = ca.trace(Mr @ C @ Mr.T)
final_pos_disp = trajectory_output(ca.sqrt(sigma_r__2))
Simulate
def make_C0(sigma_p, sigma_v, rho, sigma_p_nav=None, sigma_v_nav=None, rho_nav=None):
D0 = np.zeros((6, 6))
D0[:3, :3] = np.eye(3) * (sigma_p**2)
D0[2, 3] = rho * sigma_p * sigma_v
D0[3, 2] = rho * sigma_p * sigma_v
D0[3:, 3:] = np.eye(3) * (sigma_v**2)
sigma_p_nav = sigma_p_nav or sigma_p
sigma_v_nav = sigma_v_nav or sigma_v
rho_nav = rho_nav or rho
P0 = np.zeros((6, 6))
P0[:3, :3] = np.eye(3) * (sigma_p_nav**2)
P0[2, 3] = rho_nav * sigma_p_nav * sigma_v_nav
P0[3, 2] = rho_nav * sigma_p_nav * sigma_v_nav
P0[3:, 3:] = np.eye(3) * (sigma_v_nav**2)
C = np.concat(
(np.concat((D0, D0), axis=1), np.concat((D0, D0 + P0), axis=1)), axis=0
)
return C
initial_C = make_C0(100 / 3, 0.11 / 3, 0.9, 10 / 3, 0.011 / 3, 0.9)
sim_kwargs = dict(
omega=0.00114,
scal_w=[0.0] * 3 + [4.8e-10] * 3,
scal_v=[2.5e-7] * 3,
initial_x=[-2000.0, 0.0, 1000.0, 1.71, 0.0, 0.0],
initial_C=make_C0(100 / 3, 0.11 / 3, 0.9, 10 / 3, 0.011 / 3, 0.9),
rd=[500.0, 0.0, 0.0],
)
out = Sim(**sim_kwargs, tig=156.7, tem=156.7 + 15 * 60)
print(out.final_pos_disp)
[11.03987383]
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
def plot_traj(sim, x_idx=0, y_idx=2):
"""create relative motion plot in the vertical plane"""
fig, ax = plt.subplots(constrained_layout=True)
ax.invert_xaxis()
ax.set_xlabel("V-bar (m)")
ax.invert_yaxis()
ax.set_ylabel("R-bar (m)")
ax.grid(True)
ax.set_aspect("equal")
plt.xlim(1000, -2500)
plt.ylim(1500, -500)
fig.set_size_inches(7.4, 4.2)
sim_color = "C0"
plt.plot([0.0], [0.0], "ok")
xs = sim.x[x_idx].squeeze()
ys = sim.x[y_idx].squeeze()
ax.plot(xs, ys, "o-", color=sim_color)
ax.plot(xs[0], ys[0], "og")
n_std = 3
for pos_vel, cov in zip(sim.x.T.squeeze(), sim.C.T):
pos = pos_vel[[x_idx, y_idx]]
C = cov[[x_idx, y_idx]][:, [x_idx, y_idx]]
lambda_, v = np.linalg.eigh(C)
lambda_ = np.sqrt(lambda_)
ellipse = Ellipse(
pos,
width=lambda_[0] * n_std * 2,
height=lambda_[1] * n_std * 2,
angle=np.degrees(np.arctan2(*v[:, 0][::-1])),
edgecolor=sim_color,
facecolor="none",
)
ax.add_patch(ellipse)
return ax
plot_traj(out)
# TODO
# DV_idx = Sim.trajectory_output.flat_index(Sim.tot_Delta_v_mag)
# tig_idx = Sim.parameter.flat_index(Sim.tig)
# tem_idx = Sim.parameter.flat_index(Sim.tem)
# init_jac = Sim.implementation.callback.jac_callback(Sim.implementation.callback.p, [])
# print("init grad wrt tig", init_jac[DV_idx, tig_idx])
# print("init grad wrt tem", init_jac[DV_idx, tem_idx])
# """
# init grad wrt tig 0.0209833
# init grad wrt tem -0.0260249
# """
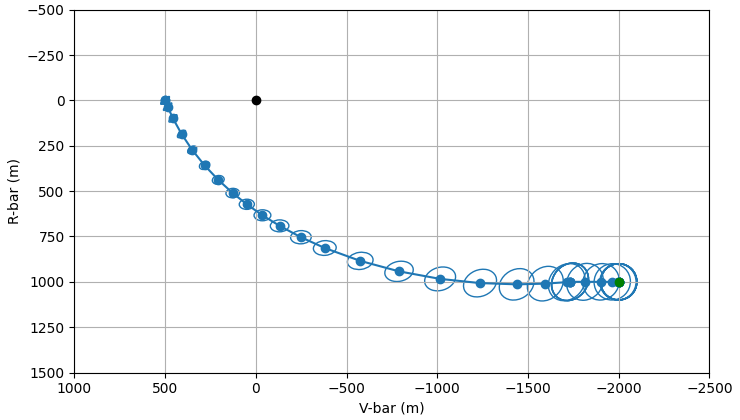
<Axes: xlabel='V-bar (m)', ylabel='R-bar (m)'>
class Hohmann(co.OptimizationProblem):
tig = variable(initializer=200.0)
tem = variable(initializer=500.0)
sim = Sim(tig=tig, tem=tem, **sim_kwargs)
objective = sim.tot_Delta_v_mag
constraint(tem > tig + 30)
constraint(tig > 0.1)
class Options:
# TODO
# __implementation__ = co.implementations.ScipyTrustConstr
exact_hessian = False
from time import perf_counter
hoh_start = perf_counter()
hohmann = Hohmann()
hoh_stop = perf_counter()
print(hohmann._stats)
print((hohmann.tem - hohmann.tig) * hohmann.sim.omega * 180 / np.pi)
# TODO
# opt_jac = Sim.implementation.callback.jac_callback(Sim.implementation.callback.p, [])
# print("opt grad wrt tig", opt_jac[DV_idx, tig_idx])
# print("opt grad wrt tem", opt_jac[DV_idx, tem_idx])
# """
# opt grad wrt tig -4.48258e-09
# opt grad wrt tem -1.47125e-09
# """
This is Ipopt version 3.14.19, running with linear solver MUMPS 5.8.2.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 3
Number of nonzeros in Lagrangian Hessian.............: 0
/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/casadi/casadi.py:913: FutureWarning:
casadi: a numpy function was called on a casadi value (issue #2959).
This used legacy casadi 3.7.2 behaviour, where the result type follows
the input:
- a numeric input (DM) -> a plain numpy array
- a symbolic input (SX / MX) -> a casadi value, or an error if the
function has no casadi equivalent
For a shape-correct, type-preserving result, opt in to the
casadi-aware numpy support:
try:
ca.GlobalOptions.setNumpyMode(1)
except AttributeError:
pass
Or use setNumpyMode(-1) to keep legacy behaviour silently.
Shown once; run python with -W always to see every occurrence.
_w.warn(_NUMPY_LEGACY_NOTICE, FutureWarning)
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 2
inequality constraints with only lower bounds: 2
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 6.4936391e+00 0.00e+00 2.60e-02 0.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 6.4925217e+00 0.00e+00 1.46e-02 -6.6 4.70e-02 - 9.90e-01 1.00e+00f 1
2 4.1522436e+00 0.00e+00 6.51e-03 -2.8 1.47e+02 - 9.84e-01 1.00e+00f 1
3 3.1748709e+00 0.00e+00 4.05e-03 -4.8 1.15e+02 - 1.00e+00 1.00e+00f 1
4 2.2263549e+00 0.00e+00 2.21e-03 -5.7 1.86e+02 - 1.00e+00 1.00e+00f 1
5 1.5484505e+00 0.00e+00 1.38e-03 -6.5 2.22e+02 - 1.00e+00 1.00e+00f 1
6 1.1046691e+00 0.00e+00 9.48e-04 -7.0 2.93e+02 - 1.00e+00 7.15e-01f 1
7 6.1851591e-01 0.00e+00 4.91e-04 -6.0 3.99e+02 - 4.14e-03 1.00e+00f 1
8 3.8428264e-01 0.00e+00 2.04e-04 -6.6 4.13e+02 - 1.00e+00 1.00e+00f 1
9 3.2279045e-01 0.00e+00 7.42e-05 -6.6 2.92e+02 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.9923153e-01 0.00e+00 4.12e-05 -7.6 2.44e+02 - 1.00e+00 1.00e+00f 1
11 2.8667982e-01 0.00e+00 1.61e-05 -11.0 3.09e+02 - 1.00e+00 1.00e+00f 1
12 2.8516474e-01 0.00e+00 4.61e-06 -8.4 9.54e+01 - 1.00e+00 1.00e+00f 1
13 2.8500540e-01 0.00e+00 7.76e-07 -9.4 3.64e+01 - 1.00e+00 1.00e+00f 1
14 2.8500011e-01 0.00e+00 1.72e-07 -11.0 8.69e+00 - 1.00e+00 1.00e+00f 1
15 2.8500003e-01 0.00e+00 9.59e-08 -11.0 7.39e-01 - 1.00e+00 1.00e+00f 1
16 2.8500000e-01 0.00e+00 5.46e-11 -11.0 2.81e-01 - 1.00e+00 1.00e+00f 1
Number of Iterations....: 16
(scaled) (unscaled)
Objective...............: 2.8500000000002501e-01 2.8500000000002501e-01
Dual infeasibility......: 5.4600501671383738e-11 5.4600501671383738e-11
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Variable bound violation: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 9.9999999167391719e-12 9.9999999167391719e-12
Overall NLP error.......: 5.4600501671383738e-11 5.4600501671383738e-11
Number of objective function evaluations = 17
Number of objective gradient evaluations = 17
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 17
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 17
Number of Lagrangian Hessian evaluations = 0
Total seconds in IPOPT = 3.639
EXIT: Optimal Solution Found.
{'iter_count': 16, 'iterations': {'alpha_du': [0.0, 0.9898285295685858, 0.9842402293561233, 1.0, 1.0, 1.0, 1.0, 0.00414002745213544, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], 'alpha_pr': [0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.7149778955620181, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], 'd_norm': [0.0, 0.04700771427236512, 147.03433930399902, 115.44642648213193, 186.41902166570998, 221.93260664117753, 292.95526879472163, 399.49156752563357, 413.03084327323984, 291.5653550257215, 244.33777326584067, 308.738537162242, 95.41495081529179, 36.415368027850974, 8.690722844633838, 0.7389692848732106, 0.28148098240419656], 'inf_du': [0.026024879059342105, 0.014605956528173522, 0.006505450906662369, 0.0040476207149815705, 0.0022089899534760834, 0.0013759448721080419, 0.0009482486871570577, 0.0004911213978947128, 0.00020364975153085266, 7.418601738923527e-05, 4.1238876683025756e-05, 1.6056230255729255e-05, 4.606922849928806e-06, 7.761787402380683e-07, 1.7195364506085692e-07, 9.587813836217483e-08, 5.460050167138374e-11], 'inf_pr': [0.0, 0.0, 0.0, 1.1368683772161603e-13, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 4.547473508864641e-13, 0.0, 0.0, 0.0, 0.0, 0.0, 4.547473508864641e-13], 'mu': [1.0, 2.3495000001000001e-07, 0.0014545402508683457, 1.5658669865843416e-05, 2.0938764474102797e-06, 3.1758246357024413e-07, 9.878583835826242e-08, 1.0564209599780559e-06, 2.5408340001332855e-07, 2.3511342127622884e-07, 2.6468653324647544e-08, 1e-11, 3.773980096222553e-09, 3.8985254757066545e-10, 1e-11, 1.0000000000000001e-11, 1e-11], 'obj': [6.493639138134979, 6.492521733862819, 4.152243602985165, 3.174870894093058, 2.226354873044947, 1.5484505240638509, 1.104669057376198, 0.6185159065516346, 0.38428263659658557, 0.32279044510894067, 0.29923152717882334, 0.28667982227554517, 0.2851647356025202, 0.28500540412278297, 0.2850001073857901, 0.2850000346414185, 0.285000000000025], 'regularization_size': [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]}, 'n_call_callback_fun': 0, 'n_call_nlp_f': 17, 'n_call_nlp_g': 17, 'n_call_nlp_grad': 0, 'n_call_nlp_grad_f': 18, 'n_call_nlp_jac_g': 18, 'return_status': 'Solve_Succeeded', 'success': True, 't_proc_callback_fun': 0.0, 't_proc_nlp_f': 1.1571200000000001, 't_proc_nlp_g': 0.00013700000000000002, 't_proc_nlp_grad': 0.0, 't_proc_nlp_grad_f': 6.70151, 't_proc_nlp_jac_g': 0.000177, 't_wall_callback_fun': 0.0, 't_wall_nlp_f': 0.5963384899999999, 't_wall_nlp_g': 0.000123473, 't_wall_nlp_grad': 0.0, 't_wall_nlp_grad_f': 3.026253251, 't_wall_nlp_jac_g': 0.00017421899999999998, 'unified_return_status': 'SOLVER_RET_SUCCESS'}
[179.99997662]
hohmann_sim = Sim(**sim_kwargs, tig=hohmann.tig, tem=hohmann.tem)
print(hohmann_sim.tot_Delta_v_disp)
print(hohmann_sim.final_pos_disp)
print(hohmann.tig, hohmann.tem)
print("time:", hoh_stop - hoh_start)
[93543.09060165]
[42980.59494175]
[84.09660115] [2839.87927261]
time: 3.671997637000004
plot_traj(hohmann_sim)
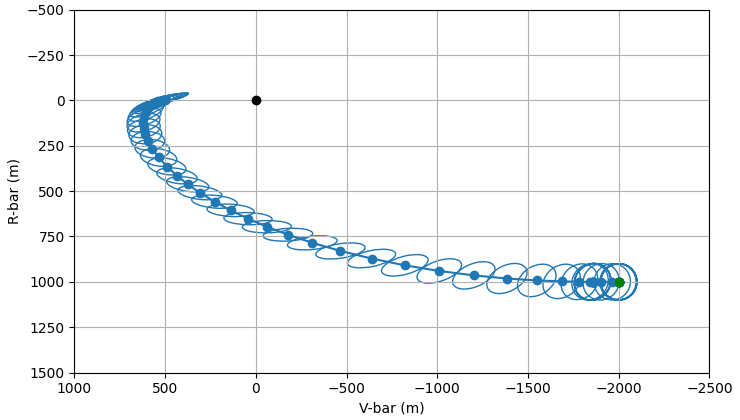
<Axes: xlabel='V-bar (m)', ylabel='R-bar (m)'>
class TotalDeltaV(co.OptimizationProblem):
tig = variable(initializer=200.0)
tem = variable(initializer=500.0)
constraint(tem - tig, lower_bound=30.0)
constraint(tig, lower_bound=0.0)
sim = Sim(tig=tig, tem=tem, **sim_kwargs)
# TODO: adding a parameter and constraint to existing problem SHOULD be done by
# inheritance... I suppose the originally Hohmann model could easily be written to
# include more parameters to solve all permutations of this problem... weights for
# each output, upper bounds for each output (and combinations?)
# what about including a default for a paremter at a model level? no, just make a
# dict like unbounded_kwargs to fill in with a large number/inf
pos_disp_max = parameter()
constraint(sim.final_pos_disp - pos_disp_max, upper_bound=0.0)
objective = sim.tot_Delta_v_mag + 3 * sim.tot_Delta_v_disp
class Options:
exact_hessian = False
total_delta_v = TotalDeltaV(pos_disp_max=1000)
This is Ipopt version 3.14.19, running with linear solver MUMPS 5.8.2.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 5
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 3
inequality constraints with only lower bounds: 2
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 7.1721180e+00 0.00e+00 2.79e-02 0.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 7.1707977e+00 0.00e+00 1.58e-02 -6.3 5.12e-02 - 9.90e-01 1.00e+00f 1
2 4.6314943e+00 0.00e+00 1.28e-02 -2.8 1.47e+02 - 9.99e-01 1.00e+00f 1
3 3.5748124e+00 0.00e+00 8.14e-03 -4.9 1.16e+02 - 9.99e-01 1.00e+00f 1
4 2.5573172e+00 0.00e+00 4.64e-03 -6.0 1.88e+02 - 1.00e+00 1.00e+00f 1
5 2.1303875e+00 0.00e+00 3.47e-03 -2.6 2.23e+02 - 1.00e+00 5.34e-01f 1
6 1.3896162e+00 0.00e+00 1.87e-03 -3.9 2.90e+02 - 7.65e-01 1.00e+00f 1
7 9.2343203e-01 0.00e+00 9.86e-04 -9.6 3.38e+02 - 5.86e-01 1.00e+00h 1
8 6.5880088e-01 0.00e+00 3.97e-04 -4.1 4.10e+02 - 1.00e+00 1.00e+00h 1
9 5.9556262e-01 0.00e+00 9.33e-05 -5.0 2.73e+02 - 9.70e-01 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 5.9214434e-01 0.00e+00 2.49e-05 -7.1 8.68e+01 - 1.00e+00 1.00e+00h 1
11 5.9201333e-01 0.00e+00 2.46e-06 -6.8 1.30e+01 - 9.99e-01 1.00e+00h 1
12 5.9200809e-01 0.00e+00 8.58e-07 -11.0 2.16e+00 - 1.00e+00 1.00e+00h 1
13 5.9200750e-01 0.00e+00 4.37e-09 -11.0 1.05e+00 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 13
(scaled) (unscaled)
Objective...............: 5.9200749529483099e-01 5.9200749529483099e-01
Dual infeasibility......: 4.3674765273095838e-09 4.3674765273095838e-09
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Variable bound violation: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 1.0003863375196739e-11 1.0003863375196739e-11
Overall NLP error.......: 4.3674765273095838e-09 4.3674765273095838e-09
Number of objective function evaluations = 14
Number of objective gradient evaluations = 14
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 14
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 14
Number of Lagrangian Hessian evaluations = 0
Total seconds in IPOPT = 4.451
EXIT: Optimal Solution Found.
tot_delta_v_sim = Sim(**sim_kwargs, tig=total_delta_v.tig, tem=total_delta_v.tem)
plot_traj(tot_delta_v_sim)
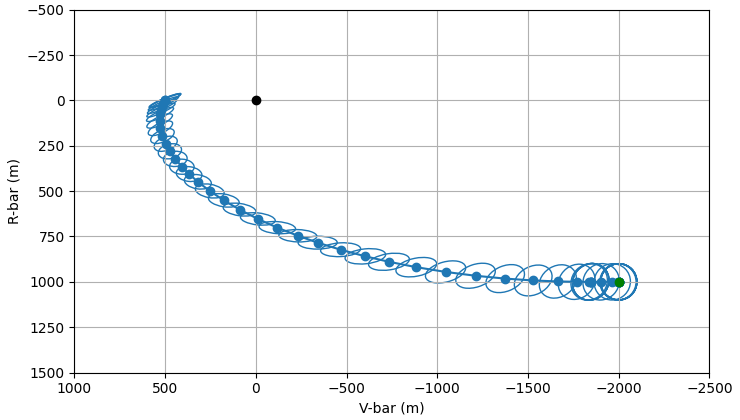
<Axes: xlabel='V-bar (m)', ylabel='R-bar (m)'>
total_delta_v_constrained = TotalDeltaV(pos_disp_max=10.0)
This is Ipopt version 3.14.19, running with linear solver MUMPS 5.8.2.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 5
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 3
inequality constraints with only lower bounds: 2
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 5.9200750e-01 2.16e+01 1.00e-03 0.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 5.9200750e-01 2.16e+01 2.14e+00 -6.1 2.16e+01 - 9.90e-01 4.58e-04h 1
2 1.2228222e+00 3.62e+00 7.92e-04 -1.2 9.87e+02 - 1.00e+00 1.00e+00h 1
3 1.7561268e+00 4.26e-01 1.00e-03 -2.5 2.71e+02 - 1.00e+00 1.00e+00h 1
4 1.8678722e+00 0.00e+00 1.40e-04 -2.5 4.38e+01 - 1.00e+00 9.99e-01h 1
5 1.8655032e+00 9.04e-05 2.26e-04 -3.7 8.88e-01 - 1.00e+00 9.83e-01h 1
6 1.8653259e+00 0.00e+00 4.41e-07 -9.8 1.48e-01 - 1.00e+00 1.00e+00h 1
Traceback (most recent call last):
File "/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/condor/backends/casadi/__init__.py", line 539, in eval
out = self.function(args[0])
^^^^^^^^^^^^^^^^^^^^^^
File "/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/condor/solvers/sweeping_gradient_method.py", line 1334, in __call__
return self.sweeping_gradient_method(self.trajectory_analysis.res)
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
File "/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/condor/solvers/sweeping_gradient_method.py", line 1215, in __call__
integrand_interp = make_interp_spline(
^^^^^^^^^^^^^^^^^^^
File "/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/scipy/interpolate/_bsplines.py", line 1869, in make_interp_spline
raise ValueError("The number of derivatives at boundaries does not "
ValueError: The number of derivatives at boundaries does not match: expected 2, got 0+0
Function jac_Sim_placeholder (0x562c970ceb10)
Input 0 (i0): [0.00114, 0, 0, 0, 4.8e-10, 4.8e-10, 4.8e-10, -2000, 0, 1000, 1.71, 0, 0, 1111.11, 0, 0, 0, 0, 0, 1111.11, 0, 0, 0, 0, 0, 0, 1111.11, 0, 0, 0, 0, 0, 1111.11, 0, 0, 0, 0, 0, 0, 1111.11, 1.1, 0, 0, 0, 0, 1111.11, 1.1, 0, 0, 0, 0, 1.1, 0.00134444, 0, 0, 0, 0, 1.1, 0.00134444, 0, 0, 0, 0, 0, 0, 0.00134444, 0, 0, 0, 0, 0, 0.00134444, 0, 0, 0, 0, 0, 0, 0.00134444, 0, 0, 0, 0, 0, 0.00134444, 1111.11, 0, 0, 0, 0, 0, 1122.22, 0, 0, 0, 0, 0, 0, 1111.11, 0, 0, 0, 0, 0, 1122.22, 0, 0, 0, 0, 0, 0, 1111.11, 1.1, 0, 0, 0, 0, 1122.22, 1.111, 0, 0, 0, 0, 1.1, 0.00134444, 0, 0, 0, 0, 1.111, 0.00135789, 0, 0, 0, 0, 0, 0, 0.00134444, 0, 0, 0, 0, 0, 0.00135789, 0, 0, 0, 0, 0, 0, 0.00134444, 0, 0, 0, 0, 0, 0.00135789, 500, 0, 0, -9.91538e-09, 954.339, 2.5e-07, 2.5e-07, 2.5e-07]
Input 1 (i1): [00, 00, 00]
Function fwd2_TotalDeltaV_constraint (0x562c971aff00)
Input 0 (i0): [-9.91538e-09, 954.339]
Input 1 (i1): 10
Input 2 (out_o0): [00, 00, 00]
Input 3 (fwd_i0):
[[1, 0],
[0, 1]]
Input 4 (fwd_i1): [[0, 0]]
Function nlp_jac_g (0x562c971ab3b0)
Input 0 (x): [-9.91538e-09, 954.339]
Input 1 (p): 10
CasADi - 2026-08-25 18:26:02 WARNING("IpoptUserClass::eval_jac_g failed:.../casadi/core/oracle_function.cpp:367: Error in TotalDeltaV_optimizer:nlp_jac_g:Error in Function::operator() for 'nlp_jac_g' [MXFunction] at .../casadi/core/function.cpp:1736:
Error in Function::operator() for 'fwd2_TotalDeltaV_constraint' [MXFunction] at .../casadi/core/function.cpp:1736:
Error in Function::operator() for 'jac_Sim_placeholder' [CallbackInternal] at .../casadi/core/function.cpp:1736:
.../casadi/core/function_internal.cpp:4010: Failed to evaluate 'eval_dm' for jac_Sim_placeholder:
.../casadi/core/callback_internal.cpp:116: Error calling "eval" for object jac_Sim_placeholder:
/work/swig/python/target3/source/casadiPYTHON_wrap_gil_release.cxx:4448: The number of derivatives at boundaries does not match: expected 2, got 0+0") [.../casadi/interfaces/ipopt/ipopt_nlp.cpp:159]
Number of Iterations....: 6
Number of objective function evaluations = 8
Number of objective gradient evaluations = 7
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 8
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 8
Number of Lagrangian Hessian evaluations = 0
Total seconds in IPOPT = 2.492
EXIT: Invalid number in NLP function or derivative detected.
tot_delta_v_constrained_sim = Sim(
**sim_kwargs, tig=total_delta_v_constrained.tig, tem=total_delta_v_constrained.tem
)
plot_traj(tot_delta_v_constrained_sim)
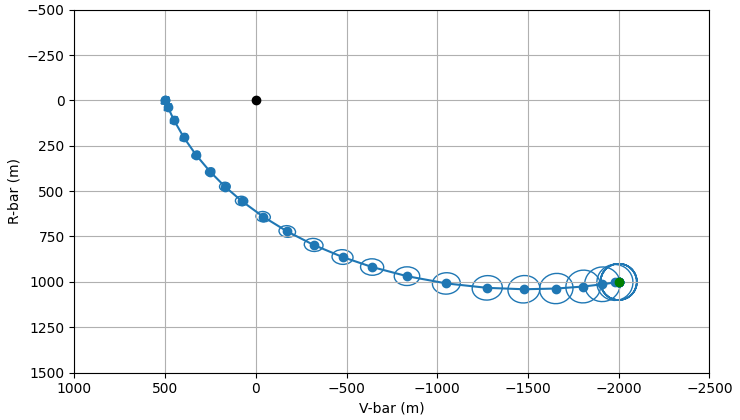
<Axes: xlabel='V-bar (m)', ylabel='R-bar (m)'>
print("\n" * 2, "unconstrained Delta v")
print(total_delta_v._stats)
print((total_delta_v.tem - total_delta_v.tig) * total_delta_v.sim.omega * 180 / np.pi)
print(tot_delta_v_sim.final_pos_disp)
print("\n" * 2, "constrained Delta v")
print(total_delta_v_constrained._stats)
print(
(total_delta_v_constrained.tem - total_delta_v_constrained.tig)
* total_delta_v_constrained.sim.omega
* 180
/ np.pi
)
print(tot_delta_v_constrained_sim.final_pos_disp)
plt.show()
unconstrained Delta v
{'iter_count': 13, 'iterations': {'alpha_du': [0.0, 0.9898141549346541, 0.9989278174798406, 0.9990960213085411, 1.0, 1.0, 0.764859696440671, 0.5862474784081376, 1.0, 0.9697500890809372, 1.0, 0.9992803183405823, 0.9997307924358011, 1.0], 'alpha_pr': [0.0, 1.0, 1.0, 1.0, 1.0, 0.5339668186918952, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], 'd_norm': [0.0, 0.05118226403964431, 147.31055370906643, 115.90309637851425, 187.7307422406867, 222.85632685767234, 289.9825004267386, 338.1023341473806, 410.306257902587, 272.99660059369467, 86.75140268815748, 13.026263618109919, 2.1579846814226635, 1.0512703158589183], 'inf_du': [0.02790119311111404, 0.01581519455934119, 0.012774754882012997, 0.008137855209943333, 0.004635016915627503, 0.003468381772670841, 0.0018650199910763012, 0.0009862330287146099, 0.00039688067974137685, 9.334584411960278e-05, 2.49109417901164e-05, 2.4601049479227312e-06, 8.583286196168886e-07, 4.367476527309584e-09], 'inf_pr': [0.0, 4.360686034488026e-09, 0.03827253453391677, 0.028469932938492093, 0.09160001786904104, 0.09143869225101753, 0.5046905688559491, 0.6542199968343994, 0.816749143628499, 0.26204794648981533, 0.014750287880588075, 7.302733024516783e-05, 1.0747302781055623e-05, 2.5203039513144176e-06], 'mu': [1.0, 4.877296677568146e-07, 0.0014972410914916795, 1.3109105651093222e-05, 9.418225541706308e-07, 0.0024587055752336097, 0.00012123606688098666, 2.471028001410016e-10, 8.115076356397787e-05, 1.0059392256430777e-05, 7.41646391065408e-08, 1.7263629774743278e-07, 1e-11, 1e-11], 'obj': [7.17211796170742, 7.170797695051909, 4.631494345636004, 3.5748124184966157, 2.5573171734478604, 2.130387503896834, 1.3896162137529753, 0.923432034254794, 0.6588008797889643, 0.59556262210967, 0.5921443437405741, 0.5920133330973234, 0.5920080922567437, 0.592007495294831], 'regularization_size': [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]}, 'n_call_callback_fun': 0, 'n_call_nlp_f': 14, 'n_call_nlp_g': 14, 'n_call_nlp_grad': 0, 'n_call_nlp_grad_f': 15, 'n_call_nlp_jac_g': 15, 'return_status': 'Solve_Succeeded', 'success': True, 't_proc_callback_fun': 0.0, 't_proc_nlp_f': 0.0011279999999999999, 't_proc_nlp_g': 1.185287, 't_proc_nlp_grad': 0.0, 't_proc_nlp_grad_f': 4.732149, 't_proc_nlp_jac_g': 5.421777999999999, 't_wall_callback_fun': 0.0, 't_wall_nlp_f': 0.0011347969999999999, 't_wall_nlp_g': 0.41422052800000003, 't_wall_nlp_grad': 0.0, 't_wall_nlp_grad_f': 2.028419377, 't_wall_nlp_jac_g': 1.9971898170000002, 'unified_return_status': 'SOLVER_RET_SUCCESS'}
[141.41273551]
[31.59576929]
constrained Delta v
{'iter_count': 6, 'iterations': {'alpha_du': [0.0, 0.9900018897466567, 1.0, 1.0, 1.0, 1.0, 0.999626801324771], 'alpha_pr': [0.0, 0.00045823297932979596, 1.0, 1.0, 0.9994939097396214, 0.9830114661836095, 1.0], 'd_norm': [0.0, 21.604730446245004, 987.217490713779, 270.6040624438334, 43.78435212260434, 0.8878344783499733, 0.14759632249447122], 'inf_du': [0.001, 2.137965788523387, 0.0007916273282377698, 0.0010007425505620463, 0.00014046967836967494, 0.00022595313033768605, 4.4122131478366994e-07], 'inf_pr': [21.605769282248097, 21.595868806220935, 3.6514809612995154, 0.4285153390118931, 0.011711473029754851, 0.00020366157085676545, 1.2360222313369154e-07], 'mu': [1.0, 7.416902494414036e-07, 0.07074735738619559, 0.003465880626531299, 0.003538171854825831, 0.0002003938970854395, 1.4496311779105657e-10], 'obj': [0.592007495294831, 0.5920074952949033, 1.2228221875157421, 1.7561267951797406, 1.8678722377365484, 1.8655031925456118, 1.8653259329111678], 'regularization_size': [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]}, 'n_call_callback_fun': 0, 'n_call_nlp_f': 8, 'n_call_nlp_g': 8, 'n_call_nlp_grad': 0, 'n_call_nlp_grad_f': 8, 'n_call_nlp_jac_g': 9, 'return_status': 'Invalid_Number_Detected', 'success': False, 't_proc_callback_fun': 0.0, 't_proc_nlp_f': 0.000688, 't_proc_nlp_g': 0.584748, 't_proc_nlp_grad': 0.0, 't_proc_nlp_grad_f': 2.619992, 't_proc_nlp_jac_g': 3.1024349999999994, 't_wall_callback_fun': 0.0, 't_wall_nlp_f': 0.000691267, 't_wall_nlp_g': 0.199151792, 't_wall_nlp_grad': 0.0, 't_wall_nlp_grad_f': 1.106490993, 't_wall_nlp_jac_g': 1.179939249, 'unified_return_status': 'SOLVER_RET_UNKNOWN'}
[62.33473822]
[10.00000019]
References
Total running time of the script: (0 minutes 11.560 seconds)