Condor Design¶

Overall goals and API¶

Condor is a new mathematical modeling framework for Python, developed at NASA’s Ames Research Center. Initial development began in April 2023 to address model implementation challenges for aircraft synthesis and robust orbital trajectory design. Condor emphasizes modern approaches from the scientific python community, and leverages many open-source software packages to expedite development and ensure robust and efficient run-time.

The goal is for Condor to help evaluate numerical models and then get out of the way. One key aspect to achieve this goal was to create an API that looked as much like the mathematical description as possible with as little distraction from programming cruft as possible. For example, Sellar [sellar] introduces an arbitrary system of algebraic equations to represent coupling in multi-disciplinary analysis,

\begin{array}{r} \begin{aligned} y_{1} & = x_{0}^{2} + x_{1} + x_{2} - 0.2 y_{2} \\ y_{2} & = \sqrt{y_{1}} + x_{0} + x_{1} \end{aligned} \end{array}

should be writable as

y1 == x[0] ** 2 + x[1] + x[2] - 0.2 * y2
y2 == y1**0.5 + x[0] + x[1]

Of course, in both the mathematical and programmatic description, the source of each symbol must be defined. In an engineering memo, we might say “where $y_{1}, y_{2}$ are the variables to solve and $x \in R^{3}$ parameterizes the system of equations,” which suggests the API for an algebraic system of equations as

import condor as co
class Coupling(co.AlgebraicSystem):
    x = parameter(shape=3)
    y1 = variable(initializer=1.)
    y2 = variable(initializer=1.)

    residual(y1 == x[0] ** 2 + x[1] + x[2] - 0.2 * y2)
    residual(y2 == y1**0.5 + x[0] + x[1])

which can be evaluated by instantiating the model with numerical values for the parameter, which binds the result from the iterative solver to the named element and field attributes on model instance, by calling the model,

coupling = Coupling([5., 2., 1]) # evaluate the model numerically
print(coupling.y1, coupling.y2) # individual elements are bound numerically
print(coupling.variable) # fields are bound as a dataclass

This pythonic data structure allows Condor to be integrated into larger analysis workflows with as little Condor-specific coding as possible.

Condor uses metaprogramming to to turn the class declaration mechanism into a blackboard-like environment to achieve the desired API. This approach helps us see these mathematical models as data structures that can then be transformed as needed to automate the process that is typically performed manually for defining and evaluating mathematical models in engineering analysis,

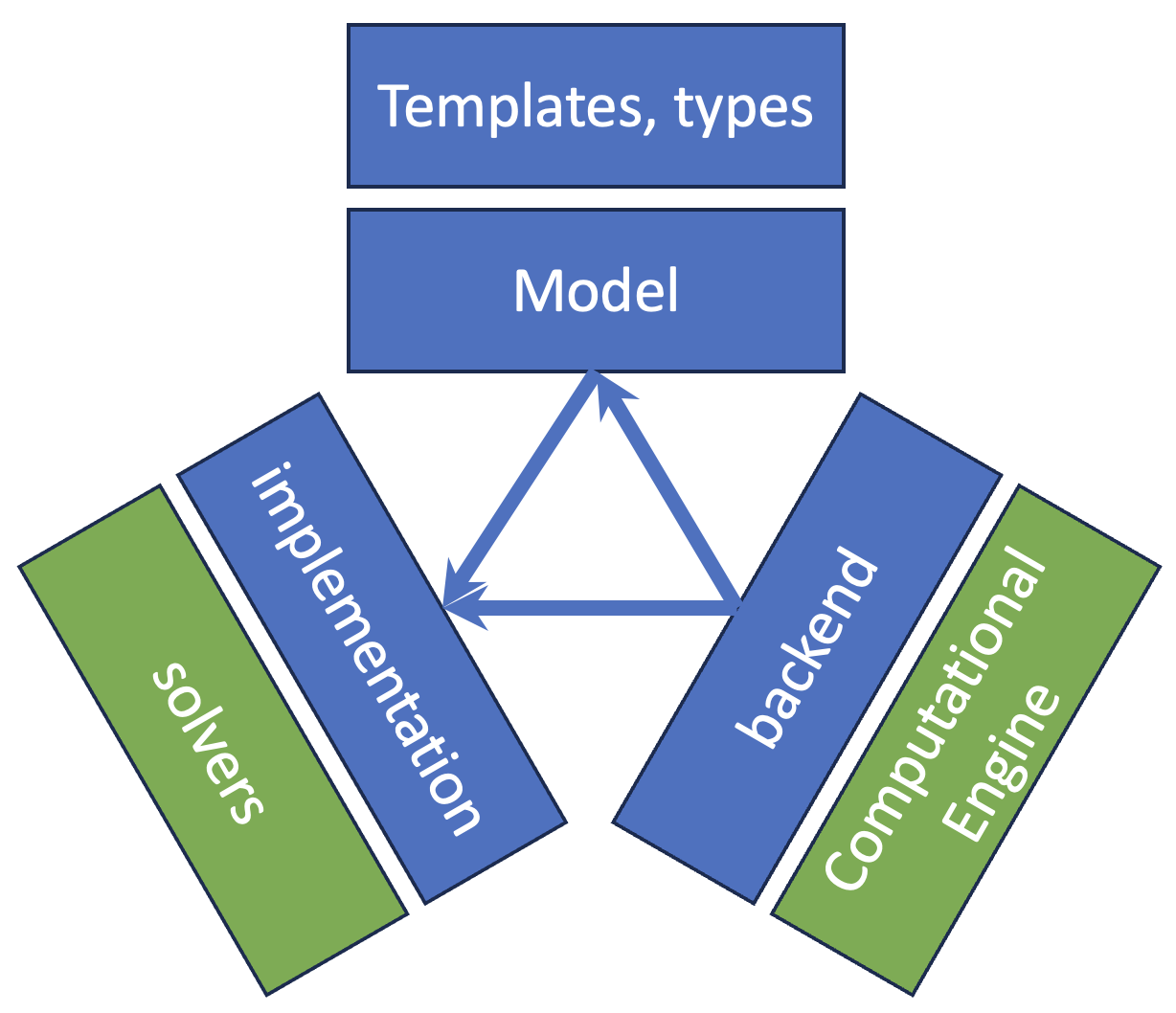
Architecture¶

We followed modern pythonic best-practices and patterns to settle on a multi-layered architecture like the Model-View-Controller paradigm in web development. The three key components of the architecture are:

The model layer, which provides an API for users to write their model. Condor models are ultimately a data structure which represents the represents the user’s mathematical intent for the model.
The backend layer provides a consistent interface to a third party Computational Engine, a symbolic-computational library which provides symbolic representation of elements and operations with awareness for basic differential calculus. The goal for the backend is provide a thin wrapper with a consistent interface so the computational engine implementation could be swapped out. Currently, we ship with CasADi as the only engine, although we hope to demonstrate a backend module for an alternate backend in the future.
The implementation layer is the glue code that operates on the model data structure, using the backend to form the numerical functions needed to call the third-party solvers which implement the nuemrical algorithms of interest. The implementation layer then calls the solver and binds the results to the model instance.

The Model Layer¶

Each user model is declared as a subclass of a Model Template, a class with a ModelType metaclass, which defines the fields from which elements are drawn to define the model. Condor currently ships with 5 model templates:

built-in template	fields
built-in template	input	internal	output
`ExplicitSystem`	input		output
`TableLookup`	input	input_data output_data	output
`AlgebraicSystem`	parameter	residual	variable output
`TrajectoryAnalysis`	parameter	state modal.action	trajectory_output
`OptimizationProblem`	parameter	objective constraint	variable

Models can be used recursively, building up more sophisticated models by embedding models within another. However, system encapsulation is enforced so only elements from input and output fields are accessible after the model has been defined. For example, we may wish to optimize Sellar’s algebraic system of equations. Mathematically, we can define the optimization as

\begin{array}{r} \begin{aligned} \underset{x \in R^{3}}{minimize} & x_{2}^{2} + x_{1} + y_{1} + e^{- y_{2}} \\ subject to & 3.16 \leq y_{1} \\ y_{2} \leq 24.0 \end{aligned} \end{array}

where $y_{1}$ and $y_{2}$ are the solution to the system of algebraic equations described above. In condor, we can write this as

from condor import operators as ops
class Sellar(co.OptimizationProblem):
    x = variable(shape=3, lower_bound=0, upper_bound=10)
    coupling = Coupling(x)
    y1, y2 = coupling

    objective = x[2]**2 + x[1] + y1 + ops.exp(-y2)
    constraint(y1 > 3.16)
    constraint(24. > y2)

As with the system of algebraic equations, we can numerically solve this optimization problem by providing an initial value for the variables and instantiating the model. The resulting object will have a dot-able data structure with the bound results, including the embedded Coupling model:

Sellar.set_initial(x=[5,2,1])
sellar = Sellar()
print()
print("objective value:", sellar.objective) # scalar value
print(sellar.constraint) # field
print(sellar.coupling.y1) # embedded-model element

The built-in model types provide a useful library to build small or one-off modeling capabilities. We also ensured that there were good mechanisms for customizing models and creating new models to address repeat and sophisticated modeling tasks.

Fields and Elements¶

A model template defines what fields are available to organize expressions to represent a particular mathematical model. Different field types are used for different purposes:

FreeField: used to represent independent leaf expressions, typically used as function inputs to solver callbacks
MatchedField: used to define expressions that correspond to elements from another field, for example initial conditions and time derivatives in ODESystem are matched to state, a FreeField
AssignedField: used to represent assigned expressions, often outputs of models

User models then draw elements from (free) fields and define expressions for the matched and assigned fields.

Metaprogramming class declaration¶

Ionel provides a nice overview of the Python 3 process for class declaration and object instantiation. Relevant for us is the following call order. For class declaration,

Metaclass.__prepare__() creates a class dictionary at the entry of the class declaration.
Each assignment within the class declaration uses the __setitem__() of the class dictionary
Metaclass.__new__() is passed the (filled) class dictionary and creates the class via type.__call__(). Note that Metaclass.__init__() is also called after this but is not as useful because the class is already fully constructed by this point; the __init__ can only be used to organize post-processing.

In Condor, the BaseModelType provides a common base metaclass for model template and user model classes. An outline of the key method calls:

__prepare__()
1. prepare_create() to create the custom (over-writable) dictionary, cls.dict_class
2. prepare_populate() to perform the condor-specific inheritance process (iterating over bases and calling inherit_item())
__new__()
1. separate condor related attributes from non-condor attributes
2. call super().__new__() with non-condor attributes
3. cls.process_fields() for preparing fields and their elements for processing
4. iterate over condor-related attributes, and call cls.process_condor_attrs(), which at this point primarily attaches elements and nothing else

In both __prepare__() and __new__(), steps are taken to determine if a ModelTemplate or Model is being declared, and manipulations to the inheritance tree are made appropriately. There are three cases:

Template declaration define the fields, etc that user code will create
class Model declaration create the class from the template that user models will inherit “base model for inheritance”
user model declaration inherits from template (or another use model), but creates a subclass of Model

There are essentially two types of inheritance.

Condor inheritance works by traversing the MRO and directly copying or creating a reference to the subclass
Python inheritance which looks to the class to find an attribute, and if not found, checks each class in the MRO until it is found (or raises an exception)

`ModelTemplate` declaration¶

ModelTemplateType is responsible for dispatching to the appropriate metaclass, and performs more pre-processing to handle several additional flags:

as_template: used to define abstract base models (particularly useful to deploy placeholder field elements)
model_metaclass: used to assign a metaclass for user models to add model-specific processing, including the specification of a custom dictionary or metadata class.
placeholder: an injected field used to declare singleton keywords

`Model` declaration¶

ModelType makes the following changes to BaseModelType's process:

in prepare_populate(), handles custom metadata class creation and injects dynamic_link
in __new__(),
1. dispatch appropriately if this is the creation of the class that user models will be assigned OR this is a user model
2. call super().__new__() to run BaseModelType's process
3. update docstring
4. inherit submodel templates
5. inherit_template_methods() copies class and instance methods as appropriate; unfortunately since Condor inheritance must be used, which breaks standard Python inheritance, super() cannot be used directly in user methods.
6. process_placeholders() collects the placeholder values and substitutes them into existing expressions
7. bind_model_fields() creates the dataclasses for each field

The last two steps are particularly useful hooks to customize behavior in a custom model metaclass.

Calling and binding¶

In Python, an instance of a class is created when the __class__ is __call__()ed,

calls the __new__() with any args and kwargs, which creates the self object
calls the __init__() with the self object and any args and kwargs

The condor.Model.__init__() has the following process:

bind_input_fields() which uses staticmethod function_call_to_fields() to parse the positional and keyword arguments to bind the values for the input field(s)
classmethod get_implementation_class() finds the implementation class and create an instance
evalaute the implementation which is responsible for binding the output fields
bind_embedded_models() recursive evaluates and binds embedded models, if the metadata flag is true

In some instance-creation routines, like OptimizaitonProblem's from_values(), it is useful to use __new__() on the model directly to bypass the standard __init__() processing described here.

The implementation layer¶

The implementation layer is responsible for using the backend to create the numerical functions needed to evaluate model and call any solvers as needed.

The embedded Options class inside a model provides a name-space for specifying solver options. Attributes without a leading underscore can be placed into a dict by condor.implementations.utils.options_to_kwargs() to pass to the solver. The __implementation__ is used to specify the class to use, otherwise inheriting from the template.

Due to initial coupling with the casadi computational engine, the contrib model implementations follow a pattern of calling

construct() to create the callables from the model fields and setup the solver
__call__() to run the solver and bind the output fields

Ultimately it is the implementation’s job to parse the Options. The intention is to make the argument manipulation at the implementation layer as thin as possible. This is not always possible, especially when supporting multiple solvers for the same model template.

The Options can be considered model inputs that make sense to have a default. They are also intended to be inputs that don’t define the mathematical meaning of the model.

The backend¶

The backend layer provides a common interface to potential “computational engine” libraries. Currently, we support only the CasADi engine. Condor uses a “shim” so that the capability needed by the computational engine can be accessed from the same import within the library. For each engine, a backends module must be provided to adapt the engine to a common API.

Using Condor for a “tool” or library¶

Useful engineering analysis tools can be built as a Python library simply by constructing the desired model with the contrib models. Since the Model is defined by constructing a class, Python class variable scoping prevents the dynamic definition of models inside a factory function. To get around this, a “configuration” pattern was defined with a dynamic_link() helper. The Systems Analysis Office at NASA’s Ames Research Center has used this approach to build an aircraft synthesis and analysis tool using Condor.

More recently, the metaprogramming back-bone of Condor was refactored to facilitate the customization of symbolic processing to facilitate the creation of custom ModelTemplates. To create a new type of analysis tool, we now recommend leveraging this capability. A design process might include:

Identify the data required to specify the analysis, and identify the Field (or create a custom Field) that would be appropriate for holding that data

Identify (or create) what solver and implementation is needed, including a mapping from the new type of Model to an existing model or solver.

Implement a process_placeholder() for processing the models data so the implementation can call the solver.

References

[sellar]

Sellar, R., Batill, S., and Renaud, J., “Response Surface Based, Concurrent Subspace Optimization for Multidisciplinary System Design,” 1996. https://doi.org/10.2514/6.1996-714