Confidence Interval

A novel technique is to calculate a differentiable confidence interval. This technique is specifically implemented for use with OpenMDAO and is not used elsewhere in the UQPCE package to calculate confidence intervals. See the section about derivatives for more information on why this approach is used.

Technique

(14)\[ f(\vec{y}, z, \mu) = 1 - \frac{1+tanh(\frac{\vec{y}-z}{\mu})}{2} \]

First, an initial guess of the uncertainty interval is chosen by interpolating the resampled data. The activation function is evaluated at this value of \(z\) for all \(y\), and the sum of the activation outputs is taken.

For any given problem, we know that the desired bound is either \(a=\frac{sig}{2}\) or \(a=1-\frac{sig}{2}\) for lower bound and upper bound, respectively. Because of this, we drive the residual in the below equation to zero

(15)\[ \mathcal{R} = a - \frac{\sum_{i=1}^{N} f(y_i, z, \mu)}{N} \]

Once the residual is driven to \(0\), the corresponding \(z\) is the location of the desired uncertainty interval.

Example

A standard normal distribution is used to demonstrate solving for the uncertainty interval from a set of responses. As a standard normal distribution, we know that the upper 95% uncertainty interval is located at 1.96; with this in mind, we will walk through three steps to show how this uncertainty interval is found.

Click to collapse visual

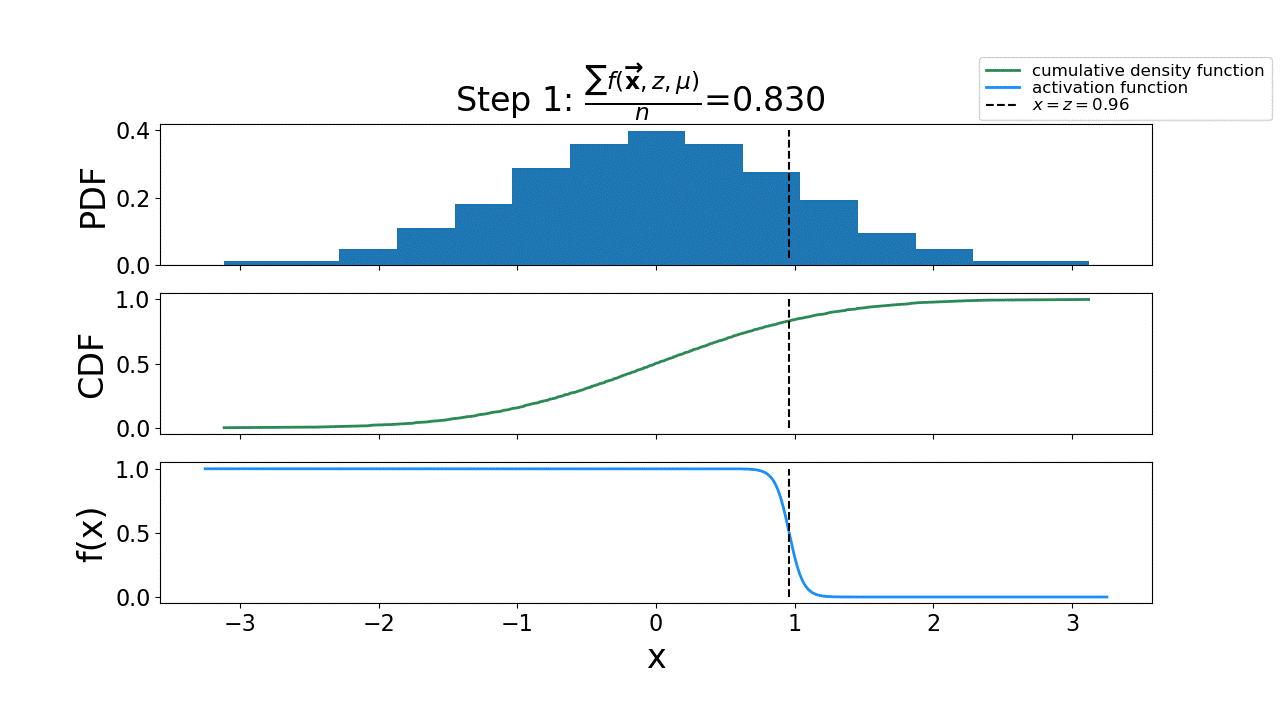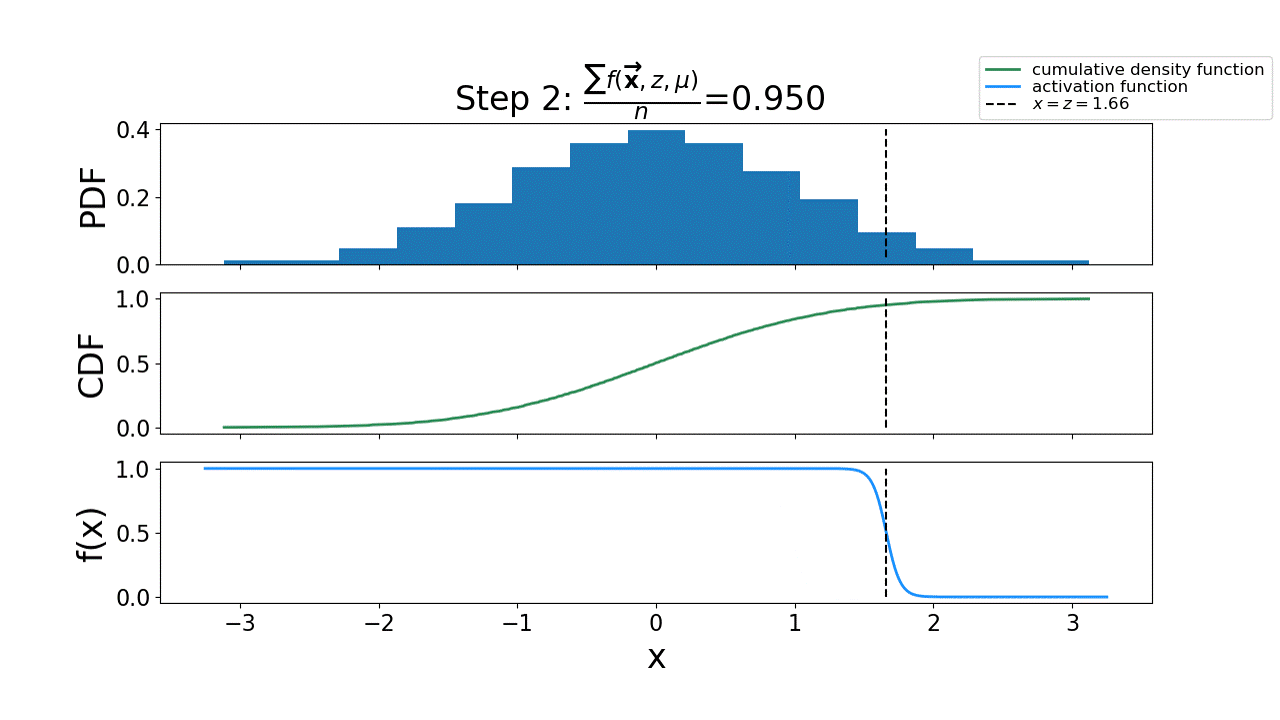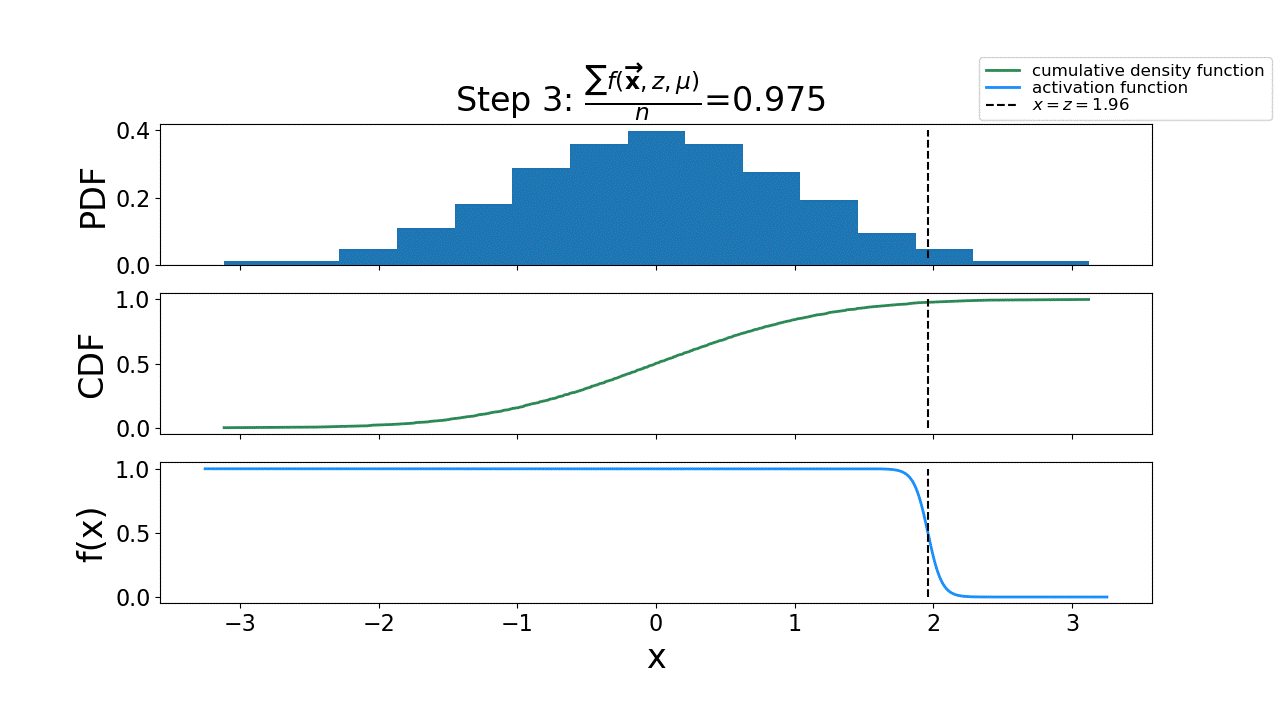
Fig. 14 The process of using the activation function to solve for the uncertainty interval by driving the residual to \(0\).

1. An initial guess, \(z=0.96\), is used. This leads to \(\frac{\sum_{i=1}^{N} f(y_i, z, \mu)}{N}=0.830\), making the residual \(\mathcal{R} = 0.975-0.830 = 0.145\)

2. The next step has \(z=1.66\), where \(\frac{\sum_{i=1}^{N} f(y_i, z, \mu)}{N}=0.950\), making the residual \(\mathcal{R} = 0.975-0.950 = 0.025\)

3. The final step chooses \(z=1.96\), where \(\frac{\sum_{i=1}^{N} f(y_i, z, \mu)}{N}=a=0.975\), which makes the residual \(\mathcal{R} \approx 0\)