Functionalizing a Modeled Dataset¶
This section demonstrates the four syntax options for functionalizing a modeled dataset. For a list of model outputs currently supported by Kamodo, visit the 'Choosing a Model and Variable' section.
Important!
- If you decide to add or remove data from the chosen file directory, you must remove the TIEGCM_list.txt and TIEGCM_times.txt files from the same directory and rerun the above command. The name changes with the model name (e.g. WACCMX_list.txt and WACCMX_times.txt for the WACCMX model, and so on).
Import the model-specific model reader object.¶
In [2]:
Copied!
import kamodo_ccmc.flythrough.model_wrapper as MW
file_dir = 'D:/GITM/jasoon_shim_071418_IT_1_tenth_oneday/'
reader = MW.Model_Reader('GITM')
import kamodo_ccmc.flythrough.model_wrapper as MW
file_dir = 'D:/GITM/jasoon_shim_071418_IT_1_tenth_oneday/'
reader = MW.Model_Reader('GITM')
In [5]:
Copied!
# The documentation for all the readers is mostly the same.
# Some have unique components based on the custom logic required in those cases.
reader.__doc__.split('\n')
# The documentation for all the readers is mostly the same.
# Some have unique components based on the custom logic required in those cases.
reader.__doc__.split('\n')
Out[5]:
['GITM model data reader.', '', ' Inputs:', ' file_dir: a string representing the file directory of the', ' model output data.', " Note: This reader 'walks' the entire dataset in the directory.", ' variables_requested = a list of variable name strings chosen from', ' the model_varnames dictionary in this script, specifically the', ' first item in the list associated with a given key.', ' - If empty, the reader functionalizes all possible variables', ' (default)', " - If 'all', the reader returns the model_varnames dictionary", ' above for only the variables present in the given files.', ' filetime = boolean (default = False)', ' - If False, the script fully executes.', ' - If True, the script only executes far enough to determine the', ' time values associated with the chosen data.', ' printfiles = boolean (default = False)', ' - If False, the filenames associated with the data retrieved', ' ARE NOT printed.', ' - If True, the filenames associated with the data retrieved ARE', ' printed.', ' gridded_int = boolean (default = True)', ' - If True, the variables chosen are functionalized in both the', ' standard method and a gridded method.', ' - If False, the variables chosen are functionalized in only the', ' standard method.', ' verbose = boolean (False)', ' - If False, script execution and the underlying Kamodo', ' execution is quiet except for specified messages.', ' - If True, be prepared for a plethora of messages.', ' All inputs are described in further detail in', ' KamodoOnboardingInstructions.pdf.', '', ' Returns: a kamodo object (see Kamodo core documentation) containing all', ' requested variables in functionalized form.', ' ']
Default functionalization method¶
In [3]:
Copied!
# This default function call functionalizes all the variables in the data,
# including gridded versions for visualization.
# TIEGCM has a data type error due to a file creation error.
kamodo_object_default = reader(file_dir) # (gridded_int=True is default)
kamodo_object_default
# This default function call functionalizes all the variables in the data,
# including gridded versions for visualization.
# TIEGCM has a data type error due to a file creation error.
kamodo_object_default = reader(file_dir) # (gridded_int=True is default)
kamodo_object_default
Out[3]:
\begin{equation}\operatorname{SZA}{\left(\vec{r}_{GDZsph3D} \right)}[radians] = \lambda{\left(\vec{r}_{GDZsph3D} \right)}\end{equation} \begin{equation}\operatorname{SZA_{ijk}}(time[hr],lon[deg],lat[deg])[radians] = \lambda{\left(time,lon,lat \right)}\end{equation} \begin{equation}\operatorname{SLT}{\left(\vec{r}_{GDZsph3D} \right)}[hr] = \lambda{\left(\vec{r}_{GDZsph3D} \right)}\end{equation} \begin{equation}\operatorname{SLT_{ijk}}(time[hr],lon[deg],lat[deg])[hr] = \lambda{\left(time,lon,lat \right)}\end{equation} \begin{equation}\operatorname{TEC}{\left(\vec{r}_{GDZsph3D} \right)}[\frac{10000000000000000}{m^{2}}] = \lambda{\left(\vec{r}_{GDZsph3D} \right)}\end{equation} \begin{equation}\operatorname{TEC_{ijk}}(time[hr],lon[deg],lat[deg])[\frac{10000000000000000}{m^{2}}] = \lambda{\left(time,lon,lat \right)}\end{equation} \begin{equation}\rho_{N2}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{N2 ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{N2+}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{N2+ ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{NO}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{NO ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{NO+}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{NO+ ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{O2}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O2 ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{O2+}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O2+ ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{O3P}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O3P ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{O+4S4P}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O+4S4P ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\rho_{n}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{n ijk}(time[hr],lon[deg],lat[deg],height[km])[\frac{kg}{m^{3}}] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{T_{n}}{\left(\vec{r}_{GDZsph4D} \right)}[K] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{T_{n ijk}}(time[hr],lon[deg],lat[deg],height[km])[K] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{v_{ieast}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{ieast ijk}}(time[hr],lon[deg],lat[deg],height[km])[m / s] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{v_{inorth}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{inorth ijk}}(time[hr],lon[deg],lat[deg],height[km])[m / s] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{v_{iup}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{iup ijk}}(time[hr],lon[deg],lat[deg],height[km])[m / s] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{v_{neast}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{neast ijk}}(time[hr],lon[deg],lat[deg],height[km])[m / s] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{v_{nnorth}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{nnorth ijk}}(time[hr],lon[deg],lat[deg],height[km])[m / s] = \lambda{\left(time,lon,lat,height \right)}\end{equation} \begin{equation}\operatorname{v_{nup}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{nup ijk}}(time[hr],lon[deg],lat[deg],height[km])[m / s] = \lambda{\left(time,lon,lat,height \right)}\end{equation}
Functionalization method 1¶
Functionalize all variables, excluding the gridded versions.
In [4]:
Copied!
kamodo_object_1 = reader(file_dir, gridded_int=False)
kamodo_object_1
kamodo_object_1 = reader(file_dir, gridded_int=False)
kamodo_object_1
Out[4]:
\begin{equation}\operatorname{SZA}{\left(\vec{r}_{GDZsph3D} \right)}[radians] = \lambda{\left(\vec{r}_{GDZsph3D} \right)}\end{equation} \begin{equation}\operatorname{SLT}{\left(\vec{r}_{GDZsph3D} \right)}[hr] = \lambda{\left(\vec{r}_{GDZsph3D} \right)}\end{equation} \begin{equation}\operatorname{TEC}{\left(\vec{r}_{GDZsph3D} \right)}[\frac{10000000000000000}{m^{2}}] = \lambda{\left(\vec{r}_{GDZsph3D} \right)}\end{equation} \begin{equation}\rho_{N2}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{N2+}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{NO}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{NO+}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O2}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O2+}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O3P}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{O+4S4P}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\rho_{n}{\left(\vec{r}_{GDZsph4D} \right)}[\frac{kg}{m^{3}}] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{T_{n}}{\left(\vec{r}_{GDZsph4D} \right)}[K] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{ieast}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{inorth}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{iup}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{neast}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{nnorth}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{v_{nup}}{\left(\vec{r}_{GDZsph4D} \right)}[m / s] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation}
Functionalization method 2¶
Load a single or multiple variables with the gridded versions.
Note:
- Requesting variables that are NOT in the list above triggers a printed message: '... name not recognized'.
- Requesting variables that ARE in the list above but not in the file triggers a printed message: '...not available'.
In [5]:
Copied!
# This is the most common method to functionalize the desired data.
kamodo_object_2 = reader(file_dir, variables_requested=['T_n', 'T_i'])
kamodo_object_2
# This is the most common method to functionalize the desired data.
kamodo_object_2 = reader(file_dir, variables_requested=['T_n', 'T_i'])
kamodo_object_2
Some requested variables are not available in the files found: dict_keys(['2DANC', '3DLST']) ['T_i']
Out[5]:
\begin{equation}\operatorname{T_{n}}{\left(\vec{r}_{GDZsph4D} \right)}[K] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation} \begin{equation}\operatorname{T_{n ijk}}(time[hr],lon[deg],lat[deg],height[km])[K] = \lambda{\left(time,lon,lat,height \right)}\end{equation}
Functionalization method 3¶
Load a single or multiple variables without the gridded version(s).
In [6]:
Copied!
# This is what is used in Kamodo's flythrough.
kamodo_object_3 = reader(file_dir, variables_requested=['T_n', 'T_i'], gridded_int=False)
kamodo_object_3
# This is what is used in Kamodo's flythrough.
kamodo_object_3 = reader(file_dir, variables_requested=['T_n', 'T_i'], gridded_int=False)
kamodo_object_3
Some requested variables are not available in the files found: dict_keys(['2DANC', '3DLST']) ['T_i']
Out[6]:
\begin{equation}\operatorname{T_{n}}{\left(\vec{r}_{GDZsph4D} \right)}[K] = \lambda{\left(\vec{r}_{GDZsph4D} \right)}\end{equation}
Interacting with a kamodo object¶
In [7]:
Copied!
# Show the datetime object for midnight of the first day of the dataset.
kamodo_object_default.filedate
# Show the datetime object for midnight of the first day of the dataset.
kamodo_object_default.filedate
Out[7]:
datetime.datetime(2015, 3, 17, 0, 0, tzinfo=datetime.timezone.utc)
In [8]:
Copied!
# Print the maxima, minima, and units of each coordinate grid.
MW.Coord_Range(kamodo_object_default, ['T_n', 'T_n_ijk'])
# Print the maxima, minima, and units of each coordinate grid.
MW.Coord_Range(kamodo_object_default, ['T_n', 'T_n_ijk'])
The minimum and maximum values for each variable and coordinate are: T_n: time: [0.0, 23.83333396911621, 'hr'] lon: [-180.0, 180.0, 'deg'] lat: [-90.0, 90.0, 'deg'] height: [96.62001037597656, 640.3912963867188, 'km'] T_n_ijk: time: [0.0, 23.833334, 'hr'] lon: [-180.0, 180.0, 'deg'] lat: [-90.0, 90.0, 'deg'] height: [96.62001, 640.3913, 'km']
In [9]:
Copied!
# Example of interpolation command for two points for a regular function.
# This is the method used in CCMC Kamodo's flythrough.
kamodo_object_default['T_n']([[22.5, -20.5, -20.5, 350.], [22.7, -20.5, -20.5, 350.]])
# Example of interpolation command for two points for a regular function.
# This is the method used in CCMC Kamodo's flythrough.
kamodo_object_default['T_n']([[22.5, -20.5, -20.5, 350.], [22.7, -20.5, -20.5, 350.]])
Time slice index 135 added from file. Time slice index 136 added from file. Time slice index 137 added from file. Time slice index 138 added from file.
Out[9]:
array([1184.29853082, 1184.16026839])
In [10]:
Copied!
# Example of interpolation command for a gridded function.
# The value will be the same two values as the previous block's result.
# The gridded functions slice through the data at the values given.
kamodo_object_default['T_n_ijk'](time=[22.5, 22.7], lon=-20.5, lat=-20.5, height=350.)
# Example of interpolation command for a gridded function.
# The value will be the same two values as the previous block's result.
# The gridded functions slice through the data at the values given.
kamodo_object_default['T_n_ijk'](time=[22.5, 22.7], lon=-20.5, lat=-20.5, height=350.)
Out[10]:
array([1184.29853082, 1184.16026839])
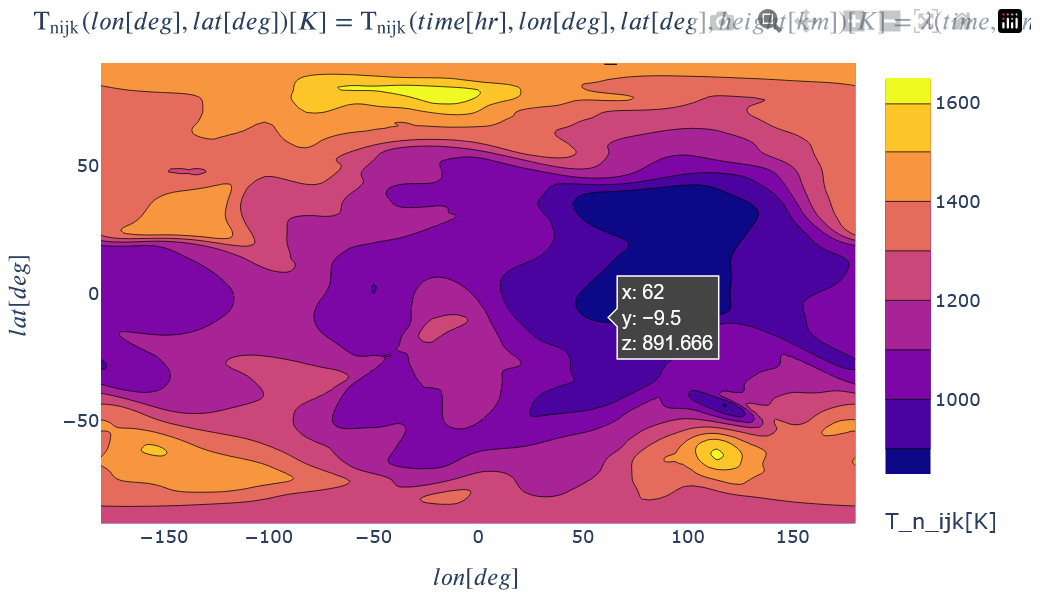
An example of Kamodo's default 2D plot.
kamodo_object_default.plot('T_n_ijk', plot_partial={'T_n_ijk': {'time': 22.5, 'height': 350.}})