Constellation Mission Planning Tool¶
This notebook tutorial shows how to fly a constellation of satellites through model data, focusing on spherical coordinate examples as an introduction. Trajectories can be obtained either from the test GDC trajectory file or the flythrough trajectory functions as shown here. See the Satellite Trajectory section for examples on trajectory options, and the Choosing Models and Variables section for more information on choosing models and variables. This functionality is not available from the command line. More complex workflow examples are included in the notebooks directory on the main level.
Preparing to run¶
# For a given model, find out what time range is covered by the data in a given directory.
from kamodo_ccmc.flythrough import model_wrapper as MW
import datetime as dt
model, file_dir = 'GITM', 'D:/GITM/jasoon_shim_071418_IT_1_tenth_oneday/' # change to match your machine
start_utcts = dt.datetime(2015, 3, 17, 0).replace(tzinfo=dt.timezone.utc).timestamp()
end_utcts = dt.datetime(2015, 3, 17, 6).replace(tzinfo=dt.timezone.utc).timestamp()-1
# This function also automatically performs any data preparation needed.
# Import function to retrieve the grace1 trajectory from the SSCWeb.
from kamodo_ccmc.flythrough import SatelliteFlythrough as SF
# Typical coordinates possible through SSCWeb are GEO, GSE, SM, and GSM (all cartesian and in R_E).
input_coord = 'GEO'
traj_dict, coord_type = SF.SatelliteTrajectory('grace1', start_utcts, end_utcts, coord_type=input_coord)
C:\Users\rringuet\Anaconda3\envs\Kamodo_Jan2023\lib\site-packages\spacepy\time.py:2367: UserWarning: Leapseconds may be out of date. Use spacepy.toolbox.update(leapsecs=True)
warnings.warn('Leapseconds may be out of date.'
Attribute/Key names of return dictionary: dict_keys(['sat_time', 'c1', 'c2', 'c3'])
# Convert coordinates to system desired for reconstruction to take place in.
# The trajectories were retrieved in GEO cartesian, and are converted to GEO spherical below.
from kamodo_ccmc.flythrough.utils import ConvertCoord
c1, c2, c3, units = ConvertCoord(traj_dict['sat_time'], traj_dict['c1'], traj_dict['c2'], traj_dict['c3'],
input_coord, 'car', input_coord, 'sph')
print(c1.min(), c1.max(), c2.min(), c2.max(), c3.min(), c3.max())
-177.97713698151003 170.68868826059744 -88.76818132167068 88.97299240106359 1.0600288778760936 1.0644534136698656
# Choose a variable from the model data chosen.
MW.Variable_Search('', model, file_dir)
The file directory contains the following standardized variable names: ----------------------------------------------------------------------------------- rho_N2 : '['mass density of molecular nitrogen', 13, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_N2plus : '['mass density of molecular nitrogen ion', 14, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_NO : '['mass density of nitric oxide', 20, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_NOplus : '['mass density of nitric oxide ion', 21, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_O2 : '['mass density of molecular oxygen', 22, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_O2plus : '['mass density of molecular oxygen ion', 24, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_O3P : '['mass density of atomic oxygen (3P state)', 27, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_Oplus4S4P : '['mass density of atomic oxygen ion (4S or 4P state)', 28, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' rho_n : '['neutral mass density', 30, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'kg/m**3']' T_n : '['neutral temperature', 31, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'K']' v_ieast : '['zonal ion wind velocity (east)', 32, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'm/s']' v_inorth : '['meridional ion wind velocity (north)', 33, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'm/s']' v_iup : '['vertical ion wind velocity (up)', 34, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'm/s']' v_neast : '['zonal neutral wind velocity (east)', 35, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'm/s']' v_nnorth : '['meridional neutral wind velocity (north)', 36, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'm/s']' v_nup : '['vertical neutral wind velocity (up)', 37, 'GDZ', 'sph', ['time', 'lon', 'lat', 'height'], 'm/s']' SZA : '['solar zenith angle', 48, 'GDZ', 'sph', ['time', 'lon', 'lat'], 'radians']' SLT : '['solar local time', 63, 'GDZ', 'sph', ['time', 'lon', 'lat'], 'hr']' TEC : '['vertical total electron content (height integrated from bottom to top boundary)', 91, 'GDZ', 'sph', ['time', 'lon', 'lat'], '10**16/m**2']'
# Bring up documentation for the reconstruction functionality.
from kamodo_ccmc.flythrough.Reconstruction_v0 import RECON
RECON.__doc__.split('\n')
['Uses shifted copies of the satellite trajectory to reconstruct ', ' the model data for the variable name given.', ' ', " - model: 'CTIPe', 'IRI', 'GITM', 'SWMF_IE', 'TIEGCM'", ' - variable_name = choose from list of standardized variable names from model chosen', ' - file_dir = file path to model data', ' - sat_time: a numpy array of the utc timestamps', ' - c1, c2, c3: numpy arrays of the positions correlating to the utc timestamps', ' (c1, c2, c3) should be (x,y,z) in R_E for cartesian coordinates, and (lon, lat, ', ' radius (R_E) or altitude (km)) for spherical coordinates. ', " - coord_type: one of 'GDZ', 'GEO', 'GSM', 'GSE', 'SM', 'GEI', 'MAG', 'SPH', 'RLL'", " - coord_grid: either 'car' or 'sph'. Note that not all combinations ", " make sense (e.g. 'SPH' and 'car') and are not allowed. ", ' Note that GDZ sph is the only coordinate system that assumes the third coordinate', ' is an altitude and is in km. All other spherical coordinate systems expect', ' a radius in R_E, and all cartesian coordinate systems expect x, y, z values', ' in R_E. All times should be in UTC timestamps.', ' - recon_option = string representing reconstruction and comparison method', " Choose from 'UnMod_AvgSlice','UnMod_AvgDSlice','AvgMod_AvgSlice',", " 'AvgMod_AvgDSlice', 'UnMod_OrbitSliceD', 'UnMod_OrbitSliceN', 'AvgMod_OrbitSliceD',", " and 'AvgMod_OrbitSliceN'", ' - UnMod means the satellite trajectory is not modified', ' - AvgMod means the dimensions not reconstructed are replaced with either ', ' the average value of the original and offset satellite trajectories or', ' the value given in the xx_avg keywords.', ' - AvgSlice means recon is compared with a slice at the average dimensions ', ' not reconstructed, again using either the average or the given value ', ' in the xx_avg keywords.', ' - AvgDSlice means recon is compared with an average of all the slices ', ' in the range of the dimensions not reconstructed. Weighted averages', ' are not supported.', ' - OrbitSlice means the model data is retrieved along all trajectories ', ' in the given constellation instead of along a given dimensional average.', ' The OrbitSlice option is what an inifite number of satellites would', ' see if positioned along the trajectory with time offsets t+dt, where', ' dt is the difference in time between satellites along the orbit. For ', ' computation purposes, the user may enter the value of dt in seconds ', ' in the input line or use the default of 60 seconds. The trajectories', ' are split into orbits, defined as where the latitude differential ', ' changes from positive to negative, and then extracted from the model', " for the calculated time grid. The 'D' and 'N' variations are for", ' retrieving only the day or night portions of the orbit rather than ', ' the entire orbit to avoid averaging data of different natures. Whether', ' a given time+spatial coordinate is on the day or night side is ', ' determined by converting the time+spatial coordinates of the orbit slices', ' into GSE spherical coordinates and filtering based on longitude.', ' The longitude logic compensates to keep equatorial crossing in GSE', ' at the same MLT as the original set.', ' NOTE: Orbital slicing may not produce the desired result in cartesian ', ' coordinates.', ' - recon_dims = string representing choice of dimensions to use in reconstruction', " 'tc1','tc2','tc3','c1c2','c1c3','c2c3' are the options. ", ' The first name is the x-axis, and the second name is the y-axis.', ' - time_offsets: a list of time offsets in seconds to be applied to the trajectories (in s)', ' - c1_offsets: a list of offsets to be applied to the c1 coordinate in the trajectory', ' in the same units indicated by the coordinate system options', ' - c2_offsets: a list of offsets to be applied to the c2 coordinate in the trajectory', ' in the same units indicated by the coordinate system options', ' - c3_offsets: a list of offsets to be applied to the c3 coordinate in the trajectory', ' in the same units indicated by the coordinate system options', ' - the offset lists entered MUST BE THE SAME LENGTH or be equal to [0.], and', ' must be in the same coordinate system and units as the input coordinates.', ' - t_avg: the average time in UTC seconds used for when time is not a reconstructed', ' dimension and the recon_option chosen requires averaging. Default is', ' the average time of the entire set of input and offset trajectories.', ' - c1_avg: the average c1 value used for when c1 is not a reconstructed', ' dimension and the recon_option chosen requires averaging. Default is', ' the average c1 value of the entire set of input and offset trajectories.', ' - c2_avg: the average c2 value used for when c2 is not a reconstructed', ' dimension and the recon_option chosen requires averaging. Default is', ' the average c2 value of the entire set of input and offset trajectories.', ' - c3_avg: the average c3 value used for when c3 is not a reconstructed', ' dimension and the recon_option chosen requires averaging. Default is', ' the average c3 value of the entire set of input and offset trajectories. ', ' - dx = grid resolution for the x axis in the same units as x, default of 2. ', ' - dy = grid resolution for the y axis in the same units as y, default of 2.', ' - d1 = grid resolution for the first non-reconstructed dimension. Only used', ' if _AvgDSlice options are chosen and if slicing in local time. Default=0.', ' - d2 = grid resolution for the second non-reconstructed dimension. Only used', ' if _AvgDSlice options are chosen. Default=0.', ' - dt = time resolution of sampling for orbit slicing option. Default=60 s.', " - run_option = one of 'all' or 'flythrough'. Default is all.", ' Note: The dx and dy values are assumed to be in the units of the associated ', ' coordinate indicated by the coordinate options (s, R_E, deg, or km).', ' Note: When reconstructing in two spatial cartesian coordinates ', ' (e.g. xy, yz, or xz), filter the input satellite trajectory to only ', ' include times where the third spatial dimension inputs are either ', ' positive OR negative values to avoid a combined reconstruction of both ', ' hemispheres in the same plots. For example, if you wish to perform a', ' reconstruction of the x and y dimensions in spatial coordinates for', ' the North Pole, then filter the satellite trajectory to only include', ' times where the z dimension is positive. Similarly, reconstructions of', ' the South Pole can be performed by simply filtering out the times where', ' the z dimension is positive. This filtering is not needed when time is', ' one of the reconstructed dimensions, but it can be done if desired.', ' Example: ', ' import numpy as np', " pos_idx = np.where(results['c3']>0.)[0] #North Pole is z>0.", " time = results['utc_time'][pos_idx]", " c1 = results['c1'][pos_idx]", " c2 = results['c2'][pos_idx]", " c3 = results['c3'][pos_idx]", ' Cartesian note: For cartesian reconstructions of nearly spherical ', " trajectories, 'Unmod_AvgDSlice' option is recommended to avoid reconstructing", ' a ring of data around the Earth. Reconstructions will be better achieved', ' in spherical coordinates for these scenarios. To easily switch between', ' coordinate systems, from GSE cartesian to GEO spherical, for example:', ' from kamodo_ccmc.flythrough.utils import ConvertCoord', ' lon, lat, radius, units = ConvertCoord(utc_time,x,y,z,', " 'GSE','car','GEO','sph')", ' See the relevant flythrough example notebook for more details on this function.', ' ']
# Choose inputs.
variable_name = 'rho_n' # from chosen files above
recon_dimensions = 'c1c2' # Longitude vs Latitude reconstruction for spherical coordinates
recon_option = 'UnMod_AvgDSlice'
# fly the given trajectory through the data unmodified, then fly the reconstructed coordinate grid through the data
# after taking the average of t and height.
# Set up constellation input:
lon_offsets = [0., 30., 60., 90., 120., 150.] # 6 satellites equally spaced in longitude
# Choose the grid resolution of reconstruction. The finer the resolution, the longer the program takes to run and
# the more 'holes' you will see in the reconstructed plot. Physically, these should be set to the instrument's
# field of view in the units of the input coordinate system (e.g. degrees for longitude and latitude, seconds for
# time, etc).
dx, dy = 5., 5. # Since recon_dimensions='c1c2', dx is resolution in longitude, and dy is the resolution in latitude.
d1, d2 = 1800., 0.001 # time (in s) and height (in R_E) resolution of sampling for averaging
Execution¶
# Run the reconstruction.
# This process typically takes up to a few minutes, but can take up to ~2 hours or more depending on the amount of data
# used, the grid resolution chosen, the reconstruction method chosen, and whether conversion to pressure level is
# required. As originally set, the process takes about 360 seconds.
# Make sure to include all desired offsets in this block before executing.
recon = RECON(model, variable_name, file_dir, traj_dict['sat_time'], c1, c2, c3,
input_coord, 'sph', recon_option, recon_dimensions, c1_offsets=lon_offsets, dx=dx, dy=dy, d1=d1, d2=d2)
Performing satellite constellation flythrough for 2160 locations... Time slice index 0 added from file. Time slice index 1 added from file. Time slice index 2 added from file. Time slice index 3 added from file. Time slice index 4 added from file. Time slice index 5 added from file. Time slice index 6 added from file. Time slice index 7 added from file. Time slice index 8 added from file. Time slice index 9 added from file. Time slice index 10 added from file. Time slice index 11 added from file. Time slice index 12 added from file. Time slice index 13 added from file. Time slice index 14 added from file. Time slice index 15 added from file. Time slice index 16 added from file. Time slice index 17 added from file. Time slice index 18 added from file.
C:\Users\rringuet\Anaconda3\envs\Kamodo_Jan2023\lib\site-packages\scipy\interpolate\interpolate.py:630: RuntimeWarning: divide by zero encountered in true_divide slope = (y_hi - y_lo) / (x_hi - x_lo)[:, None] C:\Users\rringuet\Anaconda3\envs\Kamodo_Jan2023\lib\site-packages\scipy\interpolate\interpolate.py:633: RuntimeWarning: invalid value encountered in multiply y_new = slope*(x_new - x_lo)[:, None] + y_lo
Time slice index 19 added from file. Time slice index 20 added from file. Time slice index 21 added from file. Time slice index 22 added from file. Time slice index 23 added from file. Time slice index 24 added from file. Time slice index 25 added from file. Time slice index 26 added from file. Time slice index 27 added from file. Time slice index 28 added from file. Time slice index 29 added from file. Time slice index 30 added from file. Time slice index 31 added from file. Time slice index 32 added from file. Time slice index 33 added from file. Time slice index 34 added from file. Time slice index 35 added from file. Time slice index 36 added from file. Time slice index 37 added from file. Gridding data for LonLat...done in 0.11941s for 2701 gridpoints. Performing non-averaged grid flythrough for 162060 locations. Converting 162060 positions into GDZsph coordinates...done in 18.9057 seconds. Time slice index 0 added from file. Time slice index 1 added from file. Time slice index 2 added from file. Time slice index 4 added from file. Time slice index 5 added from file. Time slice index 7 added from file. Time slice index 8 added from file. Time slice index 10 added from file. Time slice index 11 added from file. Time slice index 14 added from file. Time slice index 15 added from file. Time slice index 17 added from file. Time slice index 18 added from file. Time slice index 20 added from file. Time slice index 21 added from file. Time slice index 23 added from file. Time slice index 24 added from file. Time slice index 27 added from file. Time slice index 28 added from file. Time slice index 30 added from file. Time slice index 31 added from file. Time slice index 33 added from file. Time slice index 34 added from file. Time slice index 36 added from file. Time slice index 37 added from file. Grid flythrough completed in 36.82967 s. Reconstruction program complete in 39.31747 s.
# The output of the function is a Kamodo object with all of the default features described in documentation.
# rho_n is the reconstructed data from the constellation flythrough. rho_n_model is the data from the model in the
# method chosen. PercentDiff is the percent difference between the two, calculated using
# PercentDiff = (rho_n_model - rho_n)/rho_n_model*100.
recon
Comparing the results¶
Nicer version of default Kamodo plot
from kamodo_ccmc.tools.plotfunctions import toColor
toColor(recon.plot(rho_n=dict(Lon=recon.x, Lat=recon.y)), colorscale='Viridis')
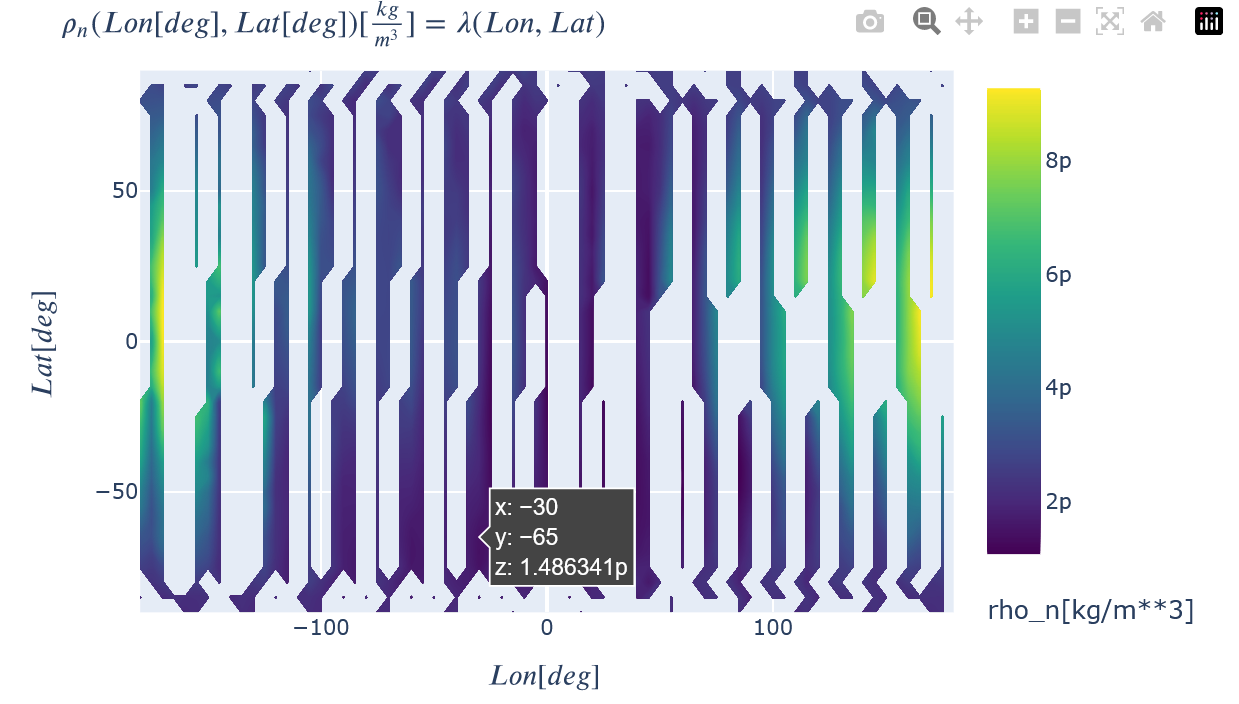
toColor(recon.plot(rho_n_model=dict(Lon=recon.x, Lat=recon.y)), colorscale="Viridis")
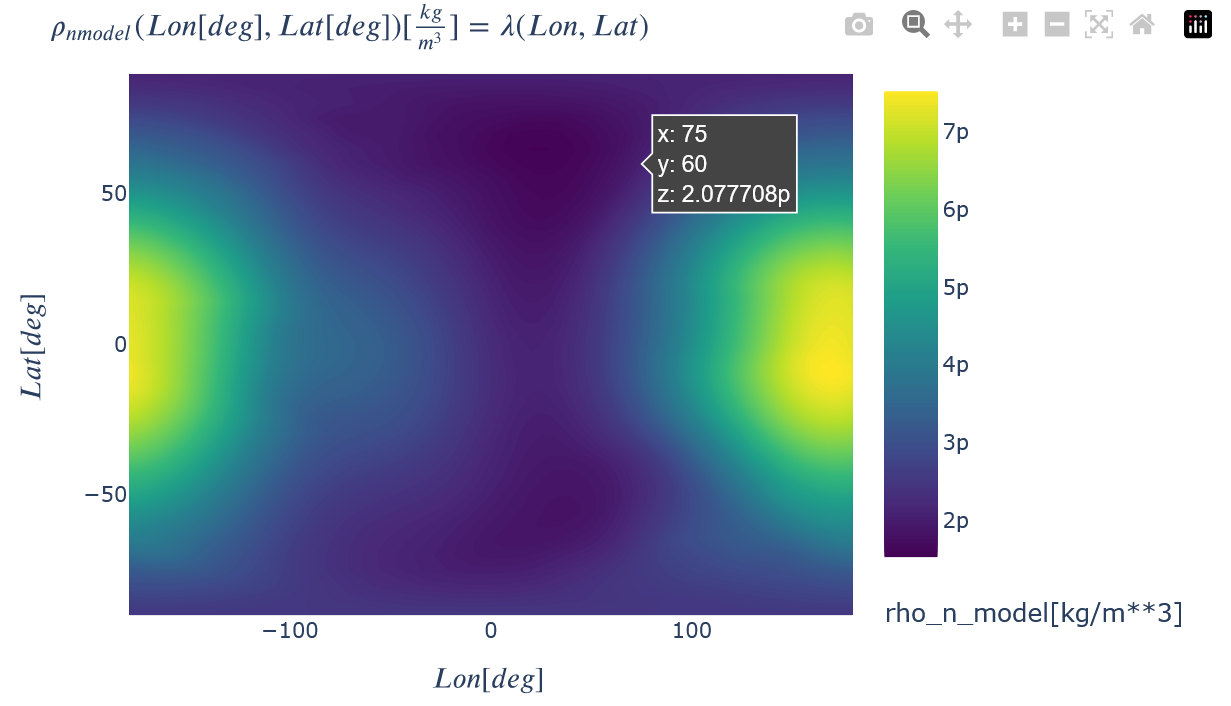
Show the percent difference between the two. A percent difference of zero is an exact match. How well the reconstructed plot matches the model plot not only depends on the constellation arrangement, but also on the reconstruction method chosen. The 'AvgMod_...' options typically result in the better matches, but are not physically representative of what the constellation will 'see' in real data because the two non-reconstructed dimensions are ignored in the input satellite trajectory (e.g. an average value for both height and time are used instead of the full range for a Lon-Lat reconstruction). The unmodified options ('Unmod_...') are thus recommended as the more physical comparison because the full set of input trajectory values are used.
toColor(recon.plot(PercentDiff=dict(Lon=recon.x, Lat=recon.y)), colorscale="Viridis")
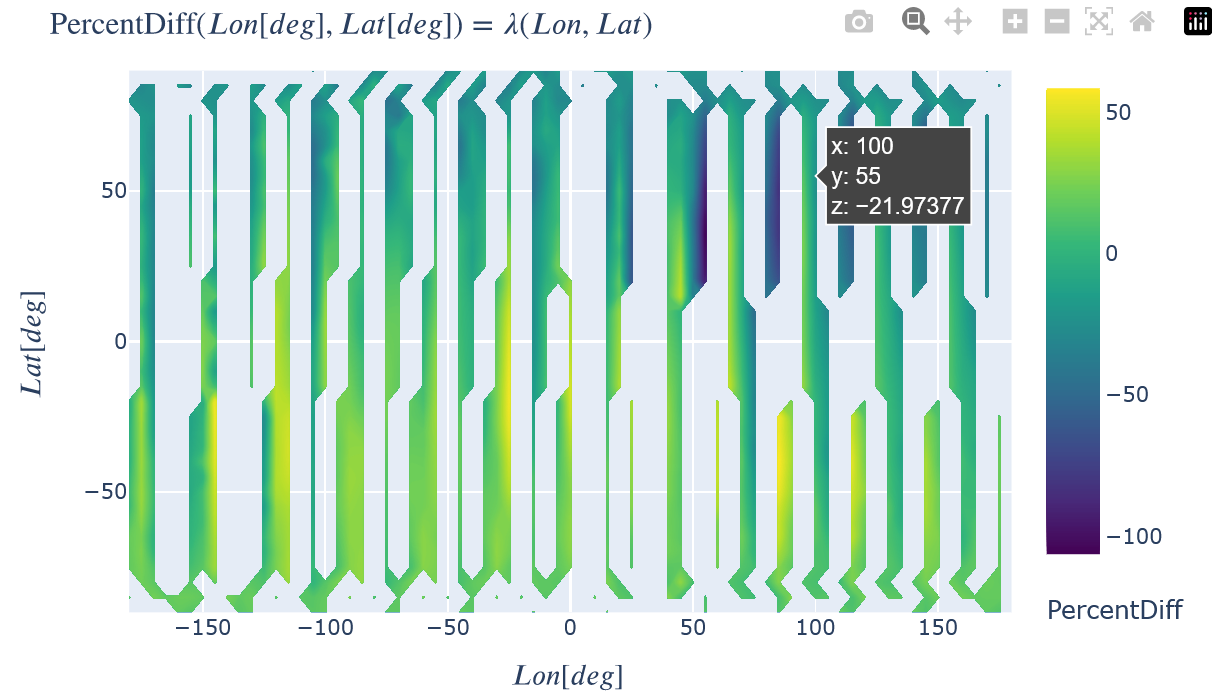
# Retrieve the percent difference data values and show in a histogram, ignoring NaN values.
# Some extra logic is required to automatically enforce bins of width 2%
import numpy as np
import matplotlib.pyplot as plt
pdiff_data = recon.PercentDiff()
data_min, data_max = np.floor(np.nanmin(pdiff_data)), np.ceil(np.nanmax(pdiff_data))
num_bins = int((data_max-data_min)/2.)
if num_bins<5:
num_bins=20
hist, edges, patches = plt.hist(np.ravel(pdiff_data), range=(data_min,data_max),bins=num_bins)
plt.xlabel('Percent Difference')
plt.ylabel('Frequency')
Text(0, 0.5, 'Frequency')