Software Design

The following sections describe the overall software design and architecture, including design rationale. We especially highlight impacts on computational performance and complexity.

Software Architecture

The primary function of the unsteady Pressure-Sensitive Paint (uPSP) software is to process raw wind tunnel test data to produce time histories of flowfield pressure measurements on the surface of a wind tunnel model. This function is implemented using a set of software applications that can be run from a UNIX command-line interface (CLI):

1. upsp-extract-frames: Dumps individual frames from, or transcode video format of, high-speed camera video files.

2. upsp-external-calibration: Computes external camera calibration relative to the model position and orientation as viewed in a single camera frame. The first frame from each video file (dumped using upsp-extract-frames) is used to calibrate each camera’s positioning relative to the model at the start time of the test condition

3. psp_process: Projects image pixel values from each video frame onto a 3D grid representation of the wind tunnel test model surface, and convert into surface pressure values

The computationally-intensive processing is primarily within psp_process, which is a monolithic, highly-parallelized C++ application (psp_process).

In addition to the primary processing applications, a Python-based preprocessing application, upsp-make-processing-tree, is provided to allow users to configure inputs to psp_process for batch processing in the NAS environment.

Pipeline Application Design Details

The following section describes each pipeline application in more detail, including:

• Functional flow: Flow of data into, throughout, and out of the application

• Algorithms: Algorithms used by the application

• Implementation details: Details related to requirements imposed on target compute systems — memory management, disk usage, parallelization considerations

• Design rationale: Context for architectural/design decisions related to the application

upsp-extract-frames

The upsp-extract-frames application helps extract individual frames from supported high-speed camera video files and save them in more portable image file format(s). It can also encode segments of the video file into more portable video format(s). It makes use of the OpenCV VideoWriter and imsave API elements, meaning it can encode images and video in formats supported by the OpenCV installation.

The application’s primary use in the processing pipeline is to extract the first frame from the video file, which is then used by upsp-external-calibration.

upsp-external-calibration

The external calibration pipeline implements a coarse and refined stage to iteratively improve the calibration quality. For both stages, the goal is to match 3D target positions with image locations and optimize the extrinsic parameters such that the re-projection error is minimized. The coarse stage takes an initial guess for the position and orientation (pose) based on the wind-off model position and updates the guess. The refined stage uses the coarse solution and further refines it. Typically, the initial guess has a re-projection error > 5 pixels, the coarse solution has an error of ~1 pixels, and the refined solution is < 1 pixel.

Coarse Stage

The coarse stage begins with the inputs described in the uPSP User Manual. The process is outlined in Fig. 3. The first steps of the coarse stage are to get the wind-off visible targets, and detect image targets. Targets must be detected since the re-projection error from the wind-off external calibration guess is typically high, and the expected image positions can be far enough that the expected location is not within the associated target. This can cause ambiguity with matching, or errors in matching to image noise.

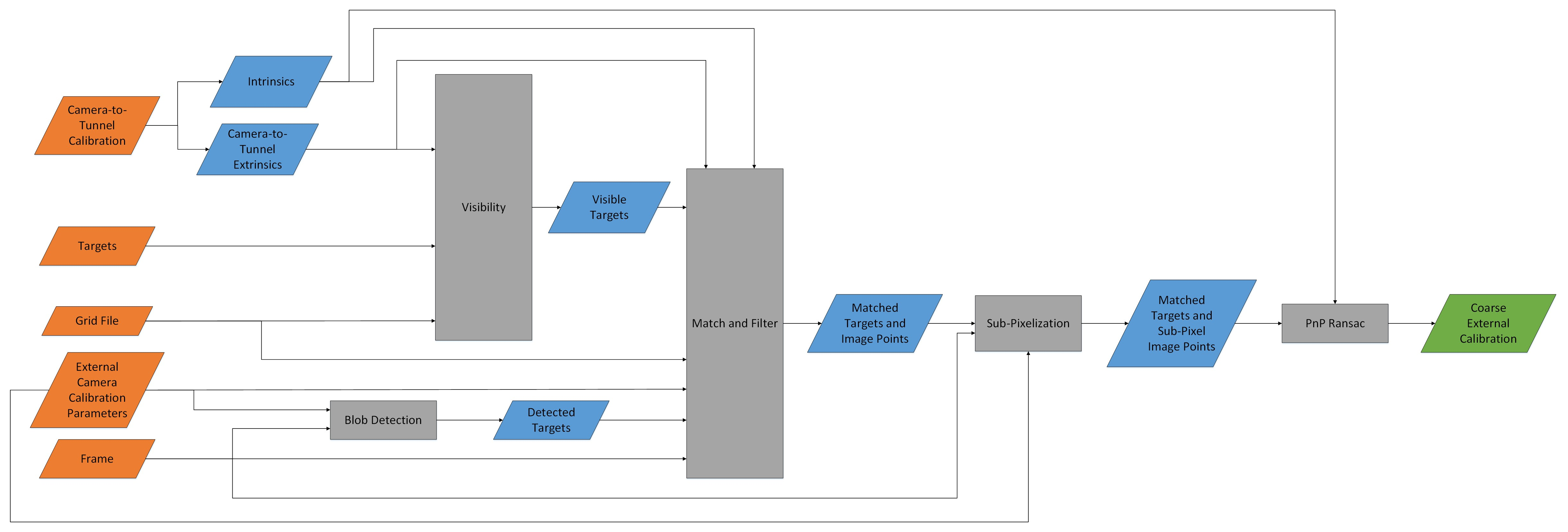
Fig. 3 External Calibrate (Coarse) Functional Flowchart.

To get the wind-off visible targets, the wind-off camera-to-model extrinsics must be found. The wind-off camera-to-model extrinsics are obtained by generating a model-to-tunnel transform, and combing it with the camera-to-tunnel transform found in the camera-to-tunnel calibration file. The model-to-tunnel transform is generated from the WTD file and tunnel/model properties in the external camera calibration parameters. With the wind-off extrinsics known, the Bounding Volume Hierarchy (BVH) visibility checker module is used to find the wind-off visible targets. See BVH Visibility Checker for details on how the visibility check is performed.

The detected image targets are found using OpenCV’s blob detection. The parameters for blob detection are saved in the external camera calibration parameters. The image is first pre-processed by scaling the image intensity between 0 and the largest inlier pixel intensity. Details on the pre-processing algorithm are available in Image Pre-Processing.

The wind-off visible targets, and the detected image targets can then be matched and filtered. Details on the matching and filtering process are available in Matching and Filtering.

Once matched and filtered, the remaining matches have the detected image target sub-pixel localized. Details on the sub-pixel localization algorithm are available in Sub-Pixel Localization. The resulting targets and sub-pixel image locations are processed with OpenCV’s PnPRansac to determine the extrinsic parameters that minimize the re-projection error. These first stage extrinsic parameters are known as the coarse external calibration.

Refined Stage

The refined stage begins with the same inputs, but the added benefit of having the coarse external calibration. The process is outlined in Fig. 4. The refined stage has the same general steps as the coarse stage: get the visible targets and image locations, match and filter them, sub-pixel localize, and PnPRansac. However, instead of using blob detection, projection is used for the image locations. Projection is used here since the re-projection error from the coarse external calibration is typically small, and the projected locations almost always lie within the associated target.

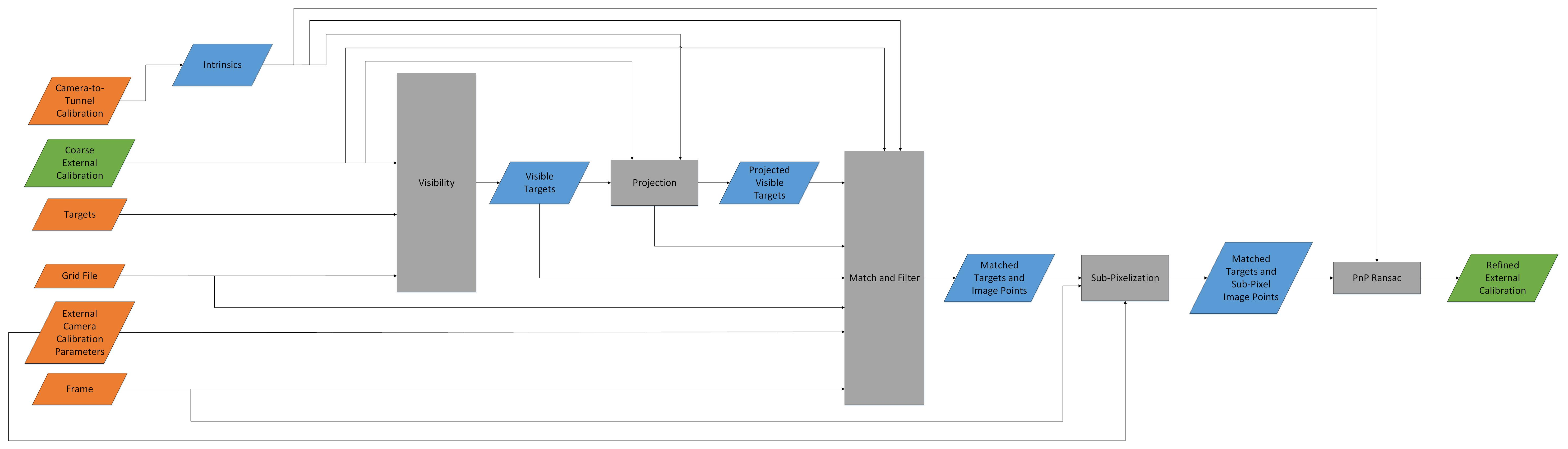
Fig. 4 External Calibrate (Refined) Functional Flowchart.

The first steps of the refined stage are to find the visible targets, and the projected locations of those visible targets based on the coarse external calibration. The same BVH as used in the coarse stage is used in the refined stage. The matching stage is trivial since the projected locations are generated 1:1 from the visible targets. Projection is done using OpenCV’s projectPoints.

With the visible targets and their projected locations, the same filtering process used in the coarse stage is used here. The image locations are then sub-pixel localized, and OpenCV’s PnPRansac is used on the visible targets and sub-pixel localized image locations. The second stage external calibration parameters are known as the refined external calibration, and are written to the external calibration output file to be used in psp_process.

Algorithms

The algorithms used in the external calibration are the image pre-processing, BVH visibility checker, matching and filtering, and sub-pixel localization.

Image Pre-Processing

The image pre-processing is used in an attempt to normalize the pixel intensity of the model across all data points. Due to variations in wind speed, and degradation of the paint due to UV exposure, the model can be significantly brighter or darker day to day or tunnel condition to tunnel condition. To normalize this, the image intensity is scaled from 0 to the largest inlier pixel intensity. This is done by converting the image to a floating point numpy.ndarray (rather than a uint8 or uint16), dividing by the largest inlier pixel intensity, clipping the maximum value to 1, then multiplying by 255 (or 4095 if using 16-bit).

The largest inlier pixel intensity is defined as the largest value in the sorted list of pixel intensities where a substantially far pixel must is at least 90% the intensity as the current pixel. Substantially far is defined as 0.001 * the current pixel’s index.

It is easier to see in the code:

i = len(img_flat_sorted) - 1
while (0.9 * img_flat_sorted[i] > img_flat_sorted[int(np.rint(i * 0.999))]):
   i -= 1
max_val = img_flat_sorted[i]

So in a 1024 x 512 image with 524,288 pixels, in order for the brightest pixel to be considered an inlier (position 524,287 in the sorted list), the value at position 523,763 must be at least 90% of its intensity. If it is not, the second brightest pixel is checked, and this continues down until an inlier is found.

This intensity check relative to other pixel intensities ensures that a small number of very bright pixels do not cause the scaling of the image to be controlled by that small group. Should a small number of pixels be very high due to saturation from glare, or hot pixels due to sensor error, those will be deemed outliers and have their intensity clipped to 256 (or 4095).

BVH Visibility Checker

The Bounding Volume Hierarchy (BVH) checks the visibility of a point with known position and normal vector. This can be a grid node, target, or other point of interest so long as it has a position and normal vector.

To determine if a point is visible, the BVH visibility checker first checks if that point has an oblique viewing angle greater than that specified in the external calibration parameters. Typically, a value of 70° is used for the maximum allowable oblique viewing angle since points with oblique viewing angles greater than that become difficult to view due to perspective distortion. Points that pass the check are then passed to the BVH to check for occlusions.

The oblique viewing angle is defined as the angle between the point’s normal vector, and the vector from the point to the camera. If the point fails that check, it is immediately deemed not visible. In reality, it may be visible if the oblique viewing angle is between 70°, and 90°. However, above 70° and the point experiences significant perspective distortion. For grid nodes, this means poor pixel intensity association and thus a pressure with large uncertainty. For targets, this means a large sub-pixel localization error. This operation is similar to back-face culling, and would be identical the back-face culling if the oblique viewing angle was set to 90°. Just as with back-face culling, the oblique viewing angle check is significantly less expensive than the occlusion checks. Therefore, oblique viewing angle is checked first since any points removed will not have to undergo the expensive occlusion checks. With 70°, on average about 60% of the points will be rejected.

Points that pass the oblique viewing angle check are passed to the bounding volume hierarchy to check for occlusions. The BVH is a recursive data structure that can efficiently check for the intersection between a mesh and a ray (O(logn) where n is the number of mesh nodes). The mesh in this case is the model grid, and the ray is the ray between the point and the camera. The ray origin is actually taken to be the point location, plus a small distance (1e-4”) along the point’s normal vector rather than the point’s location directly. This ensures that if the point is exactly on the model surface (or even inside the model by a small amount), it is not wrongfully deemed occluded.

Points that pass both the oblique viewing angle check and the occlusion check are deemd visible. Note, for target the point is typically taken to be the center location. This assumes that the if the center of the target is visible, then all of the target is visible. For mesh nodes, usually all vertices of the node are checked. If all are visible, it is assumed that the entire 2D surface of the node is visible. These are reasonable assumptions since the targets, and especially the mesh nodes, are relatively small. So if the center is visible it is very likely that the entire target/node is visible.

Matching and Filtering

The matching process matches 3D targets to detected image locations. To do this, the 3D targets are projected into the image. Each projected location is then matched to the nearest detected image target. Once all visible targets are matched, any matches that are not one-to-one (detected image targets matched to multiple projected locations) are thrown out. Additionally, matches are thrown out if the pixel distance between the projected location and detection image target location is over the max_dist threshold (specified in the external camera calibration parmeters). Matches are further filtered if any 2 image locations are closer than the min_dist threshold (specified in the external camera calibration parmeters).

Sub-Pixel Localization

The sub-pixel localization fits a 2D Super-Gaussian distribution to a cropped region around an image target. The idea being to improve a rough localization found with blob detection or 3D projection. A 2D Super-Gaussian approximate the form of an image target, and therefore the 2D mean location can be taken to be the target’s center location. For (ideal) sharpie targets with diameter ~4-5 pixels, the median error is ~0.05 pixels, and is within 0.265 pixels 99.9% of the time.

The algorithm is performed by defining a 2D Super Gaussian function, then optimizing the gaussian function parameters to the cropped image region using Scipy’s curvefit module.

Design Rationale

Ideally, the external calibration routine would begin with a very close initial guess. Close here can refer to a max re-projection error of ~1 pixel. With a low re-projection error, the targets could be projected into the image, then the region around the projected location could be passed through the sub-pixel localization algorithm. The targets and sub-pixel localized image locations could then be passes to OpenCV’s PnPRansac. This would be akin to performing just the refined external calibration stage from the initial guess. However, using the wind-off pose yields a max re-projection error > 3 pixels and > 5 pixels in some cases.

The radius of the sharpie targets is ~2.5 pixels, so in many cases the projected locations are not even inside the sharpie target. In order for the cropped region of the image passed to the sub-pixel localization to contain the entire target, the radius of the cropped region would have to be ~9 pixels (5 pixels to contain the center of the sharpie target plus 2.5 pixels to contain the whole target, plus 1.5 pixels to have a pixel between the edge and the target). A region that large is likely to pick up noise, image background, or other features that would cause the sub-pixel localization routine to produce bad results. Therefore, a two- stage, iterative method is used instead.

The first stage (coarse optimization) uses blob detection to find the target image locations rather than projection. The projected locations will still be close to the detected locations to likely be correct and unambiguous. The goal of the first stage is to set up the ‘ideal’ initial guess previously mentioned. The blob detection typically has a recall of ~90%, and a precision of ~30%. This means ~90% of the targets are found, and for every target found there are ~2 false positives. While this seems high, most of the false positives are in the background or far from the sharpie targets. This means that most false positives do not interfere with the matching to real image targets. After the matching, typically ~60% of the sharpie targets are correctly matched.

The second stage (refined optimization) uses the external calibration from the first stage, and uses projection as if it was the ‘ideal’ case. Typically, the second stage makes use of > 95% of the sharpie targets. Some filtering is still implemented for situations where the image is particularly dark, or makes particularly bad use of the camera’s dynamic range. Monte Carlo simulations of the external calibration routine have shown that the use of a second stage typically cuts the external calibration uncertainty in half. Since the second stage is not particularly expensive, the trade-off of additional processing time is well worth it.

It was decided to not combine sharpie targets and unpainted Kulites as targets since the addition of Kulites did not significantly reduce uncertainty, significantly increases computation time, and opens the door for significant errors. The Kulites have worse sub-pixel localization error than the sharpie targets since they roughly 1/4 the pixel area. Therefore, even with many of them, combining ~50 Kulites with ~20 sharpie targets only decreases the uncertainty by ~6% (according to the Monte Carlo simultations). However, computation time scales roughly linearly (or can be slightly super-linear due to PnP RANSAC) and so it roughly triples the refined stage’s computation time. Additionally, it is common for the sub-pixel localization routine to optimize on the wrong image feature since noise or a scratch on the model only has to be ~2 pixels in diameter to be the same size as the Kulite. With all this considered, when sharpie targets are present it is highly recommended to only use sharpie targets.

psp_process

Fig. 5 presents the functional data flow for the psp_process application. The processing is divided into three “phases”:

• Phase 0: initialization; camera calibration.

• Phase 1: camera image pixel values projected onto 3D wind tunnel model grid; conversion from image pixel values into intensity ratios; image registration.

• Phase 2: conversion from intensity ratios to pressure ratios; write final unsteady pressure ratio time-histories to file.

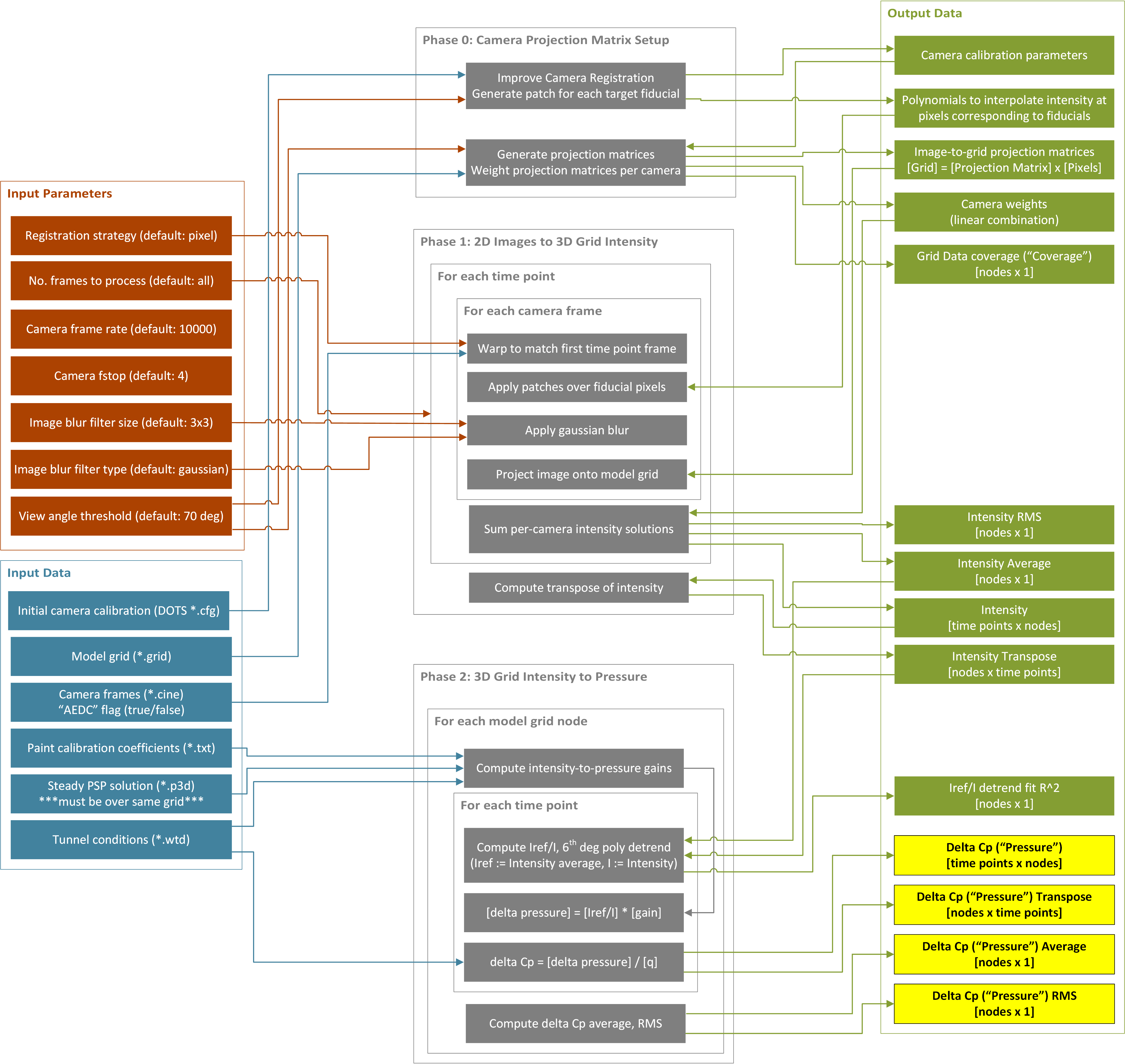
Fig. 5 psp_process functional flowchart.

Phase 1 processing

Phase 1 processing maps the camera intensity data onto the model grid using the camera-to-model registration information. Before projection, it also interpolates the intensity data over “patches” identified in the image plane corresponding to small, unpainted regions on the model surface.

The output data from Phase 1 is essentially a large matrix, or “solution”, containing the intensity value at each model node, at each frame (i.e., time step). The intensity solution is maintained in-memory between Phase 1 and Phase 2 processing, distributed across one or more computational nodes.

Steps involved are as follows:

1. A projection matrix is developed for each camera that maps pixels from the first camera frame onto the model grid nodes, starting with the camera-to-model registration solution from Phase 0.

   1. A ray-tracing process is executed to identify and exclude portions of the model grid that are:

      • not visible to the camera, or

      • too oblique-facing relative to the camera line of sight (obliqueness threshold angle between the model normal and the camera line of sight is configurable in the Input Deck)

   2. For every grid node with data from multiple cameras, combine camera data using one of the following strategies:

      • use a linear-weighted combination of the measured value from each camera; the sum of the weights is normalized to one, and each weight is linearly proportional to the angle between the surface normal and the ray from the camera to the grid node (average_view)

      • use the measured value from the camera with the best view angle (best_view)

   3. Any grid nodes that are not visible in any camera’s first frame will be marked with NaN in the output solution.

2. For each camera, and for each camera frame:

   1. Because the model may have some small amount of motion between frames, first “warp” the image to align with the first camera frame. The warping process uses a pixel-based image registration scheme assuming affine transformations.

   2. Fill in “fiducial” marking regions with polynomial patches from Phase 0. Note that the same pixel coordinates can be used for the polynomial patches for all frames because the previous step aligns each frame with the first frame.

   3. Apply the projection matrix to the aligned-and-patched image frame, to obtain the model grid node intensity values.

   4. For each time frame, sum the intensity values over each camera using the previously established weighting strategy.

Phase 2 processing

Phase 2 processing maps the Phase 1 intensity solution to an equivalent solution in physical pressure units.

Currently the only method for converting intensity to pressure that has been implemented in the software is the method devised at Arnold Engineering Development Complex (AEDC) that uses pre-test paint calibrations and the steady state PSP solutions.

The gain is computed at each grid node with Equation (1), where \(T\) is the surface temperature in \(^{\circ}F\) and \(P_{ss}\) is the steady state PSP pressure in psf. The coefficients (a-f) are specified in the paint calibration file.

(1)\[Gain = a + bT + cT^2 + (d + eT + fT^2) P_{ss}\]

The surface temperature is estimated to be the equilibrium temperature. This calculation is shown in Equation (2), where \(T_0\) is the stagnation temperature, \(T_{\infty}\) is the freestream temperature, and \(r\) is the turbulent boundary-layer recovery factor (0.896), given by Schlichting.

(2)\[T = r(T_0 - T_{\infty}) + T_{\infty}\]

Before applying the gain, the data is detrended by fitting a 6\(^{th}\)-order polynomial curve to the ratio of the average intensity over intensity for each grid node. Then, the pressure is just the AC signal times the \(Gain\). This process is shown in Equations (3), where \(f\) is a frame number, \(n\) is a grid node, \(I\) is the intensity, and \(\bar{q}\) is the dynamic pressure in psf.

(3)\[\begin{split}\begin{aligned} \bar{I}_n &= \sum_{f=1}^F I_{f,n} \\ \nonumber I_{f,n}\prime &= \bar{I}_n / I_{f,n} \\ \nonumber I_{fit}(n) &= poly\_fit(I_n\prime) \\ \nonumber I_{fit}(f,n) &= poly\_val(I_{fit}(n), f) \\ \nonumber P_{f,n} &= (I_{f,n}\prime - I_{fit}(f,n)) * Gain \\ \nonumber \Delta C_p(f,n) &= P_{f,n} * 12 * 12 / \bar{q} \\ \nonumber \end{aligned}\end{split}\]

FIDUCIAL PATCHING

1. Interpolate the camera pixel data to “patch” over small, unpainted areas on the model surface. These small areas are referred to as “fiducials” and may correspond to registration targets from the previous step as well as to other known visible elements such as blemishes, mechanical fasteners, etc.

   The interpolation process relies on the following inputs:

   • Known locations and circular diameters for each fiducial on the model surface

   • An updated camera calibration from the previous step

   The interpolation process is defined as follows:

   1. Using the updated camera calibration, project all fiducials onto the first camera frame. Ignore any points that are either:

      • Occluded by other features

      • Oblique by more than \(oblique\_angle + 5^{\circ}\) (i.e., the angle between the surface normal and the ray from the camera to the node is less than \(180^{\circ} - (oblique\_angle + 5^{\circ})\))

   2. Estimate the size of the fiducial in pixels using projection and the defined 3D fiducial size.

   3. Cluster fiducials so that no coverage patch overlaps another fiducial.

   4. Define the boundary of each cluster as \(bound\_pts\) rows of pixels outside the cluster with \(buffer\_pts\) row of pixel as a buffer.

   5. Define a threshold below which the data is either background or very poor:

      1. Compute a histogram of intensities for frame 1.

      2. Find the first local minimum after the first local maximum in the histogram. This plus \(5^{\circ}\) is the threshold.

   6. Remove any boundary pixels that are within 2 pixels of a pixel that is below the threshold.

   7. Fit a 3\(^{rd}\) order 2D polynomial to the boundary pixels of each cluster, then the interior (patched pixels) are set by evaluating the polynomial.

Memory usage and scalability

The intensity-time history and pressure-time history data are usually prohibitively large to be loaded in their entirety into the memory of a single computer (for example, for approximately 1 million grid nodes and 40,000 camera frames, each time history solution requires approximately 150 GB). Without usage of parallel processing over multiple computational nodes, the processing would need to process “blocks” of the solution and write the output to disk periodically to operate within the constraints of a single computer’s available memory.

Instead, to greatly increase speed of processing, the psp_process application is designed to execute across an arbitrary number of computational nodes. In practice, for current test data sets, the application is executed across approximately 20-50 computational nodes using the NASA Advanced Supercomputing (NAS) Pleiades cluster. The software leverages the Message Passing Toolkit (MPT) implementation provided by the Pleiades cluster, and its execution environment is controlled by the NAS-maintained Portable Batch System (PBS).

The conceptual layout of the data items manipulated during the three processing phases is shown in Fig. 6. Each large time history is divided into a series of “blocks” based on the number of available computational nodes, or “ranks.” MPT is leveraged for communication between ranks for the following operations:

• Computing sums or averages over the entire time history.

• Computing the transpose of each time history.

Fig. 6 psp_process memory model.

Phase 0 processing operations are duplicated identically across each rank for simplicity, because they do not scale with the number of camera frames.

The design decision to divide the processing into three phases was driven primarily by considerations of computational complexity and ease-of-validation. Previously, the uPSP software prototype phases were divided into separate applications to facilitate partial processing and caching of intermediate data products. The operations performed in Phase 0 could be run standalone in order to check camera registration outputs, and the intensity ratio outputs from Phase 1 could be analyzed prior to Phase 2 operations for qualitative checks of frequency content of the uPSP measurement data (conversion to pressure ratios is a scaling operation that does not affect time-varying or frequency content). In addition, the Phase 1 and Phase 2 operations are computationally intense; previous software versions were deployable to a personal laptop or desktop computer without massive parallelization, however, the processing required several orders of magnitude more time to complete than with the current parallelized code.

Choice of software language(s)

All aspects of the external calibration pipeline were written in Python, with the exception of the BVH which uses legacy C++ code (written by Tim Sandstrom) and a Python binding for ease of use.

Python 3 was selected due to developer expertise and the availability and maturity of scientific and image processing modules such as OpenCV, Tensorflow, Numpy, and Scipy. These modules are primarily written in C, C++, and Fortran with Python bindings. This allows for a user-friendly development environment where developers have expertise for quick turnaround time, while retaining fast underlying operations.