TrickLogo

Home → Tutorial Home → Numerical Integration

State Propagation with Numerical Integration

Contents

How Trick Does Numerical Integration

The type of model that we created in the last section relied on the fact that the cannon ball problem has a closed-form solution from which we can immediately calculate the cannon ball state [position, velocity] at any arbitrary time. In real-world simulation problems, this will almost never be the case.

In this section we will model the cannon ball using numeric integration, a technique that can be used when no closed-form solution exists. Instead of calculating state(n) by simply evaluating a function, it will be calculated by integrating the state time derivatives [velocity, acceleration] over the simulation time step from t(n-1) to t(n); adding that to the previous state(n-1).

The Trick integration scheme allows one to choose from amongst several well-known integration algorithms, such as Euler, Runge Kutta 2, Runge Kutta 4, and others. To provide simulation developers with a means of getting data into and out of these algorithms, Trick defines the following two job classes:

  1. derivative class jobs - for calculating the state time derivatives.
  2. integration class jobs - for integrating the state time derivatives from time t(n-1) to t(n), to produce the next state.

A special integ_loop job scheduler coordinates the calls to these jobs. Depending on the chosen integration algorithm, these jobs are called one or more times per integration time step. For the Euler integration algorithm, they are each only called once. For Runge Kutta 4 integration algorithm they are each called 4 times per integration time step.

Derivative Class Jobs

The purpose of a derivative class job is to generate model time derivatives when it is called by the integration loop scheduler. If these derivatives are dependent on the results of the corresponding integration, then they and the time dependent quantities on which they depend should be calculated in the derivative job.

For "F=ma" type models, derivative jobs calculate acceleration, by dividing the sum of the forces applied to the object, whose state we are propagating, at a given time, by its mass.

If acceleration is constant, then it does not really need to be calculated in a derivative job. But if acceleration is a function of time, as when it is a function of one or more of the model state variables, then it needs to be calculated in a derivative job. Note that the time dependent quantities from which acceleration is calculated should also be calculated in the derivative job.

In the corresponding integration class job, the acceleration is then integrated to produce velocity, and velocity is integrated to produce position.

Example: A Skydiver

Suppose we want to model a skydiver plummeting to Earth. In our model we decide to account for two forces that are acting on the skydiver:

  1. The force of gravity.
  2. The atmospheric drag force.

The force of gravity can be calculated using Newton's Law of Gravitation:

Figure 1 - Newton's Law of Gravitation

and the drag force can be calculated using the drag equation:

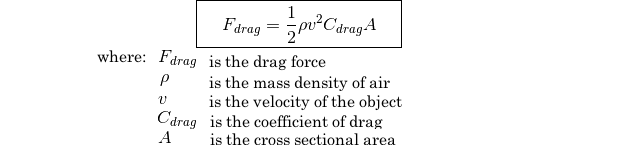
Figure 2 - Drag Equation

Notice that the force of gravity is dependent upon the skydiver position, which is an integration result. Therefore the force of gravity needs to be calculated in the derivative class job, prior to summing the forces.

Similarly, the drag force has state variable dependencies. It is obviously dependent on velocity, but also notice that the atmospheric air density is a function of altitude (position). So, it too should be calculated in the derivative job.

Again, if the derivatives are dependent on the results of the corresponding integration, then those derivatives and the time dependent quantities on which they depend should be calculated in the derivative job.

Integration Class Jobs

The purpose of a integration class job is to integrate the derivatives that were calculated in the corresponding derivative jobs, producing the next simulation state from the previous state.

Integration jobs generally look very similar. That is because they are expected to do the same five things:

  1. Load the state into the integrator.
  2. Load the state derivatives into the integrator.
  3. Call the integrate() function.
  4. Unload the updated state from the integrator.
  5. Return the value that was returned by the integrate() call.

Using the integration interface functions, load_state(), load_deriv(), integrate(), and unload_state() requires that integrator_c_intf.h be included. And of course the data structure(s) that define the model state will also have to be included.

The value returned from integrate(), and stored in the ipass variable below, tells the Trick integration scheduler the status of the state integration. It returns the last integration step number until it is finished, when it returns 0. For example, if the integrator is configured for Runge Kutta 4, a four step integration algorithm, then integrate() will return 1 the first time it is called, 2 the second time, 3 the third, and 0 the fourth time, indicating that it is done.

Configuring The Integration Scheduler

Producing simulation states by numerical integration requires that the derivative and integration jobs be called at the appropriate rate and times. This requires a properly configured integration scheduler.

First, instantiate an integration scheduler in the S_define with a declaration of the following form:

IntegLoop integLoopName ( integrationTimeStep ) listOfSimObjectNames ;

Then, in the input file, call the IntegLoop getIntegrator() method to specify the integration algorithm of choice and the number of state variables to be integrated.

integLoopName.getIntegrator( algorithm, N );

Updating the Cannonball Sim to use Numerical Integration

Rather than type everything again, we will first "tidy up" and then copy the simulation. When trick-CP builds a simulation, it creates a makefile, that directs the build process. The generated makefile also contains a procedure ("target" in Make parlance) called "spotless" for removing all of the intermediate files that were produced during the build but that are not longer needed.

So, to tidy up, execute the following:

% cd $HOME/trick_sims/SIM_cannon_analytic
% make spotless

And then copy the sim directory.

% cd ..
% cp -r SIM_cannon_analytic SIM_cannon_numeric

Create cannon_numeric.h.

In this new simulation, we're going to create two new functions, 1) cannon_deriv() [our derivative job], and 2) cannon_integ () [our integration job]. We'll put prototypes for each these functions into cannon_numeric.h. This new header file which will replace cannon_analytic.h.

Listing - cannon_numeric.h 

/*************************************************************************
PURPOSE: ( Cannonball Numeric Model )
**************************************************************************/

#ifndef CANNON_NUMERIC_H
#define CANNON_NUMERIC_H

#include "cannon.h"

#ifdef __cplusplus
extern "C" {
#endif
int cannon_integ(CANNON*) ;
int cannon_deriv(CANNON*) ;
#ifdef __cplusplus
}
#endif
#endif

% cd SIM_cannon_numeric/models/cannon/include
% vi cannon_numeric.h <edit and save>

Create cannon_numeric.c.

Header and Includes for cannon_numeric.c 

/*********************************************************************
  PURPOSE: ( Trick numeric )
*********************************************************************/
#include <stddef.h>
#include <stdio.h>
#include "trick/integrator_c_intf.h"
#include "../include/cannon_numeric.h"

Creating a Derivative Class Job

In the case of the cannon ball sim, we are making numerous simplifications, like assuming that the acceleration of gravity is constant (in real life, it is not) and ignoring aerodynamic drag. This means that our cannon ball simulation is not as accurate as it might be, but for our purposes here, which is to teach how to use Trick, it should be fine.

Listing - cannon_deriv()

int cannon_deriv(CANNON* C) {

    if (!C->impact) {
        C->acc[0] = 0.0 ;
        C->acc[1] = -9.81 ;
    } else {
        C->acc[0] = 0.0 ;
        C->acc[1] = 0.0 ;
    }
    return(0);
}

👉 Add cannon_deriv() to cannon_numeric.c.

Creating an Integration Class Job

For our cannon ball sim, our integration job needs to:

  1. Load the cannon ball state ( pos[] and vel[] ) into the integrator.
  2. Load the cannon ball state derivatives ( vel[] and acc[] )into the integrator.
  3. Call the integrate() function.
  4. Unload the updated state from the integrator into pos[] and vel[].
  5. Return the value that was returned by the integrate() call.

IMPORTANT:

The functions load_state(), load_deriv(), and unload_state() take a variable number of parameters. When calling these functions, the last parameter MUST ALWAYS BE NULL. The NULL value marks the end of the parameter list. Forgetting the final NULL will likely cause the simulation to crash and ... It won't be pretty.

Listing - cannon_integ()

int cannon_integ(CANNON* C) {
    int ipass;

    load_state(
        &C->pos[0] ,
        &C->pos[1] ,
        &C->vel[0] ,
        &C->vel[1] ,
        NULL);

    load_deriv(
        &C->vel[0] ,
        &C->vel[1] ,
        &C->acc[0] ,
        &C->acc[1] ,
        NULL);

    ipass = integrate();

    unload_state(
        &C->pos[0] ,
        &C->pos[1] ,
        &C->vel[0] ,
        &C->vel[1] ,
        NULL );

    return(ipass);
}

👉 Add cannon_integ() to cannon_numeric.c.

Updating the S_define File

Next, our S_define file needs to be updated.

Update LIBRARY DEPENDENCIES

In the LIBRARY_DEPENDENCY section, replace: (cannon/src/cannon_analytic.c) with (cannon/src/cannon_numeric.c).

Update ##include Header File

Replace:

##include "cannon/include/cannon_analytic.h"

with:

##include "cannon/include/cannon_numeric.h"

Update Scheduled Jobs

Replace:

(0.01, "scheduled") cannon_analytic( &cannon ) ;

with:

   ("derivative") cannon_deriv( &cannon ) ;
   ("integration") trick_ret= cannon_integ( & cannon ) ;

Add Integration Scheduler and Integrator

To the bottom of the S_define file, add:

IntegLoop dyn_integloop (0.01) dyn ;
void create_connections() {
    dyn_integloop.getIntegrator(Runge_Kutta_4, 4);
}

The first line here defines an integration scheduler called dyn_integloop that executes derivative and integration jobs in the dyn SimObject. The integration rate is specified in parentheses.

create_connections is a special function-like construct whose code is copied into S_source.cpp and is executed directly after SimObject instantiations. Common uses are to 1) instantiate integrators, and 2) connect data structures between SimObjects.

dyn_integloop.getIntegrator configures our integration scheduler. Its first argument specifies the integration algorithm to be used. In the case Runge_Kutta_4. The second argument is the number of variables that are to be integrated. There are four variables for this simulation (pos[0], pos[1], vel[0], vel[1]).

The updated S_define is:

Listing - S_define

/****************************************************************
PURPOSE: (S_define file for SIM_cannon_numeric)
LIBRARY_DEPENDENCY: ((cannon/src/cannon_init.c)
                     (cannon/src/cannon_numeric.c)
                     (cannon/src/cannon_shutdown.c))
****************************************************************/
#include "sim_objects/default_trick_sys.sm"
##include "cannon/include/cannon_numeric.h"

class CannonSimObject : public Trick::SimObject {
    public:
    CANNON cannon ;
    CannonSimObject() {
        ("initialization") cannon_init( &cannon ) ;
        ("default_data") cannon_default_data( &cannon ) ;
        ("derivative") cannon_deriv( &cannon ) ;
        ("integration") trick_ret= cannon_integ( &cannon ) ;
        ("shutdown") cannon_shutdown( &cannon ) ;
    }
};

CannonSimObject dyn ;
IntegLoop dyn_integloop (0.01) dyn ;
void create_connections() {
    dyn_integloop.getIntegrator(Runge_Kutta_4, 4);
}

Running The Cannonball With Trick Integration

There is nothing different about running with Trick integration. We just need to build the simulation and run it.

% cd $HOME/trick_sims/SIM_cannon_numeric
% trick-CP

If the sim builds successfully, then run it.

% ./S_main*exe RUN_test/input.py &

Run the simulation to completion

Numeric Versus Analytical

Let's compare the analytical "perfect" simulation with latest version using Trick integration.

  1. Start the trick data products: % trick-dp &. There should be the two SIMs in the "Sims/Runs" pane of trick-dp:

    1. SIM_cannon_analytic, and
    2. SIM_cannon_numeric.

  2. Double click SIM_cannon_analytic->RUN_test This will move SIM_cannon_analytic/RUN_test to the selection box.

  3. Double click SIM_cannon_numeric->RUN_test Now the two RUNs we wish to compare will be present in the selection box.

  4. Double click SIM_cannon_analytic/DP_cannon_xy DP_cannon_xy will be moved into the selection box.

  5. Click the Co-Plot button (collated white sheets icon) located on the menu bar. Voila! The curves appear the same, but there is a slight difference. Living with less than a billionth of a meter difference will not cause us to lose sleep. However, we still dont like it! It is no fun being a sloppy perfectionist!

Congratulations, you are now running a simulation with numerical integration.

Next Page

This site is open source. Improve this page.