1. Introduction
This document describes F Prime Prime, also known as FPP or F Double Prime. FPP is a modeling language for the F Prime flight software framework. For more detailed information about F Prime, see the F Prime User Manual.
The goals of FPP are as follows:
-
To provide a modeling language for F Prime that is simple, easy to use, and well-tailored to its purpose.
-
To provide semantic checking and error reporting for F Prime models.
-
To generate code in the various languages that F Prime uses, e.g., C++ and JSON. In this document, we will call these languages the target languages.
Developers may combine code generated from FPP with code written by hand to create, e.g., deployable flight software (FSW) programs and ground data environments.
The name “F Double Prime” (or F″) deliberately suggests the idea of a “derivative” of F Prime (or F′). By “integrating” an FPP model (i.e., running the tools) you get a partial FSW implementation in the F Prime framework; and then by “integrating” again (i.e., providing the project-specific C++ implementation) you get a FSW application.
Purpose: The purpose of this document is to describe FPP in a way that is accessible to users, including beginning users. A more detailed and precise description is available in The FPP Language Specification. We recommend that you read this document before consulting that one.
Overview: The rest of this document proceeds as follows. Section 2 explains how to get up and running with FPP. Sections 3 through 12 describe the elements of an FPP model, starting with the simplest elements (constants and types) and working towards the most complex (components and topologies). Section 13 explains how to specify a model as a collection of files: for example, it covers the management of dependencies between files. Section 14 explains how to analyze FPP models and how to translate FPP models to C++ and JSON. It also explains how to translate an XML format previously used by F Prime into FPP. Section 15 explains how to write a C++ implementation against the code generated from an FPP model.
2. Installing FPP
Before reading the rest of this document, you should install the latest version of FPP. The installation instructions are available here:
Make sure that the FPP command-line tools are in your shell path.
For example, running fpp-check on the command line should succeed and should
prompt for standard input. You can type control-C to end
the program:
% fpp-check ^C %
fpp-check is the tool for checking that an FPP model is valid.
Like most FPP tools,
fpp-check reads either from named files or from standard input.
If one or more files are named on the command line, fpp-check reads those;
otherwise it reads from standard input.
As an example, the following two operations are equivalent:
% fpp-check < file.fpp % fpp-check file.fpp
The first operation redirects file.fpp into the standard input of
fpp-check.
The second operation names file.fpp as an input file of fpp-check.
Most of the examples in the following sections are complete FPP models.
You can run the models through
fpp-check by typing or pasting them into a file or into standard input.
We recommend that you to this for at least a few of the examples,
to get a feel for how FPP works.
3. Defining Constants
The simplest FPP model consists of one or more constant definitions. A constant definition associates a name with a value, so that elsewhere you can use the name instead of re-computing or restating the value. Using named constants makes the model easier to understand (the name says what the value means) and to maintain (changing a constant definition is easy; changing all and only the relevant uses of a repeated value is not).
This section covers the following topics:
-
Writing an FPP constant definition.
-
Writing an expression, which is the source text that defines the value associated with the constant definition.
-
Writing multiple constant definitions.
-
Writing a constant definition that spans two or more lines of source text.
3.1. Writing a Constant Definition
To write a constant definition, you write the keyword constant,
an equals sign, and an expression.
A later section
describes all the expressions you can write.
Here is an example that uses an integer literal expression representing
the value 42:
constant ultimateAnswer = 42This definition associates the name ultimateAnswer with the value 42.
Elsewhere in the FPP model you can use the name ultimateAnswer to represent
the value.
You can also generate a C++ header file that defines the C++ constant
ultimateAnswer and gives it the value 42.
As an example, do the following:
-
On the command line, run
fpp-check. -
When the prompt appears, type the text shown above, type return, type control-D, and type return.
You should see something like the following on your console:
% fpp-check constant ultimateAnswer = 42 ^D %
As an example of an incorrect model that produces an error message, repeat the exercise, but omit the value 42. You should see something like this:
% fpp-check constant ultimateAnswer = ^D fpp-check stdin: end of input error: expression expected
Here the fpp-check tool is telling you that it could not parse the input:
the input ended where it expected an expression.
3.2. Names
Names in FPP follow the usual rules for identifiers in a programming language:
-
A name must contain at least one character.
-
A name must start with a letter or underscore character.
-
The characters after the first may be letters, numbers, or underscores.
For example:
-
name,Name,_name, andname1are valid names. -
1invalidis not a valid name, because names may not start with digits.
3.2.1. Reserved Words
Certain sequences of letters such as constant are called out as reserved
words (also called keywords) in FPP.
Each reserved word has a special meaning, such as introducing a constant
declaration.
The FPP Language Specification has a complete list of reserved words.
In this document, we will introduce reserved words as needed to explain
the language features.
Using a reserved word as a name in the ordinary way causes a parsing error. For example, this code is incorrect:
constant constant = 0To use a reserved word as a name, you must put the character $ in
front of it with no space.
For example, this code is legal:
constant $constant = 0The character sequence $constant represents the name constant,
as opposed to the keyword constant.
You can put the character $ in front of any identifier,
not just a keyword.
If the identifier is not a keyword, then the $ has no effect.
For example, $name has the same meaning as name.
3.2.2. Name Clashes
FPP will not let you define two different symbols of the same kind with the same name. For example, this code will produce an error:
constant c = 0
constant c = 1Two symbols can have the same unqualified name if they reside in different modules or enums; these concepts are explained below. Two symbols can also have the same name if the analyzer can distinguish them based on their kinds. For example, an array type (described below) and a constant can have the same name, but an array type and a struct type may not. The FPP Language Specification has all the details.
3.3. Expressions
This section describes the expressions that you can write as part of a constant definition. Expressions appear in other FPP elements as well, so we will refer back to this section in later sections of the manual.
3.3.1. Primitive Values
A primitive value expression represents a primitive machine value, such as an integer. It is one of the following:
-
A decimal integer literal value such as
1234. -
A hexadecimal integer literal value such as
0xABCDor0xabcd. -
A floating-point literal value such as
12.34or1234e-2. -
A Boolean literal expression
trueorfalse.
As an exercise, construct some constant definitions with primitive values as their
expressions, and
feed the results to fpp-check.
For example:
constant a = 1234
constant b = 0xABCDIf you get an error, make sure you understand why.
3.3.2. String Values
A string value represents a string of characters. There are two kinds of string values: single-line strings and multiline strings.
Single-line strings:
A single-line string represents a string of characters
that does not contain a newline character.
It is written as a string of characters enclosed in double quotation
marks ".
For example:
constant s = "This is a string."To put the double-quote character in a string, write the double quote
character as \", like this:
constant s = "\"This is a quotation within a string,\" he said."To encode the character \ followed by the character ", write
the backslash character as \\, like this:
constant s = "\\\""This string represents the literal character sequence \, ".
In general, the sequence \ followed by a character c
is translated to c.
This sequence is called an escape sequence.
Multiline strings:
A multiline string represents a string of characters
that may contain a newline character.
It is enclosed in a pair of sequences of three double quotation
marks """.
For example:
constant s = """
This is a multiline string.
It has three lines.
"""When interpreting a multiline string, FPP ignores any newline
characters at the start and end of the string.
FPP also ignores any blanks to the left of the column where
the first """ appears.
For example, the string shown above consists of three lines and starts
with This.
Literal quotation marks are allowed inside a multiline string:
constant s = """
"This is a quotation within a string," he said.
"""Escape sequences work as for single-line strings. For example:
constant s = """
Here are three double-quote characters in a row: \"\"\"
"""3.3.3. Array Values
An array value expression represents a fixed-size array of values. To write an array value expression, you write a comma-separated list of one or more values (the array elements) enclosed in square brackets. Here is an example:
constant a = [ 1, 2, 3 ]This code associates the name a with the array of
integers
[ 1, 2, 3 ].
As mentioned in the introduction, an FPP model describes the structure of a FSW application; the computations are specified in a target language such as C++. As a result, FPP does not provide an array indexing operation. In particular, it does not specify the index of the leftmost array element; that is up to the target language. For example, if the target language is C++, then array indices start at zero.
Here are some rules for writing array values:
-
An array value must have at least one element. That is,
[]is not a valid array value. -
The types of the elements must match. For example, the following code is illegal, because the value
1(which has typeInteger) and the value"abcd"(which has typestring) are incompatible:constant mismatch = [ 1, "abcd" ]Try entering this example into
fpp-checkand see what happens.
What does it mean for types to match? The FPP Specification has all the details, and we won’t attempt to repeat them here. In general, things work as you would expect: for example, we can convert an integer value to a floating-point value, so the following code is allowed:
constant a = [ 1, 2.0 ]It evaluates to an array of two floating-point values.
If you are not sure whether a type conversion is allowed, you can
ask fpp-check.
For example: can we convert a Boolean value to an integer value?
In older languages like C and C++ we can, but in many newer languages
we can’t. Here is the answer in FPP:
% fpp-check
constant a = [ 1, true ]
^D
fpp-check
stdin: 1.16
constant a = [ 1, true ]
^
error: cannot compute common type of Integer and bool
So no, we can’t.
Here are two more points about array values:
-
Any legal value can be an element of an array value, so in particular arrays of arrays are allowed. For example, this code is allowed:
constant a = [ [ 1, 2 ], [ 3, 4 ] ]It represents an array with two elements: the array
[ 1, 2 ]and the array[ 3, 4 ]. -
To avoid repeating values, a numeric, string, or Boolean value is automatically promoted to an array of appropriate size whenever necessary to make the types work. For example, this code is allowed:
constant a = [ [ 1, 2, 3 ], 0 ]It is equivalent to this:
constant a = [ [ 1, 2, 3 ], [ 0, 0, 0 ] ]
3.3.4. Array Elements
An array element expression represents an element of an array value. To write an array element expression, you write an array value followed by an index expression enclosed in square brackets. The index expression must resolve to a number. The number specifies the index of the array element, where the array indices start at zero.
Here is an example:
constant a = [ 1, 2, 3 ]
constant b = a[1]In this example, the constant b has the value 2.
The index expression must resolve to a number that is in range
for the array.
For example, this code is incorrect, because "hello" is not a number:
constant a = [ 1, 2, 3 ]
constant b = a["hello"]This code is incorrect because 3 is not in the range [0, 2]:
constant a = [ 1, 2, 3 ]
constant b = a[3]3.3.5. Struct Values
A struct value expression represents a C- or C++-style structure, i.e., a mapping of names to values. To write a struct value expression, you write a comma-separated list of zero or more struct members enclosed in curly braces. A struct member consists of a name, an equals sign, and a value.
Here is an example:
constant s = { x = 1, y = "abc" }This code associates the name s with a struct value.
The struct value has two members x and y.
Member x has the integer value 1, and member y has the string value "abc".
The order of members: When writing a struct value, the order in which the
members appear does not matter.
For example, in the following code, constants s1 and s2 denote the same
value:
constant s1 = { x = 1, y = "abc" }
constant s2 = { y = "abc", x = 1 }The empty struct: The empty struct is allowed:
constant s = {}Arrays in structs: You can write an array value as a member of a struct value. For example, this code is allowed:
constant s = { x = 1, y = [ 2, 3 ] }Structs in arrays: You can write a struct value as a member of an array value. For example, this code is allowed:
constant a = [ { x = 1, y = 2 }, { x = 3, y = 4 } ]This code is not allowed, because the element types don’t match — an array is not compatible with a struct.
constant a = [ { x = 1, y = 2 }, [ 3, 4 ] ]However, this code is allowed:
constant a = [ { x = 1, y = 2 }, { x = 3 } ]Notice that the first member of a is a struct with two members x and y.
The second member of a is also a struct, but it has only one member x.
When the FPP analyzer detects that a struct type is missing a member,
it automatically adds the member, giving it a default value.
The default values are the ones you would expect: zero for numeric members, the empty
string for string members, and false for Boolean members.
So the code above is equivalent to the following:
constant a = [ { x = 1, y = 2 }, { x = 3, y = 0 } ]3.3.6. Struct Members
A struct member expression represents a member of a struct value. To write a struct member expression, you write a struct value followed by a dot and the member name. For example:
constant a = { x = 1, y = [ 2, 3 ] }
constant b = a.yHere a is a struct value with members x and y
The constant b has the array value [ 2, 3 ], which is the
value stored in member y of a.
This code is incorrect because a is not a struct value:
constant a = 0
constant b = a.yThis code is incorrect because z is not a member of a:
constant a = { x = 1, y = [ 2, 3 ] }
constant b = a.z3.3.7. Name Expressions
A name expression is a use of a name appearing in a constant definition. It stands for the associated constant value. For example:
constant a = 1
constant b = aIn this code, constant b has the value 1.
The order of definitions does not matter, so this code is equivalent:
constant b = a
constant a = 1The only requirement is that there may not be any cycles in the graph
consisting of constant definitions and their uses.
For example, this code is illegal, because there is a cycle from a to b to
c and back to a:
constant a = c
constant b = a
constant c = bTry submitting this code to fpp-check, to see what happens.
Names like a, b, and c are simple or unqualified names.
Names can also be qualified: for example A.a is allowed.
We will discuss qualified names further when we introduce
module definitions and enum definitions below.
3.3.8. Value Arithmetic Expressions
A value arithmetic expression performs arithmetic on values. It is one of the following:
-
A negation expression, for example:
constant a = -1 -
A binary operation expression, where the binary operation is one of
+(addition),-(subtraction),*(multiplication), and/(division). For example:constant a = 1 + 2 -
A parenthesis expression, for example:
constant a = (1)
The following rules apply to arithmetic expressions:
-
The subexpressions must be integer or floating-point values.
-
If there are any floating-point subexpressions, then the entire expression is evaluated using 64-bit floating-point arithmetic.
-
Otherwise the expression is evaluated using arbitrary-precision integer arithmetic.
-
In a division operation, the second operand may not be zero or (for floating-point values) very close to zero.
3.3.9. Compound Expressions
Wherever you can write a value inside an expression, you can write a more complex expression there, so long as the types work out. For example, these expressions are valid:
constant a = (1 + 2) * 3
constant b = [ 1 + 2, 3 ]The first example is a binary expression whose first operand is a parentheses expression; that parentheses expression in turn has a binary expression as its subexpression. The second example is an array expression whose first element is a binary expression.
This expression is invalid, because 1 + 2.0 evaluates to a floating-point
value, which is incompatible with type string:
constant a = [ 1 + 2.0, "abc" ]Compound expressions are evaluated in the obvious way. For example, the constant definitions above are equivalent to the following:
constant a = 9
constant b = [ 3, 3 ]For compound arithmetic expressions, the precedence and associativity rules are the usual ones (evaluate parentheses first, then multiplication, and so forth).
3.4. Multiple Definitions and Element Sequences
Typically you want to specify several definitions in a model source file, not just one. There are two ways to do this:
-
You can separate the definitions by one or more newlines, as shown in the examples above.
-
You can put the definitions on the same line, separated by a semicolon.
For example, the following two code excerpts are equivalent:
constant a = 1
constant b = 2constant a = 1; constant b = 2More generally, a collection of several constant definitions is an example of an element sequence, i.e., a sequence of similar syntactic elements. Here are the rules for writing an element sequence:
-
Every kind of element sequence has optional terminating punctuation. The terminating punctuation is either a semicolon or a comma, depending on the kind of element sequence. For constant definitions, it is a semicolon.
-
When writing elements on separate lines, the terminating punctuation is optional.
-
When writing two or more elements on the same line, the terminating punctuation is required between the elements and optional after the last element.
3.5. Multiline Definitions
Sometimes, especially for long definitions, it is useful to split a definition across two or more lines. In FPP there are several ways to do this.
First, FPP ignores newlines that follow opening symbols like [ and precede
closing symbols like ].
For example, this code is allowed:
constant a = [
1, 2, 3
]Second, the elements of an array or struct form an element sequence (see the previous section), so you can write each element on its own line, omitting the commas if you wish:
constant s = {
x = 1
y = 2
z = 3
}This is a clean way to write arrays and structs.
The assignment of each element to its own line and the lack of
terminating punctuation
make it easy to rearrange the elements.
In particular, one can do a line-by-line sort on the elements (for example, to
sort struct members alphabetically by name) without concern for messing up the
arrangement of commas.
If we assume that the example represents the first five lines of a source file,
then in vi this is easily done as :2-4!sort.
Third, FPP ignores newlines that follow connecting symbols such as = and +
For example, this code is allowed;
constant a =
1
constant b = 1 +
2Finally, you can always create an explicit line continuation by escaping
one or more newline characters with \:
constant \
a = 1Note that in this example you need the explicit continuation, i.e., this code is not legal:
constant
a = 13.6. Framework Constants
Certain constants defined in FPP have a special meaning in the
F Prime framework.
These constants are called framework constants.
For example, the constant FW_FIXED_LENGTH_STRING_SIZE
defines the default maximum size of a string.
(We will define string types
in a later section of this
manual.)
You typically set these constants by overriding configuration
files provided in the directory default/config in the F Prime repository.
For example, the file default/config/FpConstants.fpp provides a default
definition for FW_FIXED_LENGTH_STRING_SIZE.
You can override this default value by a different definition for this
constant.
The
F
Prime User Manual
explains how to do this configuration.
The FPP analyzer does not require that framework constants be defined
unless they are used.
For example, the following model is valid, because it neither defines nor users
FW_FIXED_LENGTH_STRING_SIZE:
constant a = 0The following model is valid because it defines and uses FW_FIXED_LENGTH_STRING_SIZE:
constant FW_FIXED_LENGTH_STRING_SIZE = 80
constant a = FW_FIXED_LENGTH_STRING_SIZEThe following model is invalid, because it uses FW_FIXED_LENGTH_STRING_SIZE
without defining it:
constant a = FW_FIXED_LENGTH_STRING_SIZEIf framework constants are defined in the FPP model, then
then they must conform to certain rules.
These rules are spelled out in detail in the
The
FPP Language Specification.
For example, FW_FIXED_LENGTH_STRING_SIZE must have an integer type.
So this model is invalid:
constant FW_FIXED_LENGTH_STRING_SIZE = "abc"Here is what happens when you run this model through fpp-check:
% fpp-check constant FW_FIXED_LENGTH_STRING_SIZE = "abc" ^D fpp-check stdin:1.1 constant FW_FIXED_LENGTH_STRING_SIZE = "abc" ^ error: the F Prime framework constant FW_FIXED_LENGTH_STRING_SIZE must have an integer type
4. Writing Comments and Annotations
In FPP, you can write comments that are ignored by the parser. These are just like comments in most programming languages. You can also write annotations that have no meaning in the FPP model but are attached to model elements and may be carried through to translation — for example, they may become comments in generated C++ code.
4.1. Comments
A comment starts with the character # and goes to the end of the line.
For example:
# This is a commentTo write a comment that spans multiple lines, start each line with #:
# This is a comment.
# It spans two lines.4.2. Annotations
Annotations are attached to elements of a model, such as constant definitions. A model element that may have an annotation attached to it is called an annotatable element. Any constant definition is an annotatable element. Other annotatable elements will be called out in future sections of this document.
There are two kinds of annotations: pre annotations and post annotations:
-
A pre annotation starts with the character
@and is attached to the annotatable element that follows it. -
A post annotation starts with the characters
@<and is attached to the annotatable element that precedes it.
In either case
-
Any white space immediately following the
@or@<characters is ignored. -
The annotation goes to the end of the line.
For example:
@ This is a pre annotation
constant c = 0 @< This is a post annotationMultiline annotations are allowed. For example:
@ This is a pre annotation.
@ It has two lines.
constant c = 0 @< This is a post annotation.
@< It also has two lines.The meaning of the annotations is tool-specific. A typical use is to
concatenate the pre and post annotations into a list of lines and emit them as
a comment. For example, if you send the code immediately above through the
tool fpp-to-cpp,
it should generate a file FppConstantsAc.hpp. If you examine that file,
you should see, in relevant part, the following code:
//! This is a pre annotation.
//! It has two lines.
//! This is a post annotation.
//! It also has two lines.
enum FppConstant_c {
c = 0
};The two lines of the pre annotation and the two lines of the post annotation have been concatenated and written out as a Doxygen comment attached to the constant definition, represented as a C++ enum.
In the future, annotations may be used to provide additional capabilities, for example timing analysis, that are not part of the FPP language specification.
5. Defining Modules
In an FPP model, a module is a group of model elements that are all qualified with a name, called the module name. An FPP module corresponds to a namespace in C++ and a module in Python. Modules are useful for (1) organizing a large model into a hierarchy of smaller units and (2) avoiding name clashes between different units.
To define a module, you write the keyword module followed by one
or more definitions enclosed in curly braces.
For example:
module M {
constant a = 1
}The name of a module qualifies the names of all the definitions that the module
encloses.
To write the qualified name, you write the qualifier, a dot, and the base name:
for example M.a. (This is also the way that
name qualification works in Python, Java, and Scala.)
Inside the module, you can use the qualified name or the unqualified
name.
Outside the module, you must use the qualified name.
For example:
module M {
constant a = 1
constant b = a # OK: refers to M.a
constant c = M.b
}
constant a = M.a
constant c = b # Error: b is not in scope hereAs with namespaces in C++, you can close a module definition and reopen it later. All the definitions enclosed by the same name go in the module with that name. For example, the following code is allowed:
module M {
constant a = 0
}
module M {
constant b = 1
}It is equivalent to this code:
module M {
constant a = 0
constant b = 1
}You can define modules inside other modules. When you do that, the name qualification works in the obvious way. For example:
module A {
module B {
constant c = 0
}
}
constant c = A.B.cThe inside of a module definition is an element sequence with a semicolon as the optional terminating punctuation. For example, you can write this:
module M { constant a = 0; constant b = 1 }; constant c = M.aA module definition is an annotatable element, so you can attach annotations to it, like this:
@ This is module M
module M {
constant a = 0
}6. Defining Types
An FPP model may include one or more type definitions. These definitions describe named types that may be used elsewhere in the model and that may generate code in the target language. For example, an FPP type definition may become a class definition in C++.
There are four kinds of type definitions:
-
Array type definitions
-
Struct type definitions
-
Abstract type definitions
-
Alias type definitions
Type definitions may appear at the top level or inside a module definition. A type definition is an annotatable element.
6.1. Array Type Definitions
An array type definition associates a name with an array type. An array type describes the shape of an array value. It specifies an element type and a size.
6.1.1. Writing an Array Type Definition
As an example, here is an array type definition that associates
the name A with an array of three values, each of which is a 32-bit unsigned
integer:
array A = [3] U32In general, to write an array type definition, you write the following:
-
The keyword
array. -
The name of the array type.
-
An equals sign
=. -
An expression enclosed in square brackets
[…]denoting the size (number of elements) of the array. -
A type name denoting the element type. The available type names are discussed below.
Notice that the size expression precedes the element type, and the whole
type reads left to right.
For example, you may read the type [3] U32 as "array of 3 U32."
The size may be any legal expression. It doesn’t have to be a literal integer. For example:
constant numElements = 10
array A = [numElements] U326.1.2. Type Names
The following type names are available for the element types:
-
The type names
U8,U16,U32, andU64, denoting the type of unsigned integers of width 8, 16, 32, and 64 bits. -
The type names
I8,I16,I32, andI64, denoting the type of signed integers of width 8, 16, 32, and 64 bits. -
The type names
F32andF64, denoting the type of floating-point values of width 32 and 64 bits. -
The type name
bool, denoting the type of Boolean values (trueandfalse). -
The type name
string, denoting the type of string values. For example:type FwSizeStoreType = U16 constant FW_FIXED_LENGTH_STRING_SIZE = 256 # A is an array of 3 strings with size FW_FIXED_LENGTH_STRING_SIZE array A = [3] stringNotice that we defined the framework type
FwSizeStoreTypeand the framework constantFW_FIXED_LENGTH_STRING_SIZE. These definitions are required when using the typestring. Typically you provide them as part of the F Prime configuration.FwSizeStoreTypespecifies the type to use for storing the length of a string.FW_FIXED_LENGTH_STRING_SIZEspecifies the size of the buffer used to store string data. -
The type name
string sizee, where e is a numeric expression specifying the maximum string length of any value of that type. For example:type FwSizeStoreType = U16 # A is an array of 3 strings with size 40 array A = [3] string size 40Here we just specified
FwSizeStoreType. If a string type has an explicit size, then it does not use the definitionFW_FIXED_LENGTH_STRING_SIZE. -
A name associated with another type definition. In particular, an array definition may have another array definition as its element type; this situation is discussed further below.
An array type definition may not refer to itself (array type definitions are not recursive). For example, this definition is illegal:
array A = [3] A # Illegal: the definition of A may not refer to itself6.1.3. Default Values
Optionally, you can specify a default value for an array type.
To do this, you write the keyword default and an expression
that evaluates to an array value.
For example, here is an array type A with default value [ 1, 2, 3 ]:
array A = [3] U32 default [ 1, 2, 3 ]A default value expression need not be a literal array value; it can be any expression with the correct type. For example, you can create a named constant with an array value and use it multiple times, like this:
constant a = [ 1, 2, 3 ]
array A = [3] U8 default a # default value is [ 1, 2, 3 ]
array B = [3] U16 default a # default value is [ 1, 2, 3 ]If you don’t specify a default value, then the type gets an automatic default value,
consisting of the default value for each element.
The default numeric value is zero, the default Boolean value is false,
the default string value is "", and the default value of an array type
is specified in the type definition.
The type of the default expression must match the size and element type of the array, with type conversions allowed as discussed for array values. For example, this default expression is allowed, because we can convert integer values to floating-point values, and we can promote a single value to an array of three values:
array A = [3] F32 default 1 # default value is [ 1.0, 1.0, 1.0 ]However, these default expressions are not allowed:
array A = [3] U32 default [ 1, 2 ] # Error: size does not matcharray B = [3] U32 default [ "a", "b", "c" ] # Error: element type does not match6.1.4. Format Strings
You can specify an optional format string which says how to display each element value and optionally provides some surrounding text. For example, here is an array definition that interprets three integer values as wheel speeds measured in RPMs:
array WheelSpeeds = [3] U32 format "{} RPM"Then an element with value 100 would have the format 100 RPM.
Note that the format string specifies the format for an element, not the
entire array.
The way an entire array is displayed is implementation-specific.
A standard way is a comma-separated list enclosed in square brackets.
For example, a value [ 100, 200, 300 ] of type WheelSpeeds might
be displayed as [ 100 RPM, 200 RPM, 300 RPM ].
Or, since the format is the same for all elements, the implementation could
display the array as [ 100, 200, 300 ] RPM.
The special character sequence {} is called a replacement field; it says
where to put the value in the format text.
Each format string must have exactly one replacement field.
The following replacement fields are allowed:
-
The field
{}for displaying element values in their default format. -
The field
{c}for displaying a character value -
The field
{d}for displaying a decimal value -
The field
{x}for displaying a hexadecimal value -
The field
{o}for displaying an octal value -
The field
{e}for displaying a rational value in exponent notation, e.g.,1.234e2. -
The field
{f}for displaying a rational value in fixed-point notation, e.g.,123.4. -
The field
{g}for displaying a rational value in general format (fixed-point notation up to an implementation-dependent size and exponent notation for larger sizes).
For field types c, d, x, and o, the element type must be an integer
type.
For field types e, f, and g, the element type must be a floating-point
type.
For example, the following format string is illegal, because
type string is not an integer type:
array A = [3] string format "{d}" # Illegal: string is not an integer typeFor field types e, f, and g, you can optionally specify a precision
by writing a decimal point and an integer before the field type. For example,
the replacement field {.3f}, specifies fixed-point notation with a precision
of 3.
To include the literal character { in the formatted output, you can write
{{, and similarly for } and }}. For example, the following definition
array A = [3] U32 format "{{element {}}}"specifies a format string element {0} for element value 0.
No other use of { or } in a format string is allowed. For example, this is illegal:
array A = [3] U32 format "{" # Illegal use of { characterYou can include both a default value and a format; in this case, the default value must come first. For example:
array WheelSpeeds = [3] U32 default 100 format "{} RPM"If you don’t specify an element format, then each element is displayed
using the default format for its type.
Therefore, omitting the format string is equivalent to writing the format
string "{}".
6.1.5. Arrays of Arrays
An array type may have another array type as its element type. In this way you can construct an array of arrays. For example:
array A = [3] U32
array B = [3] A # An array of 3 A, which is an array of 3 U32When constructing an array of arrays, you may provide any legal default expression, so long as the types are compatible. For example:
array A = [2] U32 default 10 # default value is [ 10, 10 ]
array B1 = [2] A # default value is [ [ 10, 10 ], [ 10, 10 ] ]
array B2 = [2] A default 1 # default value is [ [ 1, 1 ], [ 1, 1 ] ]
array B3 = [2] A default [ 1, 2 ] # default value is [ [ 1, 1 ], [ 2, 2 ] ]
array B4 = [2] A default [ [ 1, 2 ], [ 3, 4 ] ]6.2. Struct Type Definitions
A struct type definition associates a name with a struct type. A struct type describes the shape of a struct value. It specifies a mapping from element names to their types. As discussed below, it also specifies a serialization order for the struct elements.
6.2.1. Writing a Struct Type Definition
As an example, here is a struct type definition that associates the name S with
a struct type containing two members: x of type U32, and y of type string:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct S { x: U32, y: string }In general, to write a struct type definition, you write the following:
-
The keyword
struct. -
The name of the struct type.
-
A sequence of struct type members enclosed in curly braces
{…}.
A struct type member consists of a name, a colon, and a
type name,
for example x: U32.
The struct type members form an element sequence in which the optional terminating punctuation is a comma. As usual for element sequences, you can omit the comma and use a newline instead. So, for example, we can write the definition shown above in this alternate way:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct S {
x: U32
y: string
}6.2.2. Annotating a Struct Type Definition
As noted in the beginning of this section, a type definition is an annotatable element, so you can attach pre and post annotations to it. A struct type member is also an annotatable element, so any struct type member can have pre and post annotations as well. Here is an example:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
@ This is a pre annotation for struct S
struct S {
@ This is a pre annotation for member x
x: U32 @< This is a post annotation for member x
@ This is a pre annotation for member y
y: string @< This is a post annotation for member y
} @< This is a post annotation for struct S6.2.3. Default Values
You can specify an optional default value for a struct definition.
To do this, you write the keyword default and an expression
that evaluates to a struct
value.
For example, here is a struct type S with default value { x = 1, y = "abc"
}:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct S { x: U32, y: string } default { x = 1, y = "abc" }A default value expression need not be a literal struct value; it can be any expression with the correct type. For example, you can create a named constant with a struct value and use it multiple times, like this:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
constant s = { x = 1, y = "abc" }
struct S1 { x: U8, y: string } default s
struct S2 { x: U32, y: string } default sIf you don’t specify a default value, then the struct type gets an automatic default value, consisting of the default value for each member.
The type of the default expression must match the type of the struct, with type conversions allowed as discussed for struct values. For example, this default expression is allowed, because we can convert integer values to floating-point values, and we can promote a single value to a struct with numeric members:
struct S { x: F32, y: F32 } default 1 # default value is { x = 1.0, y = 1.0 }And this default expression is allowed, because if we omit a member of a struct, then FPP will fill in the member and give it the default value:
struct S { x: F32, y: F32 } default { x = 1 } # default value is { x = 1.0, y = 0.0 }However, these default expressions are not allowed:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct S1 { x: U32, y: string } default { z = 1 } # Error: member z does not matchtype FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct S2 { x: U32, y: string } default { x = "abc" } # Error: type of member x does not match6.2.4. Member Arrays
For any struct member, you can specify that the member is an array of elements. To do this you, write an array the size enclosed in square brackets before the member type. For example:
struct S {
x: [3] U32
}This definition says that struct S has one element x,
which is an array consisting of three U32 values.
We call this array a member array.
Member arrays vs. array types: Member arrays let you include an array of elements as a member of a struct type, without defining a separate named array type. Also, member arrays generate less code than named arrays. Whereas a member size array is a native C++ array, each named array is a C++ class.
On the other hand, defining a named array is usually a good choice when
-
You want to use the array outside of any structure.
-
You want the convenience of a generated array class, which has a richer interface than the bare C++ array.
In particular, the generated array class provides bounds-checked access operations: it causes a runtime failure if an out-of-bounds access occurs. The bounds checking provides an additional degree of memory safety when accessing array elements.
Member arrays and default values: FPP ignores member array sizes when checking the types of default values. For example, this code is accepted:
struct S {
x: [3] U32
} default { x = 10 }The member x of the struct S gets three copies of the value
10 specified for x in the default value expression.
6.2.5. Member Format Strings
For any struct member, you can include an optional format.
To do this, write the keyword format and a format string.
The format string for a struct member has the same form as for an
array member.
For example, the following struct definition specifies
that member x should be displayed as a hexadecimal value:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct Channel {
name: string
offset: U32 format "offset 0x{x}"
}How the entire struct is displayed depends on the implementation.
As an example, the value of S with name = "momentum" and offset = 1024
might look like this when displayed:
Channel { name = "momentum", offset = 0x400 }
If you don’t specify a format for a struct member, then the system uses the default format for the type of that member.
If the member has a size greater than one, then the format is applied to each element. For example:
struct Telemetry {
velocity: [3] F32 format "{} m/s"
}The format string is applied to each of the three
elements of the member velocity.
6.2.6. Struct Types Containing Named Types
A struct type may have an array or struct type as a member type. In this way you can define a struct that has arrays or structs as members. For example:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
array Speeds = [3] U32
# Member speeds has type Speeds, which is an array of 3 U32 values
struct Wheel { name: string, speeds: Speeds }When initializing a struct, you may provide any legal default expression, so long as the types are compatible. For example:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
array A = [2] U32
struct S1 { x: U32, y: string }
# default value is { s1 = { x = 0, y = "" }, a = [ 0, 0 ] }
struct S2 { s1: S1, a: A }
# default value is { s1 = { x = 0, y = "abc" }, a = [ 5, 5 ] }
struct S3 { s1: S1, a: A } default { s1 = { y = "abc" }, a = 5 }6.2.7. The Order of Members
For struct values,
we said that the order in which the members appear in the value is not
significant.
For example, the expressions { x = 1, y = 2 } and { y = 2, x = 1 } denote
the same value.
For struct types, the rule is different.
The order in which the members appear is significant, because
it governs the order in which the members appear in the generated
code.
For example, the type struct S1 { x: U32, y : string } might generate a C++
class S1 with members x and y laid out with x first; while struct S2
{ y : string, x : U32 }
might generate a C++ class S2 with members x and y laid out with y
first.
Since class members are generally serialized in the order in which they appear in
the class,
the members of S1 would be serialized with x first, and the members of
S2
would be serialized with y first.
Serializing S1 to data and then trying to deserialize it to S2 would
produce garbage.
The order matters only for purposes of defining the type, not for assigning default values to it. For example, this code is legal:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
struct S { x: U32, y: string } default { y = "abc", x = 5 }FPP struct values have no inherent order associated with their members. However, once those values are assigned to a named struct type, the order becomes fixed.
6.3. Abstract Type Definitions
An array or struct type definition specifies a complete type: in addition to the name of the type, it provides the names and types of all the members. An abstract type, by contrast, has an incomplete or opaque definition. It provides only a name N. Its purpose is to tell the analyzer that a type with name N exists and will be defined elsewhere. For example, if the target language is C++, then the type is a C++ class.
To define an abstract type, you write the keyword type followed
by the name of the type.
For example, you can define an abstract type T; then you can construct
an array A with member type T:
type T # T is an abstract type
array A = [3] T # A is an array of 3 values of type TThis code says the following:
-
A type
Texists. It is defined in the implementation, but not in the model. -
Ais an array of three values, each of typeT.
Now suppose that the target language is C++. Then the following happens when generating code:
-
The definition
type Tdoes not cause any code to be generated. -
The definition
array A =… causes a C++ classAto be generated. By F Prime convention, the generated files areAArrayAc.hppandAArrayAc.cpp. -
File
AArrayAc.hppincludes a header fileT.hpp.
It is up to the user to implement a C++ class T with
a header file T.hpp.
This header file must define T in a way that is compatible
with the way that T is used in A.
We will have more to say about this topic in the section on
implementing abstract types.
In general, an abstract type T is opaque in the FPP model
and has no values that are expressible in the model.
Thus, every use of an abstract type T represents the default value
for T.
The implementation of T in the target language
provides the default value.
In particular, when the target language is C++, the default
value is the zero-argument constructor T().
6.4. Alias Type Definitions
An alias type definition provides an alternate name for
a type that is defined elsewhere.
The alternate name is called an alias of the original type.
For example, here is an alias type definition specifying that the type
T is an alias of the type U32:
type T = U32Wherever this definition is available, the type T may be used
interchangeably with the type U32.
For example:
type T = U32
array A = [3] TAn alias type definition may refer to any type, including another
alias type, except that it may not refer to itself, either directly or through
another alias.
For example, here is an alias type definition specifying that the type
T is an alias of the struct type S:
struct S { x: U32, y: I32 }
type T = SHere is a pair of definitions specifying that S is an alias of T,
and T is an alias of F32:
type S = T
type T = F32Here is a pair of alias type definitions that is illegal, because each of the definitions indirectly refers to itself:
type S = T
type T = SAlias type definitions are useful for specifying configurations.
Part of a model can use a type T, without
defining T; elsewhere, configuration code can define
T to be the alias of another type.
F Prime uses this method to provide basic type whose definitions
configure the framework.
These types are defined in the file config/FpConfig.fpp.
6.5. Framework Types
Certain types defined in FPP have a special meaning in the F Prime
framework.
These types are called framework types.
For example, the type FwOpcodeType defines the type of
a command opcode.
(Commands are an F Prime feature that we describe
in a later section of this manual.)
Framework types are like framework constants: you typically define them by overriding configuration files provided by F Prime, and if they are defined, then they must conform to certain rules. The FPP Language Specification has all the details.
7. Defining Enums
An FPP model may contain one or more enum definitions. Enum is short for enumeration. An FPP enum is similar to an enum in C or C++. It defines a named type called an enum type and a set of named constants called enumerated constants. The enumerated constants are the values associated with the type.
An enum definition may appear at the top level or inside a module definition. An enum definition is an annotatable element.
7.1. Writing an Enum Definition
Here is an example:
enum Decision {
YES
NO
MAYBE
}This code defines an enum type Decision with three
enumerated constants: YES, NO, and MAYBE.
In general, to write an enum definition, you write the following:
-
The keyword
enum. -
The name of the enum.
-
A sequence of enumerated constants enclosed in curly braces
{…}.
The enumerated constants form an element sequence in which the optional terminating punctuation is a comma. For example, this definition is equivalent to the one above:
enum Decision { YES, NO, MAYBE }There must be at least one enumerated constant.
7.2. Using an Enum Definition
Once you have defined an enum, you can use the enum as a type and the enumerated constants as constants of that type. The name of each enumerated constant is qualified by the enum name. Here is an example:
enum State { ON, OFF }
constant initialState = State.OFFThe constant s has type State and value State.ON.
Here is another example:
enum Decision { YES, NO, MAYBE }
array Decisions = [3] Decision default Decision.MAYBEHere we have used the enum type as the type of the array member,
and we have used the value Decision.MAYBE as the default
value of an array member.
7.3. Numeric Values
As in C and C++, each enumerated constant has an associated
numeric value.
By default, the values start at zero and go up by one.
For example, in the enum Decision defined above,
YES has value 0, NO has value 1, and MAYBE has value 2.
You can optionally assign explicit values to the enumerated constants. To do this, you write an equals sign and an expression after each of the constant definitions. Here is an example:
enum E { A = 1, B = 2, C = 3 }This definition creates an enum type E with three enumerated constants E.A,
E.B, and E.C. The constants have 1, 2, and 3 as their associated numeric
values.
If you provide an explicit numeric value for any of the enumerated constants, then you must do so for all of them. For example, this code is not allowed:
# Error: cannot provide a value for just one enumerated constant
enum E { A = 1, B, C }Further, the values must be distinct.
For example, this code is not allowed, because
the enumerated constants A and B both have the value 2:
# Error: enumerated constant values must be distinct
enum E { A = 2, B = 1 + 1 }You may convert an enumerated constant to its associated numeric value. For example, this code is allowed:
enum E { A = 5 }
constant c = E.A + 1The constant c has the value 6.
However, you may not convert a numeric value to an enumerated constant. This is for type safety reasons: a value of enumeration type should have one of the numeric values specified in the type. Assigning an arbitrary number to an enum type would violate this rule.
For example, this code is not allowed:
enum E { A, B, C }
# Error: cannot assign integer 10 to type E
array A = [3] E default 107.4. The Representation Type
Each enum definition has an associated representation type. This is the primitive integer type used to represent the numeric values associated with the enumerated constants when generating code.
If you don’t specify a representation type, then the default
type is I32.
For example, in the enumerations defined in the previous sections,
the representation type is I32.
To specify an explicit representation type, you write it after
the enum name, separated from the name by a colon, like this:
enum Small : U8 { A, B, C }This code defines an enum Small with three enumerated constants
Small.A, Small.B, and Small.C.
Each of the enumerated constants is represented as a U8 value
in C++.
7.5. The Default Value
Every type in FPP has an associated default value. For enum types, if you don’t specify a default value explicitly, then the default value is the first enumerated constant in the definition. For example, given this definition
enum Decision { YES, NO, MAYBE }the default value for the type Decision is Decision.YES.
That may be too permissive, say if Decision represents
a decision on a bank loan.
Perhaps the default value should be Decision.MAYBE.
To specify an explicit default value, write the keyword default
and the enumerated constant after the enumerated constant
definitions, like this:
enum Decision { YES, NO, MAYBE } default MAYBENotice that when using the constant MAYBE as a default value, we
don’t need to qualify it with the enum name, because the
use appears inside the enum where it is defined.
8. Dictionary Definitions
One of the artifacts generated from an FPP model is a dictionary that tells the ground data system how to interpret and display the data produced by the FSW. By default, the dictionary contains representations of the following types and constants defined in FPP:
-
Types and constants that are known to the framework and that are needed by every dictionary, e.g.,
FwOpcodeType. -
Types and constants that appear in the definitions of the data produced by the FSW, e.g., event specifiers or telemetry specifiers. (In later sections of this manual we will explain how to define event reports and telemetry channels.)
Sometimes you will need the dictionary to include the definition of a type or constant that does not satisfy either of these conditions. For example, a downlink configuration parameter may be shared by the FSW implementation and the GDS and may be otherwise unused in the FPP model.
In this case you can mark a type or constant definition as a dictionary definition. A dictionary definition tells the FPP analyzer that whenever a dictionary is generated from the model, the definition should be included in the dictionary.
To write a dictionary definition, you write the keyword dictionary
before the definition.
You can do this for a constant definition, a type definition,
or an enum definition.
For example:
dictionary constant a = 1
dictionary array A = [3] U32
dictionary struct S { x: U32, y: F32 }
dictionary type T = S
dictionary enum E { A, B }Each dictionary definition must observe the following rules:
-
A dictionary constant definition must have a numeric value (integer or floating point), a Boolean value (true or false), a string value such as
"abc", or an enumerated constant value such asE.A. -
A dictionary type definition must define a displayable type, i.e., a type that the F Prime ground data system knows how to display. For example, the type may not be an abstract type. Nor may it be an array or struct type that has an abstract type as a member type.
For example, the following dictionary definitions are invalid:
dictionary constant a = { x = 1, y = 2.0 } # Error: a has struct type
dictionary type T # Error: T is an abstract type9. Defining Ports
A port definition defines an F Prime port. In F Prime, a port specifies the endpoint of a connection between two component instances. Components are the basic units of FSW function in F Prime and are described in the next section. A port definition specifies (1) the name of the port, (2) the type of the data carried on the port, and (3) an optional return type.
9.1. Port Names
The simplest port definition consists of the keyword port followed
by a name.
For example:
port PThis code defines a port named P that carries no data and returns
no data.
This kind of port can be useful for sending or receiving a triggering event.
9.2. Formal Parameters
More often, a port will carry data. To specify the data, you write formal parameters enclosed in parentheses. The formal parameters of a port definition are similar to the formal parameters of a function in a programming language: each one has a name and a type, and you may write zero or more of them. For example:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
port P1() # Zero parameters; equivalent to port P1
port P2(a: U32) # One parameter
port P3(a: I32, b: F32, c: string) # Three parametersThe type of a formal parameter may be any valid type, including an
array type, a struct type, an enum type, or an abstract type.
For example, here is some code that defines an enum type E and
and abstract type T, and then uses those types in the
formal parameters of a port:
enum E { A, B }
type T
port P(e: E, t: T)The formal parameters form an element sequence in which the optional terminating punctuation is a comma. As usual for element sequences, you can omit the comma and use a newline instead. So, for example, we can write the definition shown above in this alternate way:
enum E { A, B }
type T
port P(
e: E
t: T
)9.3. Handler Functions
As discussed further in the sections on
defining components
and
instantiating components,
when constructing an F Prime application, you
instantiate port definitions as output ports and
input ports of component instances.
Output ports are connected to input ports.
For each output port pOut of a component instance c1,
there is a corresponding auto-generated function that the
implementation of c1 can call in order to invoke pOut.
If pOut is connected to an input
port pIn of component instance c2, then invoking pOut runs a
handler function pIn_handler associated with pIn.
The handler function is part of the implementation of the component
C2 that c2 instantiates.
In this way c1 can send data to c2 or request
that c2 take some action.
Each input port may be synchronous or asynchronous.
A synchronous invocation directly calls a handler function.
An asynchronous invocation calls a short function that puts
a message on a queue for later dispatch.
Dispatching the message calls the handler function.
Translating handler functions:
In FPP, each output port pOut or input port pIn has a port type.
This port type refers to an FPP port definition P.
In the C++ translation, the signature of a handler function
pIn_handler for pIn
is derived from P.
In particular, the C++ formal parameters of pIn_handler
correspond to the
FPP formal parameters of P.
When generating the handler function pIn_handler, F
Prime translates each formal parameter p of P in the following way:
-
If p carries a primitive value, then p is translated to a C++ value parameter.
-
Otherwise p is translated to a C++
constreference parameter.
As an example, suppose that P looks like this:
type T
port P(a: U32, b: T)Then the signature of pIn_handler might look like this:
virtual void pIn_handler(U32 a, const T& b);Calling handler functions:
Suppose again that output port pOut of component instance c1
is connected to input port pIn of component instance c2.
Suppose that the implementation of c1 invokes pOut.
What happens next depends on whether pIn is synchronous
or asynchronous.
If pIn is synchronous, then the invocation is a direct
call of the pIn handler function.
Any value parameter is passed by copying the value on
the stack.
Any const reference parameter provides a reference to
the data passed in by c1 at the point of invocation.
For example, if pIn has the port type P shown above,
then the implementation of pIn_handler might look like this:
// Assume pIn is a synchronous input port
void C2::pIn_handler(U32 a, const T& b) {
// a is a local copy of a U32 value
// b is a const reference to T data passed in by c1
}Usually the const reference is what you want, for efficiency reasons.
If you want a local copy of the data, you can make one.
For example:
// Copy b into b1
auto b1 = bNow b1 has the same data that the parameter b would have
if it were passed by value.
If pIn is asynchronous, then the invocation does not
call the handler directly. Instead, it calls
a function that puts a message on a queue.
The handler is called when the message is dispatched.
At this point, any value parameter is passed by
copying the value out of the queue and onto the stack.
Any const reference parameter is passed by
(1) copying data out of the queue and onto the stack and
(2) then providing a const reference to the data on the stack.
For example:
// Assume pIn is an asynchronous input port
void C2::pIn_handler(U32 a, const T& b) {
// a is a local copy of a U32 value
// b is a const reference to T data copied across the queue
// and owned by this component
}Note that unlike in the synchronous case, const references in parameters refer to data owned by the handler (residing on the handler stack), not data owned by the invoking component. Note also that the values must be small enough to permit placement on the queue and on the stack.
If you want the handler and the invoking component to share data
passed in as a parameter, or if the data values are too large
for the queue and the stack, then you can use a data structure
that contains a pointer or a reference as a member.
For example, T could have a member that stores a reference
or a pointer to shared data.
F Prime provides a type Fw::Buffer that stores a
pointer to a shared data buffer.
Passing string arguments:
Suppose that an input port pIn of a component instance c
has port type P.
If P has a formal parameter of type string,
the corresponding formal parameter in the handler for pIn is
a constant reference to Fw::StringBase, which is an abstract
supertype of all F Prime string types.
The string object referred to depends on whether pIn is synchronous
or asynchronous:
-
If
pInis synchronous, then the reference is to the string object used in the invocation. In this case the size specified in thestringtype is ignored. For example, if a string of length 80 is bound to a port parameter whose type isstring size 40, the reference is to the original string of length 80. -
If
pInis asynchronous, then the reference is to a string object on the stack whose size is bounded by the size named in the port parameter. For example, if a string of length 80 is bound to a port parameter whose type isstring size 40, then the reference is to a string consisting of the first 40 characters of the original string.
9.4. Reference Parameters
You may write the keyword ref in front of any formal parameter p
of a port definition.
Doing this specifies that p is a reference parameter.
Each reference parameter in an FPP port becomes a mutable
C++ reference at the corresponding place in the
handler function signature.
For example, suppose this port definition
type T
port P(a: U32, b: T, ref c: T)appears as the type of an input port pIn of component C.
The generated code for C might contain a handler function with a
signature like this:
virtual void pIn_handler(U32 a, const T& b, T& c);Notice that parameter b is not marked ref, so it is
translated to const T& b, as discussed in the previous section.
On the other hand, parameter c is marked ref, so it
is translated to T& c.
Apart from the mutability, a reference parameter has the same
behavior as a const reference parameter, as described in
the previous section.
In particular:
-
When
pInis synchronous, a reference parameter p ofpIn_handlerrefers to the data passed in by the invoking component. -
When
pInis asynchronous, a reference parameter p ofpIn_handlerrefers to data copied out of the queue and placed on the local stack.
The main reason to use a reference parameter is to return a value to the sender by storing it through the reference. We discuss this pattern in the section on returning values.
9.5. Returning Values
Optionally, you can give a port definition a return type.
To do this you write an arrow -> and a type
after the name and the formal parameters, if any.
For example:
type T
port P1 -> U32 # No parameters, returns U32
port P2(a: U32, b: F32) -> T # Two parameters, returns TInvoking a port with a return type is like calling a function with a return value. Such a port may be used only in a synchronous context (i.e., as a direct function call, not as a message placed on a concurrent queue).
In a synchronous context only, ref parameters provide another way to return
values on the port,
by assigning to the reference, instead of executing a C++ return statement.
As an example, consider the following two port definitions:
type T
port P1 -> T
port P2(ref t: T)The similarities and differences are as follows:
-
Both
P1andP2must be used in a synchronous context, because each returns aTvalue. -
In the generated C++ code,
-
The function for invoking
P1has no arguments and returns aTvalue. A handler associated withP1returns a value of typeTvia the C++returnstatement. For example:T C::p1In_handler() { ... return T(1, 2, 3); } -
The function for invoking
P1has one argumenttof typeT&. A handler associated withP2returns a value of typeTby updating the referencet(assigning to it, or updating its fields). For example:void C::p2In_handler(T& t) { ... t = T(1, 2, 3); }
-
The second way may involve less copying of data.
Finally, there can be any number of reference parameters,
but at most one return value.
So if you need to return multiple values on a port, then reference
parameters can be useful.
As an example, the following port attempts to update a result
value of type U32.
It does this via reference parameter.
It also returns a status value indicating whether the update
was successful.
enum Status { SUCCEED, FAIL }
port P(ref result: U32) -> StatusA handler for P might look like this:
Status C::pIn_handler(U32& result) {
Status status = Status::FAIL;
if (...) {
...
result = ...
status = Status::SUCCEED;
}
return status;
}
9.6. Pass-by-Reference Semantics
Whenever a C++ formal parameter p enables sharing of data between
an invoking component and a handler function pIn_handler,
we say that p has pass-by-reference semantics.
Pass-by-reference semantics occurs in the following cases:
-
p has reference or
constreference type, and the portpInis synchronous. -
p has a type T that contains a pointer or a reference as a member.
When using pass-by-reference semantics, you must carefully manage the use of the data to avoid concurrency bugs such as data races. This is especially true for references that can modify shared data.
Except in special cases that require special expertise (e.g.,
the implementation of highly concurrent data structures),
you should enforce the rule that at most
one component may use any piece of data at any time.
In particular, if component A passes a reference to component B,
then component A should not use the reference while
component B is using it, and vice versa.
For example:
-
Suppose component
Aowns some dataDand passes a reference toDvia a synchronous port call to componentB. Suppose the port handler in componentBuses the data but does not store the reference, so that when the handler exits, the reference is lost. This is a good pattern. In this case, we may say that ownership ofDresides inA, temporarily goes toBfor the life of the handler, and goes back toAwhen the handler exits. Because the port call is synchronous, the handler inBnever runs concurrently with any code inAthat usesD. So at most one ofAorBusesDat any time. -
Suppose instead that the handler in
Bstores the reference into a member variable, so that the reference persists after the handler exits. If this happens, then you should make sure thatAcannot useDunless and untilBpasses ownership ofDtoAand vice versa. For example, you could use state variables of enum type inAand inBto track ownership, and you could have a port invocation fromAtoBpass the reference and transfer ownership fromAtoBand vice versa.
9.7. Annotating a Port Definition
A port definition is an annotatable element. Each formal parameter is also an annotatable element. Here is an example:
@ Pre annotation for port P
port P(
@ Pre annotation for parameter a
a: U32
@ Pre annotation for parameter b
b: F32
)10. Defining State Machines
A hierarchical state machine (state machine for short) is a software subsystem that specifies the following:
-
A set of states that the system can be in. The states can be arranged in a hierarchy (i.e., states may have substates).
-
A set of transitions from one state to another that occur under specified conditions.
State machines are important in embedded programming. For example, F Prime components often have a concept of state that changes as the system runs, and it is useful to model these state changes as a state machine.
In FPP there are two ways to define a state machine:
-
An external state machine definition is like an abstract type definition: it tells the analyzer that a state machine exists with a specified name, but it says nothing about the state machine behavior. An external tool must provide the state machine implementation.
-
An internal state machine definition is like an array type definition or struct type definition: it provides a complete specification in FPP of the state machine behavior. The FPP back end uses this specification to generate code; no external tool is required.
The following subsections describe both kinds of state machine definitions.
State machine definitions may appear at the top level or inside a module definition. A state machine definition is an annotatable element. Once you define a state machine, you can instantiate it as part of a component. The component can then send the signals that cause the state transitions. The component also provides the functions that are called when the state machine does actions and evaluates guards.
10.1. Writing a State Machine Definition
External state machines:
To define an external state machine, you write the keywords
state machine followed by an identifier, which is the
name of the state machine:
state machine MThis code defines an external state machine with name M.
When you define an external state machine M, you must provide
an implementation for M, as discussed in the section
on implementing external state machines.
The external implementation must have a header file M.hpp
located in the same directory as the FPP file where
the state machine M is defined.
Internal state machines: In the following subsections, we explain how to define internal state machines in FPP. The behavior of these state machines closely follows the behavior described for state machines in the Universal Modeling Language (UML). UML is a graphical language and FPP is a textual language, but each of the concepts in the FPP language is motivated by a corresponding UML concept. FPP does not represent every aspect of UML state machines: because our goal is to support embedded and flight software, we focus on a subset of UML state machine behavior that is (1) simple and unambiguous and (2) sufficient for embedded applications that use F Prime.
In this manual, we focus on the syntax and high-level behavior of FPP state machines. For more details about the C++ code generation for state machines, see the F Prime design documentation.
10.2. States, Signals, and Transitions
In this and the following sections, we explain how to define internal state machines, i.e., state machines that are fully specified in FPP. In these sections, when we say “state machine,” we mean an internal state machine.
First we explain the concepts of states, signals, and transitions. These are the basic building blocks of FPP state machines.
Basic state machines: The simplest state machine M that has any useful behavior consists of the following:
-
Several state definitions. These define the states of M.
-
An initial transition specifier. This specifies the state that an instance of M is in when it starts up.
-
One or more signal definitions. The external environment (typically an F Prime component) sends signals to instances of M.
-
One or more state transition specifiers. These tell each instance of M what to do when it receives a signal.
Here is an example:
@ A state machine representing a device with on-off behavior
state machine Device {
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
on cmdOn enter ON
}
}Here is the example represented graphically, as a UML state machine:
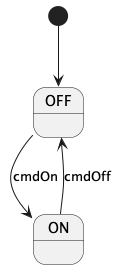
This example defines a state machine Device that represents
a device with on-off behavior.
There are two states, ON and OFF.
The initial transition specifier initial enter OFF
says that the state machine is in state OFF when it starts up.
There are two signals: cmdOn for turning the device
on and cmdOff for turning the device off.
There are two state transition specifiers:
-
A specifier that says to enter state
OFFon receiving thecmdOffsignal in stateON. -
A specifier that says to enter state
ONon receiving thecmdOnsignal in stateOFF.
In general, a state transition specifier causes a transition
from the state S in which it appears to the state S' that
appears after the keyword enter.
We say that S is the source of the transition,
and S' is the target of the transition.
If a state machine instance receives a signal s, and it is
in a state S that specifies no behavior for signal s
(i.e., there is no transition with source S and signal s),
then nothing happens.
In the example above, if the state machine receives signal
cmdOn in state ON
or signal cmdOff in state OFF, then it takes no action.
Rules for defining state machines: Each state machine definition must conform to the following rules:
-
A state machine definition and each of its members is an annotatable element. For example, you can annotate the
Devicestate machine as shown above. The members of a state machine definition form an element sequence with a semicolon as the optional terminating punctuation. The same rules apply to the members of a state definition. -
Each state machine definition must have exactly one initial transition specifier that names a state of the state machine. For example, if we deleted the initial transition specifier from the example above and passed the result through
fpp-check, an error would occur. -
Every state definition must be reachable from the initial transition specifier or from a state transition specifier. For example, if we deleted the state transition specifier in the state
ONfrom the example above and passed the result throughfpp-check, an error would occur. In this case, there would be no way to reach theONstate. -
Every state name must be unique, and every signal name must be unique.
-
Each state may have at most one state transition specifier for each signal s. For example, if we added another transition to state
ONon signalcmdOff, the FPP analyzer would report an error.
Simple state definitions:
If a state definition has no transitions, then you can omit
the braces.
For example, here is a revised version of the Device state
machine that has an off-on transition but no on-off transition:
@ A state machine representing a device with on-only behavior
state machine Device {
@ A signal for turning the device on
signal cmdOn
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
on cmdOn enter ON
}
}Notice that state ON has a simple definition with no curly braces.
10.3. Actions
An action is a function that a state machine calls at a specified point in its behavior. In the FPP model, actions are abstract; in the C++ back end they become pure virtual functions that you implement. When a state machine instance calls the function associated with an action A, we say that it does A.
10.3.1. Actions in Transitions
To define an action, you write the keyword action followed
by the name of the action.
As with signals,
every action name must be unique.
To do an action, you write the keyword do
followed by a list of action names enclosed in curly braces.
You can do this in an initial transition specifier or in a
state transition specifier.
As an example, here is the Device state machine from the
previous section, with actions added:
@ A state machine representing a device with on-off behavior,
@ with actions on transitions
state machine Device {
@ Initial action 1
action initialAction1
@ Initial action 2
action initialAction2
@ An action on the transition from OFF to ON
action offOnAction
@ An action on the transition from ON to OFF
action onOffAction
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ The initial state is OFF
@ Before entering the initial state, do initialAction1 and then initialAction2
initial do { initialAction1, initialAction2 } enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
@ Before entering the OFF state, do onOffAction
on cmdOff do { onOffAction } enter OFF
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
@ Before entering the ON state, do offOnAction
on cmdOn do { offOnAction } enter ON
}
}Here is the graphical representation:
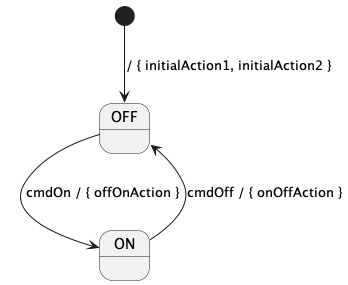
In this example there are four actions:
initialAction1, initialAction2, offOnAction, and onOffAction.
The behavior of each of these actions is specified in the C++
implementation; for example, each could emit an
F Prime event.
The state machine has the following behavior:
-
On startup, do
initialAction1, doinitialAction2, and enter theOFFstate. -
In state
OFF, on receiving thecmdOnsignal, dooffOnActionand enter theONstate. -
In state
ON, on receiving thecmdOffsignal, doonOffActionand enter theOFFstate.
When multiple actions appear in an action list, as in the initial transition specifier shown above, the actions occur in the order listed. Each action list is an element sequence with a comma as the optional terminating punctuation.
10.3.2. Entry and Exit Actions
In addition to doing actions on transitions, a state machine
can do actions on entry to or exit from a state.
To do actions like this, you write state entry specifiers
and state exit specifiers.
For example, here is the Device state machine from
the previous section, with state entry and exit specifiers
added to the ON and OFF states:
@ A state machine representing a device with on-off behavior,
@ with actions on transitions and on state entry and exit
state machine Device {
@ Initial action 1
action initialAction1
@ Initial action 2
action initialAction2
@ An action on the transition from OFF to ON
action offOnAction
@ An action on the transition from ON to OFF
action onOffAction
@ An action on entering the ON state
action enterOn
@ An action on exiting the ON state
action exitOn
@ An action on entering the OFF state
action enterOff
@ An action on exiting the OFF state
action exitOff
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ The initial state is OFF
@ Before entering the initial state, do initialAction1 and then initialAction2
initial do { initialAction1, initialAction2 } enter OFF
@ The ON state
state ON {
@ On entering the ON state, do enterOn
entry do { enterOn }
@ In the ON state, a cmdOff signal causes a transition to the OFF state
@ Before entering the OFF state, do offAction
on cmdOff do { onOffAction } enter OFF
@ On exiting the ON state, do exitOn
exit do { exitOn }
}
@ The OFF state
state OFF {
@ On entering the OFF state, do enterOff
entry do { enterOff }
@ In the OFF state, a cmdOff signal causes a transition to the ON state
@ Before entering the ON state, do onAction
on cmdOn do { offOnAction } enter ON
@ On exiting the OFF state, do exitOff
exit do { exitOff }
}
}Here is the graphical representation:
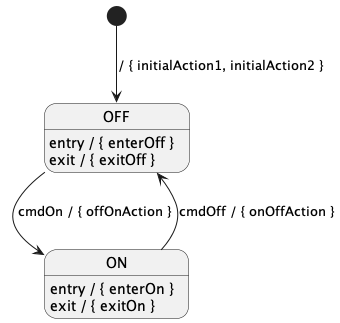
As with actions on transitions, each entry or exit specifier names
a list of actions, and the actions are done in the order named.
The entry actions are done just before entering the state,
and the exit actions are done just before exiting the state.
For example, if the state machine is in state OFF and it
receives a cmdOn signal, then it runs the following behavior,
in the following order:
-
Exit state
OFF. On exit, doexitOff. -
Transition from
OFFtoON. On the transition, dooffOnAction. -
Enter state
ON. On entry, doenterOn.
Each state may have at most one entry specifier and at most one exit specifier.
10.3.3. Typed Signals and Actions
Optionally, signals and actions may carry data values.
To specify that a signal or action carries a data value,
you write a colon and a data type at the end of the
signal or action specifier.
For example, here is a Device state machine in which
the cmdOn signal and the offOnAction each carries
a U32 counter value:
@ A state machine representing a device with on-off behavior,
@ with actions on transitions
state machine Device {
@ An action on the transition from OFF to ON
@ The value counts the number of times this action has occurred
action offOnAction: U32
@ A signal for turning the device on
@ The value counts the number of times this signal has been received
signal cmdOn: U32
@ A signal for turning the device off
signal cmdOff
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
@ Before entering the ON state, do offOnAction, passing the data from
@ the signal into the action
on cmdOn do { offOnAction } enter ON
}
}When you send the cmdOn signal to an instance of
this state machine, you must provide a U32 value.
When the state machine is in the OFF state and it receives
this signal, it does action offOnAction as shown.
The function that defines the behavior of offOnAction has
a single argument of type U32.
The value provided when the signal is sent is passed as the
argument to this function.
Here are the rules for writing typed signals and actions:
-
When you do an action that has a type, a value compatible with that type must be available. For example, we can’t do the
offOnActionin thecmdOfftransition shown above, because noU32value is available there. Similarly, no action done in a state entry or exit specifier may carry a value, because no values are available on entry to or exit from a state. -
The type that appears in a signal or an action can be any FPP type. In the example above we used a simple
U32type; we could have used, for example, a struct or array type. In particular, you can use a struct type to send several data values, with each value represented as a member of the struct. -
When doing an action with a value, you don’t have to make the types exactly match. For example, you are permitted to pass a
U16value to an action that requires aU32value. However, the type of the value must be convertible to the type specified in the action. The type conversion rules are spelled out in full in The FPP Language Specification. In general, the analyzer will allow a conversion if it can be safely done for all values of the original type. -
If an action A does not carry any value, then you can do A in any context, even if a value is available there. For example, in the code shown above, the
cmdOntransition could do some other action that carries no value. In this case the value is ignored when doing the action.
10.3.4. Atomicity of Signal Handling
When an FPP state machine receives a signal, the handling of that signal is atomic. That means that signals may be received concurrently, but they are handled one by one. For example, this sequence of events cannot occur:
-
In state S1, signal s1 is handled, causing an action A and a transition to state S2.
-
After doing action A, but before entering state S2, a signal s2 is handled.
Instead, s2 will be handled either before the handling of s1 starts or after the handling of s1 is complete. This atomicity guarantee is achieved by putting the signals on an input queue and using the queue to serialize the signal handler functions.
Because of the atomicity guarantee, the C++ implementation of an FPP state machine can safely send a signal s as part of its implementation for an action A. The action A will be run during the handling of a signal s'. When s' is handled and A is run, s is placed on the queue. After s' is complete, s is dispatched from the queue and handled.
For more details on sending signals to an FPP state machine, see the F Prime design documentation.
10.4. More on State Transitions
In this section, we provide more details on how to write state transitions in FPP state machines.
10.4.1. Guarded Transitions
Sometimes it is useful to specify that a transition should occur only if a certain condition is true. For example, you may want to turn on a device, but only if it is safe to do so. We call this kind of transition a guarded transition. To specify this transition, you define a guard, which is an abstract function that returns a Boolean value. Then you use the guard in a transition. Here is an example:
@ A device state machine with a guarded transition
state machine Device {
@ A guard for checking whether the device is in a safe state for power-on
guard powerOnIsSafe
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
@ if powerOnIsSafe evaluates to true. Otherwise no transition occurs.
on cmdOn if powerOnIsSafe enter ON
}
}Here is the graphical representation:
In this example, there is one guard, powerOnIsSafe.
The implementation of this function will return true
if it is safe to power on the device; otherwise it will
return false.
In state OFF, the transition on signal cmdOn is
now guarded: when the signal is received in this state,
the transition occurs if and only if powerOnIsSafe
evaluates to true.
As with actions, each guard must have a unique name.
Also as with actions, a guard can have a type; if it does,
the type must match the type of the signal at the point
where the guard is evaluated.
For example, here is a revised version of the previous
state machine that adds a value of type DeviceStatus
to the guard powerOnIsSafe:
@ A type representing the status of a device
type DeviceStatus
@ A device state machine with a guarded transition
state machine Device {
@ A guard for checking whether the device is in a safe state for power-on
@ The DeviceStatus value provides the current device status
guard powerOnIsSafe: DeviceStatus
@ A signal for turning the device on
@ The DeviceStatus value provides the current device status
signal cmdOn: DeviceStatus
@ A signal for turning the device off
signal cmdOff
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
@ if powerOnIsSafe evaluates to true. Otherwise no transition occurs.
on cmdOn if powerOnIsSafe enter ON
}
}When you send the signal cmdOn to an instance of this state
machine, you must provide a value of type DeviceStatus.
When the state machine instance evaluates the guard powerOnIsSafe,
it passes in the value as an argument to the function.
10.4.2. Self Transitions
When a state transition has the same state S as its source and its target, and S has no substates, we call the transition a self transition. In this case the following behavior occurs:
-
The state machine does the exit actions for S, if any.
-
The state machine does the actions specified in the transition, if any.
-
The state machine does the entry actions for S, if any.
Note that on a self transition, the state machine exits and reenters S. This behavior is a special case of a more general behavior that we will discuss below in connection with state hierarchy. Below we will also generalize the concept of a self transition to the case of a state with substates.
As an example, consider the following state machine:
@ A state machine representing a device with on-off behavior,
@ with a self transition
state machine Device {
@ An action on entering the ON state
action enterOn
@ An action to perform on reset
action reset
@ An action on exiting the ON state
action exitOn
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ A signal for resetting the device
signal cmdReset
@ The initial state is OFF
@ Before entering the initial state, do initialAction1 and then initialAction2
initial enter OFF
@ The ON state
state ON {
@ On entering the ON state, do enterOn
entry do { enterOn }
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
@ In the ON state, a cmdReset signal causes a self transition
on cmdReset do { reset } enter ON
@ On exiting the ON state, do exitOn
exit do { exitOn }
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
on cmdOn enter ON
}
}Here is the graphical representation:
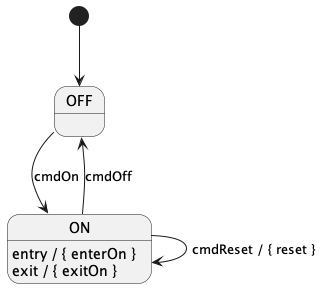
In this example, when the state machine is in the ON state and
it receives a cmdReset signal, the following behavior occurs:
-
Do action
exitOn. -
Do action
reset. -
Do action
enterOn.
10.4.3. Internal Transitions
An internal transition is like a
self transition,
except that there is no exit and reentry.
To write an internal transition, you write the on and do
parts of a transition and omit the enter part.
For example, here is a device state machine with a reset
action that causes an internal transition:
@ A state machine representing a device with on-off behavior,
@ with an internal transition
state machine Device {
@ An action on entering the ON state
action enterOn
@ An action to perform on reset
action reset
@ An action on exiting the ON state
action exitOn
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ A signal for resetting the device
signal cmdReset
@ The initial state is OFF
@ Before entering the initial state, do initialAction1 and then initialAction2
initial enter OFF
@ The ON state
state ON {
@ On entering the ON state, do enterOn
entry do { enterOn }
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
@ In the ON state, a cmdReset signal causes an internal transition
on cmdReset do { reset }
@ On exiting the ON state, do exitOn
exit do { exitOn }
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the ON state
on cmdOn enter ON
}
}Here is the graphical representation:
In this example, when the state machine is in state ON and it
receives a cmdReset signal, it does the reset action and
performs no other behavior.
An internal transition may have a guard.
For example, we could define a guard resetIsSafe and
write the internal transition as follows:
on cmdReset if resetIsSafe do { reset }As with other transitions, if the signal carries data, then any actions and guards named in an internal transition may carry data of a compatible type.
10.5. Choices
A choice definition is a state machine member that defines a branch point for one or more transitions. In this section we explain how to write and use choice definitions.
Basic choice definitions: The most basic choice definition consists of the following:
-
A name. Like a state name, this name can be the target of a transition.
-
The name of a guard G. The evaluation of G selects which branch of the choice to follow.
-
An if transition that specifies what to do if G evaluates to
true. -
An else transition that specifies what to do if G evaluates to
false.
Each of the if and else transitions has a target, which can be a state or a choice.
Here is an example:
@ A device state machine with a choice
state machine Device {
@ A guard for checking whether the device is in a safe state for power-on
guard powerOnIsSafe
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ A signal for resetting the device
signal cmdReset
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
}
@ The OFF state
state OFF {
@ In the OFF state, a cmdOff signal causes a transition to the choice ON_OR_ERROR
on cmdOn enter ON_OR_ERROR
}
@ The ON_OR_ERROR choice
choice ON_OR_ERROR {
if powerOnIsSafe enter ON else enter ERROR
}
@ The ERROR state
state ERROR {
@ In the ERROR state, a cmdReset signal causes a transition to the OFF state
on cmdReset enter OFF
}
}Here is the graphical representation:
This version of the Device state machine has three states:
ON, OFF, and ERROR.
It also has a choice ON_OR_ERROR.
Each instance of the state machine has the following behavior:
-
The initial state is
OFF. -
On receiving the signal
cmdOnin theOFFstate, it enters the choiceON_OR_ERROR. At that point, ifpowerOnIsSafeevaluates totrue, then it enters thenONstate. Otherwise it enters theERRORstate. -
On receiving the signal
cmdResetin theERRORstate, it enters theOFFstate. -
On receiving the signal
cmdOffin theONstate, it enters theOFFstate.
The text inside the curly braces of a choice consists of a single line. To write the text on multiple lines, you can use an explicit line continuation. For example:
choice ON_OR_ERROR {
if powerOnIsSafe \
enter ON \
else enter ERROR
}Initial transitions to choices:
An initial transition can go to a choice.
This pattern can express conditional behavior on state
machine startup.
For example, in the Device state machine shown above,
we could have the initial transition go to a choice
that checks a safety condition and then enters either
the OFF state or an error state.
Choice transitions to choices: An if transition or an else transition of a choice (or both) can enter another choice. For example, it is permissible to write a chain of choices like this:
choice C {
if g1 enter C1 else enter C2
}
choice C1 {
if g2 enter S1 else enter S2
}
choice C2 {
if g3 enter S3 else enter S4
}Effectively this is a four-way choice; it is a two-way
choice, each branch of which leads to a two way choice.
By having the if or else branch of C1 go directly
to a state, you could get a three-way choice.
And by adding more levels, you can create an n -way
choice for any n.
In this way you can use choices to create arbitrarily
complex branching patterns.
Note though, that it is usually a good idea not to have
more than a few levels of choices; otherwise the state
machine can be complex and hard to understand.
The type associated with a choice: Like initial transitions and state transitions, the transitions out of a choice may carry a value. To determine whether the transitions of a choice C carry a value, and if so what type that value has, we use the following rules:
-
If any transition into C carries no value, then transitions out of C carry no value.
-
Otherwise if all of the transitions into C carry a value of the same type T, then each of the transitions out of C carries a value of type T.
-
Otherwise if the incoming types can be resolved to a common type T, then each of the transitions out of C carries a value of type T. The rules for resolving common types are given in The FPP Language Specification. The basic idea is to find a type to which it is always safe to cast all the incoming types.
-
Otherwise the analyzer reports an error.
Actions in choice transitions:
You can do actions in choice transitions just as for
initial transitions and
state transitions.
For example, suppose we add the definitions of actions onAction and
errorAction to the Device state machine shown above.
Then we could revise the ON_OR_ERROR choice to read as follows:
choice ON_OR_ERROR {
if powerOnIsSafe do onAction enter ON else do errorAction enter ERROR
}As for other kinds of transitions, the actions done in choice transitions may carry values. If an action A done in a transition of a choice C carries a value, the type named in the definition of A must be compatible with the type associated with C, as discussed above.
Entry and exit actions: When a transition T of a state machine M goes to or from a choice, entry and exit actions are done as if each choice were a state with no entry and or exit actions. For example, let I be an instance of M, and suppose I is carrying out a transition T.
-
If T goes from a choice C to a state S, then I does the actions of T followed by the entry actions of S.
-
If T goes from a state S to a choice C, then I does the exit actions of S followed by the actions of T.
-
If T goes from a choice C1 to a choice C2, then I does the actions of T.
Rules for choice definitions: Choice definitions must conform to the following rules:
-
No state or choice may have the same name as any other state or choice.
-
Every choice must be reachable from the initial transition or from a state transition.
-
There may be no cycles of choice transitions. For example, it is not permitted for a choice
C1to have a transition to a choiceC2that has a transition back toC1. Nor is it permissible forC1to go toC2,C2to go toC3, andC3to go toC1.
10.6. Hierarchy
As with UML state machines, FPP state machines can have hierarchy. That is, we can do the following:
-
Define states within other states. When a state T is defined within a state S, S is called the parent of T, and T is called a substate or child of S.
-
Define choices within states.
Using hierarchy, we can do the following:
-
Group related substates under a single parent. This grouping lets us express the state machine structure in a disciplined and modular way.
-
Define behaviors of a parent state that are inherited by its substates. The parent behavior saves having to redefine the behavior for each substate.
-
Control the way that entry and exit actions occur when transitions cross state boundaries.
A state machine with hierarchy is called a hierarchical state machine. In the following subsections, we explain how to define hierarchical state machines in FPP.
10.6.1. Substates
In this section we explain how to define and use substates.
An example: Here is an example of a state machine with substates:
@ A device state machine with substates
state machine Device {
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ A signal for indicating that the device is in an unsafe state
signal cmdUnsafe
@ A signal for indicating that the device is in a safe state
signal cmdSafe
@ The initial state is OFF
initial enter OFF
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
@ In the ON state, a cmdUnsafe signal causes a transition to OFF.UNSAFE
on cmdUnsafe enter OFF.UNSAFE
}
@ The OFF state
state OFF {
@ The initial state is SAFE
initial enter SAFE
@ The state OFF.SAFE
@ In this state, it is safe to turn on the device
state SAFE {
@ In the SAFE state, a cmdOff signal causes a transition to the ON state
on cmdOn enter ON
@ In the SAFE state, a cmdUnsafe signal causes a transition to the UNSAFE state
on cmdUnsafe enter UNSAFE
}
@ The state OFF.UNSAFE
@ In this state, it is not safe to turn on the device
state UNSAFE {
@ In the UNSAFE state, a cmdSafe signal causes a transition to the SAFE state
on cmdSafe enter SAFE
}
}
}Here is the graphical representation:
This state machine has four states: ON, OFF, OFF.SAFE, and OFF.UNSAFE.
The last two states are substates of OFF.
Notice the following:
-
The substates are defined syntactically within the parent state.
-
The full names of the substates are qualified by the name of the parent state.
-
Inside the scope of the parent state, you can refer to the substates by the shorter name that omits the implied qualifier. The way the qualification works for state names is identical to the way it works for module names.
An instance m of this state machine has the following behavior:
-
When m starts up, it runs its initial transition specifier, just as for a state machine without hierarchy. The state machine enters state
OFF.OFFis a parent state, so it in turn has an initial transition specifier which is run. The state machine entersOFF.SAFE. -
In state
ON, the following behavior occurs:-
When m receives signal
cmdOff, it enters stateOFF. This entry causes it to enter stateOFF.SAFEas discussed above. -
When m receives signal
cmdUnsafe, it goes directly toOFF.UNSAFE, bypassing theOFFstate and its initial transition.
-
-
In state
OFF.SAFE, the following behavior occurs:-
When m receives signal
cmdOn, it enters theONstate. -
When m receives signal
cmdUnsafe, it enters theOFF.UNSAFEstate.
-
-
In state
OFF.UNSAFE, when m receives signalcmdSafe, it enters theOFF.SAFEstate.
Rules for substates: Here are the rules for defining substates:
-
Each parent state S must have exactly one initial transition specifier that enters a substate of S.
-
Each state, including parents and substates, must be reachable from the initial transition of the state machine or from a state transition.
-
Substates may themselves be parents (i.e., may have substates), to any depth.
Rule 1 ensures that the final target of every transition, after following all initial transition specifiers, is a leaf state, i.e., a state that has no substates.
The hierarchy tree: When a state S is a parent of a state S', we say that S is an ancestor of S' in the state hierarchy. We also say that S is an ancestor of S' if it is a parent of an ancestor of S'. For example, if S is a parent of a parent of S', then S is an ancestor of S'. Note that a state is never an ancestor of itself.
When a state S is a an ancestor of a state S', we say that S' is a descendant of S. For example, S' is a descendant of S if S' is a child of S, or if S' is a child of a child of S. Note that a state is never a descendant of itself.
In order to make the state hierarchy into a tree, we also say that the entire state machine M is a parent of every top-level state in the state machine. This means that (1) M is an ancestor of every state in M and (2) every state in M is a descendant of M. We will say that the tree constructed in this way is the hierarchy tree for M, and that each of M and every state in M is a node in the hierarchy tree. In particular, M is the root node of the hierarchy tree.
10.6.2. Inherited Transitions
In general, when a transition T is defined in a parent state S, T behaves as if it were defined in each of the leaf states that is a descendant of T. In this case we say that T is inherited by each of the leaf states. There is an important exception to this rule: When a state S defines a transition T on a signal s, and a descendant S' of S defines another transition T' on the same signal s, the behavior of T' takes precedence over the inherited transition T in the behavior of S'. This rule is called behavioral polymorphism for transitions.
Example: Here is an example that illustrates inherited transitions and behavioral polymorphism:
@ A device state machine with inherited transitions and behavioral polymorphism
state machine Device {
@ A signal for turning the device on
signal cmdOn
@ A signal for turning the device off
signal cmdOff
@ A signal for indicating that the device is in an unsafe state
signal cmdUnsafe
@ A signal for indicating that the device is in a safe state
signal cmdSafe
@ The initial state is DEVICE
initial enter DEVICE
@ The DEVICE state
state DEVICE {
@ The initial state is OFF
initial enter OFF
@ In the DEVICE state, a cmdUnsafe signal causes a transition to OFF.UNSAFE
on cmdUnsafe enter OFF.UNSAFE
@ The ON state
state ON {
@ In the ON state, a cmdOff signal causes a transition to the OFF state
on cmdOff enter OFF
}
@ The OFF state
state OFF {
@ The initial state is SAFE
initial enter SAFE
@ The state OFF.SAFE
@ In this state, it is safe to turn on the device
state SAFE {
@ In the SAFE state, a cmdOff signal causes a transition to the ON state
on cmdOn enter ON
}
@ The state OFF.UNSAFE
@ In this state, it is not safe to turn on the device
state UNSAFE {
@ In the UNSAFE state, a cmdSafe signal causes a transition to the SAFE state
on cmdSafe enter SAFE
@ In the UNSAFE state, a cmdUnsafe signal causes no action
on cmdUnsafe do { }
}
}
}
}Here is the graphical representation:
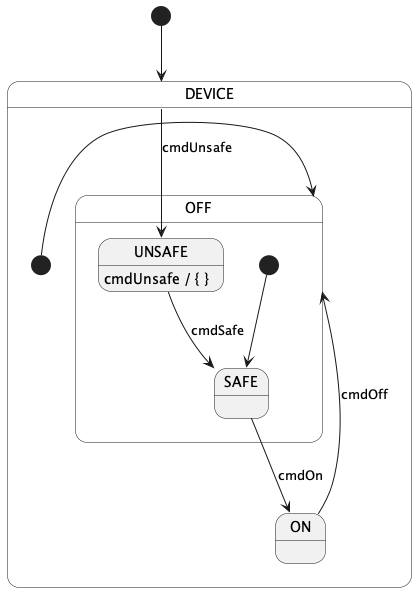
Here we have rewritten the
Device state machine from the previous section
so that all the states in that example are descendants of a single state
DEVICE.
By doing this, we can have a single transition out of DEVICE on signal
cmdUnsafe.
Before we had to write out the same transition twice,
once in the state ON and once in the state OFF.SAFE.
Here we can write the transition once in the ancestor state, and
it is inherited by all the descendants.
There is one catch, though: in the previous example, we did not define
the transition on cmdUnsafe in the state OFF.UNSAFE.
Here, if we use inheritance in the obvious way, the transition will
be inherited by all the descendants of DEVICE, including OFF.UNSAFE,
so the behavior will not be exactly the same as for the previous
state machine.
This may not matter much in this example, but it would matter if the
the state DEVICE.OFF.UNSAFE had entry or exit actions; in this case
transition from UNSAFE to itself (which is a
self transition)
would cause an exit from and reentry to the state, which we may not want.
To remedy this situation, we use behavioral polymorphism.
In the state DEVICE.OFF.UNSAFE, we define an
internal
transition
that has an empty list of actions and so does nothing.
This transition overrides the transition provided in the ancestor state,
so it restores the behavior that, on receipt of the signal
cmdUnsafe in the state DEVICE.OFF.UNSAFE, nothing happens.
Syntactic and flattened state transitions: Once we introduce substates and inheritance, it is useful to distinguish syntactic state transitions from flattened state transitions. A syntactic state transition is a state transition in the FPP source for a state machine M. A flattened state transition is a transition that results from applying the rules for transition inheritance to a syntactic state transition. We say the transition is “flattened” because we create it by moving the left side of the transition down to a leaf state. This move flattens the hierarchy on the left side of the transition.
When there is no hierarchy, a syntactic transition from state S1 to S2 generates exactly one flattened transition, also from S1 to S2. Once we have hierarchy, however, syntactic and flattened state transitions may be different. For example, suppose that S1 is a parent state, and let T be a syntactic transition from S1 to S2. Then for each descendant L of S1 that is a leaf state, there is a flattened state transition from L to S2. Note in particular that whereas a syntactic state transition may have a parent state as its source, a flattened state transition always has a leaf state as its source. This distinction between syntactic and flattened state transitions will be useful when we discuss entry and exit actions in the following sections.
Internal transitions: Internal transitions are flattened and inherited like other transitions, except that there is no target state. When a parent state S defines an internal transition, the following occurs:
-
There is one flattened transition for each leaf state that that is a descendant of S.
-
The behavior of each flattened transition is to stay in S and do the actions listed in the transition. There is no state change, and no entry or exit actions are done.
-
As usual, any of these flattened transitions may be overridden by behavioral polymorphism.
10.6.3. Entry and Exit Actions
In previous sections on entry and exit actions and on self transitions, we explained the order in which actions occur during a transition between states without hierarchy. Each of the behaviors described there is a special case of a more general behavior for state machines with hierarchy, which we now describe.
General behavior: Suppose, in the course of running an instance of a state machine M, a flattened state transition T occurs from state L to state S. By the definition of a flattened state transition, we know that L is a leaf state. When carrying out the transition T, the state machine instance will do actions as follows:
-
Compute the least common ancestor of L and S. This is the unique node N of the hierarchy tree of M such that (a) N is an ancestor of L, (b) N is an ancestor of S, and (c) there is no node N' that is a descendant of N and that satisfies properties (a) and (b).
-
Traverse the hierarchy tree upwards from L to N. At each point where the traversal passes out of a state S', in the order of the traversal, do the exit actions of S', if any.
-
Do the actions specified in T, if any.
-
Traverse the hierarchy tree downwards from N to S. At each point where the traversal enters a state S', in the order of the traversal, do the entry actions of S', if any.
For example, suppose that M has a state A with substates B and C, B has substate D, and C has substate E. Suppose that T goes from D to E. Then least common ancestor is A, and the following actions would be done, in the following order: the exit actions of D, the exit actions of B, the actions of T, the entry actions of C, and the entry actions of E.
Remember also that if E is not a leaf state, then T will follow one or more transitions to go to a leaf state. In this case, any actions specified in those transitions are done as well, after the transitions described above, and in the order that the initial transitions are run.
Finally, the algorithm above is described in a way that emphasizes ease of understanding. As stated, it is inefficient because it recomputes the least common ancestor every time a flattened state transition occurs. In fact all the sequences of exit and entry actions for flattened state transitions can be computed before generating code, and it is more efficient to do this. This is how the FPP code generator works. For more details, see the algorithm descriptions on the FPP wiki.
The special case of no hierarchy: The general behavior described above agrees with the special-case behavior that we described in the section on entry and exit actions for state machines without hierarchy. When a state machine M has no hierarchy, every state transition T is a flattened transition that goes from a leaf state L to a leaf state S, both of which are children of M in the hierarchy tree. So we always exit L, do the actions of T, and enter S.
In particular, the general behavior agrees with the behavior that we previously described for self transitions. When L and S are the same leaf state, the least common ancestor of L and S is the parent P of S. So we exit S to go up to P, do the actions of T, and reenter S.
10.6.4. Directly Related States
Let S1 and S2 be states. If S1 is equal to S2, or S1 is an ancestor of S2, or S2 is an ancestor of S1, then we say that S1 and S2 are directly related in the hierarchy tree.
In this section we describe the behavior of transitions between directly related states. Each of the behaviors described below follows from the general behavior presented in the previous section. However, in some cases the behavior may be subtle or surprising.
Flattened transitions to ancestors: When a transition T goes from a leaf state L to a state A that is an ancestor of L, we call T a flattened transition to an ancestor. The least common ancestor of L and A is the parent P of A. Therefore the following behavior occurs:
-
Do exit actions to get from L to P. The last actions will be the exit actions of A, if any.
-
Do the actions of T, if any.
-
Do the entry actions of A, if any.
Syntactic transitions to ancestors:
Consider a state transition T of the form
on s enter A that is defined in the state S,
where A is an ancestor of S.
We call this kind of state transition a
syntactic transition to an ancestor.
If S is a leaf state, then it represents
a flattened transition to the ancestor A.
Otherwise it represents one flattened transition
to the ancestor A for each descendant of S that
is a leaf state.
Because of
behavioral polymorphism, any of the flattened transitions may
be overridden.
Flattened transitions to self: A flattened transition to self is a transition from a leaf state L to itself. This is what we previously called a self transition.
Syntactic transitions to self:
Consider a state transition T of the form
on s enter S that is defined in the state S.
In general we call this kind of state transition a
syntactic transition to self.
If S is a leaf state, then T a flattened
transition to self.
In particular, when there is no hierarchy, every syntactic
transition to self is a self transition.
If S is not a leaf state, then T is flattened
to one or more transitions from leaf states L that are
descendants of S.
Each of these transitions is a flattened transition
to the ancestor S.
Because of
behavioral polymorphism, any of the flattened transitions may
be overridden.
Flattened transitions to descendants: In theory, a flattened transition to a descendant would be a transition from a leaf node L to a descendant D of L. However, leaf nodes have no descendants, so no such transition is possible. We include the category for completeness. It has no members.
Syntactic transitions to descendants:
Consider a state transition T of the form
on s enter D that is defined in the state S,
where D is a descendant of S.
We call this kind of state transition a
syntactic transition to a descendant.
By symmetry with syntactic transitions to ancestors,
you might expect that the first behavior when
making such a transition is to exit and reenter S.
However, this is not what happens.
Instead, T represents one flattened transition
from each leaf state that is a descendant of S.
The flattened transitions have the following properties:
-
If D is a leaf state, then the flattened transition out of D (and only that transition) is a flattened transition to self.
-
Otherwise (a) none of the flattened transitions is a flattened transition to self, and (b) the flattened transitions out of the descendants of D are flattened transitions to the ancestor D.
In either case, because of behavioral polymorphism, any of the flattened transitions may be overridden.
10.6.5. Choices
Like state definitions, choice definitions are hierarchical. That is, you may define a choice inside a state. The names of choices are qualified by the enclosing state names as for the names of substates. For example, you can write this:
state machine M {
...
state S {
...
choice C { ... }
...
}
}The dots represent omitted text needed to make the state machine valid.
In this example, the qualified name of the choice is S.C.
Inside state S, you can refer to the choice as S.C or C.
Outside state S, you must refer to it as S.C.
Initial transitions to choices: When an initial transition I goes to a choice C, C and I must have the same parent P in the hierarchy tree. In addition, each transition out of C must go to a state or choice with parent P; and if it goes to a choice, then each transition out of that choice must go to a state or choice with parent P, and so forth. Another way to say this is that (since no cycles of transitions through choices are allowed) each transition path out of I must go through zero or more choices with parent P to a state with parent P.
For example, this state machine is allowed:
state machine ValidInitialChoice {
guard g
initial enter S1
state S1 {
@ This initial transition is valid: C, S2, and S3 all have parent S1
initial enter C
choice C { if g enter S2 else enter S3 }
state S2
state S3
}
}But this one is not:
state machine InvalidInitialChoice {
guard g
initial enter S1
state S1 {
@ This initial transition is invalid: C has parent S1,
@ but S2 and S3 have parent InvalidInitialChoice
initial enter C
choice C { if g enter S2 else enter S3 }
}
state S2
state S3
}Entry and exit actions: As in the non-hierarchical case, when a transition T of a state machine M goes to or from a choice, entry and exit actions occur as if each choice were a leaf state with no entry or exit actions. For example, suppose that M has a state S with substates A and B, A has a choice C, and B has substate B'. Suppose that T goes from C to B'. Then least common ancestor is S, and the following actions would be done, in the following order: the exit actions of A, the actions of T, the entry actions of B, and the entry actions of B'.
10.7. Constants, Types, and Enums
You can write a constant definition,
type definition, or
enum definition as a state machine member.
For example, here is a state machine M that defines a
constant c as a member:
@ A state machine containing a type definition
state machine M {
constant c = 42
state S
initial enter S
}When you do this, the state machine qualifies
the name of the definition, similarly to the way that a
module qualifies the names of the
definitions it contains.
For example, for the constant c shown in the code above:
-
Inside the definition of
M, you can refer to the constant ascorM.c. -
Outside the definition of
M, you must refer to the constant asM.c.
In general, it is a good idea to put a definition inside a
state machine when the definition logically belongs to the
state machine.
For example, here is a state machine that defines a type
Temperature and then uses that type in a signal and a guard:
@ A state machine that defines a type and uses it in a guard
state machine Device {
@ Define a type Temperature
type Temperature = F32
@ Use the Temperature type in a signal
signal onCmd: Temperature
@ Use the Temperature type in a guard
guard temperatureIsSafe: Temperature
@ Initial transition
initial enter OFF
@ OFF state
state OFF {
@ Enter ON if temperature is safe
on onCmd if temperatureIsSafe enter ON
}
@ ON state
state ON
}In this example, the full name of the type Temperature is Device.Temperature.
In most cases, a qualified name such as Device.Temperature in FPP becomes a
qualified name such as Device::Temperature when translating to C++.
However, the current C++ code generation strategy does not support the
definition of constants and types as members of C++ state machines.
Therefore, in the C++ translation of the previous example, the following
occurs:
-
The state machine
SMbecomes an auto-generated C++ classSMStateMachineBase. -
The type
Temperaturebecomes a C++ typeDevice_Temperature.
Similarly, the FPP constant M.c becomes a C++ constant M_c.
We will have more to say about this issue in the section on
generating C++.
10.8. The State Enum
Every state machine definition implicitly contains an enum definition that defines the leaf states of the state machine. This enum is called the state enum of the state machine. For example, consider the following state machine definition:
state machine S {
signal s
initial enter S1
state S1 { initial enter S2; state S2; on s enter S3 }
state S3
}This state machine implicitly contains the following enum definition:
enum State : U8 {
__FPRIME_UNINITIALIZED
S1_S2
S3
}Note the following:
-
The name of the enum is
State. The enum is defined inside the state machineS, so its qualified name isS.State. -
The associated numeric type of the enum is
U8. This is the smallest unsigned type that can hold all the enumerated constants. In most cases, a state enum will not have more than 255 enumerated constants, and so the numeric type will beU8. If necessary, the analyzer will use the typeU16orU32. -
The first enumerated constant is
__FPRIME_UNINITIALIZED. Every state enum has this constant as its first element. It represents the state of the state machine implementation when FSW comes up, before the initial transition of the state machine is run. This state should never occur during normal FSW operations. -
The other constants are the qualified names of the leaf states of the state machine, in alphabetical order, after replacing
.with_.
In the generated code, the implementation
uses the state enum S.State to represent the current state
of the state machine S.
Only the leaf states are represented, because every
transition at runtime goes from a leaf state to a leaf
state.
Because the enumeration is modeled in FPP, you can
use it in telemetry and event reporting.
10.9. Include Specifiers
State machine definitions can become long, especially when there are many actions, signals, and guards. In this case it can be useful to break up the definition into several files.
For example, suppose you are defining a state machine with
many signals, and you wish to place the signals in a
separate file Signals.fppi.
The suffix .fppi is conventional for included FPP files.
Inside the component definition, you can write the
following state machine member:
include "Signals.fppi"This construct is called an include specifier.
During analysis and translation, the include specifier
is replaced with the signals specified
in Signals.fppi, just as if you had written them
at the point where you wrote the include specifier.
This replacement is called expanding or resolving the
include specifier.
You can use the same technique for actions, guards,
or any other state machine members.
The text enclosed in quotation marks after the keyword
include is a path name relative to the directory of the
file in which the include specifier appears.
The file must exist and must contain state machine members
that can validly appear at the point where the include
specifier appears.
For example, if Signals.fppi contains invalid syntax
or syntax that may not appear inside a state machine,
or if the file Signals.fppi does not exist, then
the specifier include "Signals.fppi" is not valid.
You can also write an include specifier as a member
of a state definition.
For example, here is how you could write the
definition of a state S and specify its
transitions in another file called Transitions.fppi:
state S {
include "Transitions.fppi"
}We discuss include specifiers further in the section on specifying models as files.
11. Defining Components
In F Prime, the component is the basic unit of FSW function. An F Prime component is similar to a class in an object-oriented language. An F Prime FSW application is divided into several component instances, each of which instantiates a component. The component instances communicate by sending and receiving invocations on their ports.
In F Prime, there are three kinds of components: active, queued, and passive. An active component has a thread of control and a message queue. A queued component has a message queue, but no thread of control; control runs on another thread, such as a rate group thread. A passive component has no thread of control and no message queue; it is like a non-threaded function library.
11.1. Component Definitions
An FPP component definition defines an F Prime component. To write a component definition, you write the following:
-
The component kind: one of
active,passive, orqueued. -
The keyword
component. -
The name of the component.
-
A sequence of component members enclosed in curly braces
{…}.
As an example, here is a passive component C with no members:
@ An empty passive component
passive component C {
}A component definition and each of its members is an annotatable element. For example, you can annotate the component as shown above. The members of a component form an element sequence with a semicolon as the optional terminating punctuation. The following sections describe the available component members except for importing port interfaces, which we describe in a separate section.
11.2. Port Instances
A port instance is a component member that specifies an instance of an FPP port used by the instances of the component. Component instances use their port instances to communicate with other component instances.
A port instance instantiates a port. The port definition provides information common to all uses of the port, such as the kind of data carried on the port. The port instance provides use-specific information, such as the name of the instance and the direction of invocation (input or output).
11.2.1. Basic Port Instances
The simplest port instance specifies a kind, a name, and a type. The kind is one of the following:
-
asyncinput: Input to this component that arrives on a message queue, to be dispatched on this component’s thread (if this component is active) or on the thread of another port invocation (if this component is queued). -
syncinput: Input that invokes a handler defined in this component, and run on the thread of the caller. -
guardedinput: Similar to sync input, but the handler is guarded by a mutual exclusion lock. -
output: Output transmitted by this component.
The name is the name of the port instance. The type refers to a port definition.
As an example, here is a passive component F32Adder that
adds two F32 values and produces an F32 value.
@ A port for carrying an F32 value
port F32Value(value: F32)
@ A passive component for adding two F32 values
passive component F32Adder {
@ Input 1
sync input port f32ValueIn1: F32Value
@ Input 2
sync input port f32ValueIn2: F32Value
@ Output
output port f32ValueOut: F32Value
}There are two sync input port instances and one output port
instance.
The kind appears first, followed by the keyword port, the port instance
name, a colon, and the type.
Each port instance is an
annotatable element,
so you can annotate the instances as shown.
As another example, here is an active version of F32Adder
with async input ports:
@ A port for carrying an F32 value
port F32Value(value: F32)
@ An active component for adding two F32 values
active component ActiveF32Adder {
@ Input 1
async input port f32ValueIn1: F32Value
@ Input 2
async input port f32ValueIn2: F32Value
@ Output
output port f32ValueOut: F32Value
}In each case, the adding is done in the target language. For example, in the C++ implementation, you would generate a base class with a virtual handler function, and then override that virtual function in a derived class that you write. For further details about implementing F Prime components, see the F Prime User Manual.
Note on terminology: As explained above, there is a technical
distinction between a port type (defined outside any component, and providing
the type of a port instance)
and a port instance (specified inside a component and instantiating
a port type).
However, it is sometimes useful to refer to a port instance with
the shorter term “port” when there is no danger of confusion.
We will do that in this manual.
For example, we will say that the F32Adder component has three
ports: two async input ports of type F32Value and one output port
of type F32Value.
11.2.2. Rules for Port Instances
The port instances appearing in a component definition must satisfy certain rules. These rules ensure that the FPP model makes sense.
First, no passive component may have an async input
port.
This is because a passive component has no message queue,
so asynchronous input is not possible.
As an example, if we modify the input ports of our F32Adder
to make them async, we get an error.
port F32Value(value: F32)
# Error: Passive component may not have async input
passive component ErroneousF32Adder {
async input port f32ValueIn1: F32Value
async input port f32ValueIn2: F32Value
output port f32ValueOut: F32Value
}Try presenting this code to fpp-check and observe what happens.
Second, an active or queued component must have asynchronous input.
That means it must have at least one async input port;
or it must have an internal port;
or it must have at least one async command; or it must have
at least one state machine instance.
Internal ports, async commands, and state machine instances
are described below.
As an example, if we modify the input ports of our ActiveF32Adder
to make them sync, we get an error, because
there is no async input.
port F32Value(value: F32)
# Error: Active component must have async input
active component ErroneousActiveF32Adder {
sync input port f32ValueIn1: F32Value
sync input port f32ValueIn2: F32Value
output port f32ValueOut: F32Value
}Third, a port type appearing in an async input port
may not have a return type.
This is because returning a value
makes sense only for synchronous input.
As an example, this component definition is illegal:
port P -> U32
active component Error {
# Error: port instance p: P is async input and
# port P has a return type
async input port p: P
}11.2.3. Arrays of Port Instances
When you specify a port instance as part of an FPP component, you are actually specifying an array of port instances. Each instance has a port number, where the port numbers start at zero and go up by one at each successive element. (Another way to say this is that the port numbers are the array indices, and the indices start at zero.)
If you don’t specify a size for the array, as shown in
the previous sections, then the array has size one, and there is a single port
instance with port number zero.
Thus a port instance specifier with no array size acts like a singleton
element.
Alternatively, you can specify an explicit array size.
You do that by writing an expression
enclosed in square brackets [ … ] denoting the size (number of elements)
of the array.
The size expression must evaluate to a numeric value.
As with
array type definitions,
the size goes before the element type.
As an example, here is another version of the F32Adder component, this time
using a single array of two input ports instead of two named ports.
@ A port for carrying an F32 value
port F32Value(value: F32)
@ A passive component for adding two F32 values
passive component F32Adder {
@ Inputs 0 and 1
sync input port f32ValueIn: [2] F32Value
@ Output
output port f32ValueOut: F32Value
}11.2.4. Priority
For async input ports, you may specify a priority.
The priority specification is not allowed for other kinds of ports.
To specify a priority, you write the keyword priority and an
expression that evaluates to a numeric value after the port type.
As an example, here is a modified version of the ActiveF32Adder
with specified priorities:
@ A port for carrying an F32 value
port F32Value(value: F32)
@ An active component for adding two F32 values
@ Uses specified priorities
active component ActiveF32Adder {
@ Input 1 at priority 10
async input port f32ValueIn1: F32Value priority 10
@ Input 2 at priority 20
async input port f32ValueIn2: F32Value priority 20
@ Output
output port f32ValueOut: F32Value
}If an async input port has no specified priority, then the
translator uses a default priority.
The precise meaning of the default priority and of the numeric priorities is
implementation-specific.
In general the priorities regulate the order in which elements are dispatched
from the message queue.
11.2.5. Queue Full Behavior
By default, if an invocation of an async input port causes
a message queue to overflow, then a FSW assertion fails.
A FSW assertion is a condition that must be true in order
for FSW execution to proceed safely.
The behavior of a FSW assertion failure is configurable in the C++
implementation of the F Prime framework; typically it causes a FSW
abort and system reset.
Optionally, you can specify the behavior when a message
received on an async input port causes a queue overflow.
There are three possible behaviors:
-
assert: Fail a FSW assertion (the default behavior). -
block: Block the sender until the queue is available. -
drop: Drop the incoming message and proceed. -
hook: Call a user-specified function and proceed.
To specify queue full behavior, you write one of the keywords assert,
block, drop, or hook after the port type and after the priority
(if any).
As an example, here is the ActiveF32Adder updated with explicit
queue full behavior.
@ A port for carrying an F32 value
port F32Value(value: F32)
@ An active component for adding two F32 values
@ Uses specified priorities
active component ActiveF32Adder {
@ Input 1 at priority 10: Block on queue full
async input port f32ValueIn1: F32Value priority 10 block
@ Input 2: Drop on queue full
async input port f32ValueIn2: F32Value drop
@ Input 3: Call hook function on queue full
async input port f32ValueIn3: F32Value hook
@ Output
output port f32ValueOut: F32Value
}As for priority specifiers, queue full specifiers are allowed only
for async input ports.
11.2.6. Serial Port Instances
When writing a port instance, instead of specifying a named port type,
you may write the keyword serial.
Doing this specifies a serial port instance.
A serial port instance does not specify the type of data that it carries.
It may be connected to a port of any type.
Serial data passes through the port; the data may be converted to or from a
specific type at the other end of the connection.
As an example, here is a passive component for taking a stream of serial data and splitting it (i.e., repeating it by copy) onto several streams:
@ Split factor
constant splitFactor = 10
@ Component for splitting a serial data stream
passive component SerialSplitter {
@ Input
sync input port serialIn: serial
@ Output
output port serialOut: [splitFactor] serial
}By using serial ports, you can send several unrelated types of data over the same port connection. This technique is useful when communicating across a network: on each side of the network connection, a single component can act as a hub that routs all data to and from components on that side. This flexibility comes at the cost that you lose the type compile-time type checking provided by port connections with named types. For more information about serial ports and their use, see the F Prime User Manual.
11.3. Special Port Instances
A special port instance is a port instance that has a special behavior in F Prime. As discussed above, when writing a general port instance, you specify a port kind, a port type, and possibly other information such as array size and priority. Writing a special port instance is a bit different. In this case you specify a predefined behavior provided by the F Prime framework. The special port behaviors fall into six groups: commands, events, telemetry, parameters, time, and data products.
11.3.1. Command Ports
A command is an instruction to the spacecraft to perform an action. Each component instance C that specifies commands has the following high-level behaviors:
-
At FSW startup time, C registers its commands with a component instance called the command dispatcher.
-
During FSW execution, C receives commands from the command dispatcher. For each command received, C executes the command and sends a response back to the command dispatcher.
In FPP, the keywords for the special command behaviors are as follows:
-
commandreg: A port for sending command registration requests. -
commandrecv: A port for receiving commands. -
commandresp: A port for sending command responses.
Collectively, these ports are known as command ports.
To specify a command port, you write one of the keyword pairs
shown above followed by the keyword port and the port name.
As an example, here is a passive component CommandPorts with each
of the command ports:
@ A component for illustrating command ports
passive component CommandPorts {
@ A port for receiving commands
command recv port cmdIn
@ A port for sending command registration requests
command reg port cmdRegOut
@ A port for sending command responses
command resp port cmdResponseOut
}Any component may have at most one of each kind of command port. If a component receives commands (more on this below), then all three ports are required. The port names shown in the example above are standard but not required; you can use any names you wish.
During translation, each command port is converted into a typed port instance with a predefined port type, as follows:
-
commandrecvuses the portFw.Cmd -
commandreguses the portFw.CmdReg -
commandrespuses the portFw.CmdResponse
The F Prime framework provides definitions for these ports
in the directory Fw/Cmd.
For checking simple examples, you can use the following
simplified definitions of these ports:
module Fw {
port Cmd
port CmdReg
port CmdResponse
}For example, to check the CommandPorts component, you can
add these lines before the component definition.
If you don’t do this, or something similar, then the component
definition won’t pass through fpp-check because of the missing ports.
(Try it and see.)
Note that the port definitions shown above are for conveniently checking simple examples only. They are not correct for the F Prime framework and will not work properly with F Prime C++ code generation.
For further information about command registration, receipt, and response, and implementing command handlers, see the F Prime User Manual.
11.3.2. Event Ports
An event is a report that something happened, for example, that a file was successfully uplinked. The special event behaviors, and their keywords, are as follows:
-
event: A port for emitting events as serialized bytes. -
textevent: A port for emitting events as human-readable text (usually used for testing and debugging on the ground).
Collectively, these ports are known as event ports.
To specify an event port, you write one of the keyword groups
shown above followed by the keyword port and the port name.
As an example, here is a passive component EventPorts with each
of the event ports:
@ A component for illustrating event ports
passive component EventPorts {
@ A port for emitting events
event port eventOut
@ A port for emitting text events
text event port textEventOut
}Any component may have at most one of each kind of event port. If a component emits events (more on this below), then both event ports are required.
During translation, each event port is converted into a typed port instance with a predefined port type, as follows:
-
eventuses the portFw.Log -
texteventuses the portFw.LogText
The name Log refers to an event log.
The F Prime framework provides definitions for these ports
in the directory Fw/Log.
For checking simple examples, you can use the following
simplified definitions of these ports:
module Fw {
port Log
port LogText
}For further information about events in F Prime, see the F Prime User Manual.
11.3.3. Telemetry Ports
Telemetry is data regarding the state of the system.
A telemetry port allows a component to emit telemetry.
To specify a telemetry port, you write the keyword telemetry,
the keyword port, and the port name.
As an example, here is a passive component TelemetryPorts with
a telemetry port:
@ A component for illustrating telemetry ports
passive component TelemetryPorts {
@ A port for emitting telemetry
telemetry port tlmOut
}Any component may have at most one telemetry port. If a component emits telemetry (more on this below), then a telemetry port is required.
During translation, each telemetry port is converted into
a typed port instance with the predefined port type
Fw.Tlm.
The F Prime framework provides a definition for this port
in the directory Fw/Tlm.
For checking simple examples, you can use the following
simplified definition of this port:
module Fw {
port Tlm
}For further information about telemetry in F Prime, see the F Prime User Manual.
11.3.4. Parameter Ports
A parameter is a configurable constant that may be updated from the ground. The current parameter values are stored in an F Prime component called the parameter database.
The special parameter behaviors, and their keywords, are as follows:
-
paramget: A port for getting the current value of a parameter from the parameter database. -
paramset: A port for setting the current value of a parameter in the parameter database.
Collectively, these ports are known as parameter ports.
To specify a parameter port, you write one of the keyword groups
shown above followed by the keyword port and the port name.
As an example, here is a passive component ParamPorts with each
of the parameter ports:
@ A component for illustrating parameter ports
passive component ParamPorts {
@ A port for getting parameter values
param get port prmGetOut
@ A port for setting parameter values
param set port prmSetOut
}Any component may have at most one of each kind of parameter port. If a component has parameters (more on this below), then both parameter ports are required.
During translation, each parameter port is converted into a typed port instance with a predefined port type, as follows:
-
paramgetuses the portFw.PrmGet -
paramsetuses the portFw.PrmSet
The F Prime framework provides definitions for these ports
in the directory Fw/Prm.
For checking simple examples, you can use the following
simplified definitions of these ports:
module Fw {
port PrmGet
port PrmSet
}For further information about parameters in F Prime, see the F Prime User Manual.
11.3.5. Time Get Ports
A time get port allows a component to get the system time from a
time component.
To specify a time get port, you write the keywords time get,
the keyword port, and the port name.
As an example, here is a passive component TimeGetPorts with
a time get port:
@ A component for illustrating time get ports
passive component TimeGetPorts {
@ A port for getting the time
time get port timeGetOut
}Any component may have at most one time get port. If a component emits events or telemetry (more on this below), then a time get port is required, so that the events and telemetry points can be time stamped.
During translation, each time get port is converted into
a typed port instance with the predefined port type
Fw.Time.
The F Prime framework provides a definition for this port
in the directory Fw/Time.
For checking simple examples, you can use the following
simplified definition of this port:
module Fw {
port Time
}For further information about time in F Prime, see the F Prime User Manual.
11.3.6. Data Product Ports
A data product is a collection of data that can be stored to an onboard file system, given a priority, and downlinked in priority order. For example, a data product may be an image or a unit of science data. Data products are stored in containers that contain records. A record is a unit of data. A container stores (1) a header that describes the container and (2) a list of records.
The special data product behaviors, and their keywords, are as follows:
-
productget: A port for synchronously requesting a memory buffer to store a container. -
productrequest: A port for asynchronously requesting a buffer to store a container. -
productrecv: A port for receiving a response to an asynchronous buffer request. -
productsend: A port for sending a buffer that stores a container, after the container has been filled with data.
Collectively, these ports are known as data product ports.
To specify a data product port, you write one of the keyword groups
shown above followed by the keyword port and the port name.
To specify a product receive port, you must first write
async, sync or guarded to specify whether the input port
is asynchronous, synchronous, or guarded, as described in
the section on basic port instances.
When specifying an async product receive port, you may
specify a priority behavior
or queue full behavior.
As an example, here is a passive component DataProductPorts with each
of the data product ports:
@ A component for illustrating data product ports
active component DataProductPorts {
@ A port for getting a data product container
product get port productGetOut
@ A port for requesting a data product container
product request port productRequestOut
@ An async port for receiving a requested data product container
async product recv port productRecvIn priority 10 assert
@ A port for sending a filled data product container
product send port productSendOut
}Any component may have at most one of each kind of data product port. If a component defines data products (more on this below), then there must be (1) a product get port or a product request port and (2) a product send port. If there is a product request port, then there must be a product receive port.
During translation, each data product port is converted into a typed port instance with a predefined port type, as follows:
-
productgetuses the portFw.DpGet -
productrequestuses the portFw.DpRequest -
productrecvuses the portFw.DpResponse -
productsenduses the portFw.DpSend
The F Prime framework provides definitions for these ports
in the directory Fw/Dp.
For checking simple examples, you can use the following
simplified definitions of these ports:
module Fw {
port DpGet
port DpRequest
port DpResponse
port DpSend
}For further information about data products in F Prime, see the F Prime design documentation.
11.4. Internal Ports
An internal port is a port that a component can use to send a message to itself. In the ordinary case, when a component sends a message, it invokes an output port that is connected to an async input port. When the output port and input port reside in the same component, it is simpler to use an internal port.
As an example, suppose we have a component that needs to send a message to itself. We could construct such a component in the following way:
@ A data type T
type T
@ A port for sending data of type T
port P(t: T)
@ A component that sends data to itself on an async input port
active component ExternalSelfMessage {
@ A port for sending data of type T
async input port pIn: P
@ A port for receiving data of type T
output port pOut: P
}This works, but if the only user of pIn is
ExternalSelfMessage, it is cumbersome.
We need to declare two ports and connect them.
Instead, we can use an internal port, like this:
@ A data type T
type T
@ A component that sends data to itself on an internal port
active component InternalSelfMessage {
@ An internal port for sending data of type T
internal port pInternal(t: T)
}When the implementation of InternalSelfMessage invokes
the port pInternal, a message goes on its queue.
This corresponds to the behavior of pOut in
ExternalSelfMessage.
Later, when the framework dispatches the message, it
calls a handler function associated with the port.
This corresponds to the behavior of pIn in
ExternalSelfMessage.
So an internal port is like two ports (an output port
and an async input port) fused into one.
When writing an internal port, you do not use a named
port definition.
Instead, you provide the formal parameters directly.
Notice that when defining ExternalSelfMessage we
defined and used the port P, but when defining
InternalSelfMessage we did not.
The formal parameters of an internal port work in the same way
as for a port definition,
except that none of the parameters may be a
reference parameter.
When specifying an internal port, you may specify
priority and
queue full behavior
as for an async input port.
For example, we can add priority and queue full behavior
to pInternal as follows:
@ A data type T
type T
@ A component that sends data to itself on an internal port,
@ with priority and queue full behavior
active component InternalSelfMessage {
@ An internal port for sending data of type T
internal port pInternal(t: T) priority 10 drop
}Internal ports generate async input, so they make sense
only for active and queued components.
As an example, consider the following component
definition:
type T
passive component PassiveInternalPort {
# Internal ports don't make sense for passive components
internal port pInternal(t: T)
}What do you think will happen if you run fpp-check
on this code?
Try it and see.
11.5. Commands
When defining an F Prime component, you may specify one or more commands. When you are operating the FSW, you use the F Prime Ground Data System or another ground data system to send commands to the FSW. On receipt of a command C, a Command Dispatcher component instance dispatches C to the component instance where that command is implemented. The command is handled in a C++ command handler that you write as part of the component implementation.
For complete information about F Prime command dispatch and handling, see the F Prime User Manual. Here we concentrate on how to specify commands in FPP.
11.5.1. Basic Commands
The simplest command consists of a kind followed by the keyword
command and a name.
The kind is one of the following:
-
async: The command arrives on a message queue, to be dispatched on this component’s thread (if this component is active) or on the thread of a port invocation (if this component is queued). -
sync: The command invokes a handler defined in this component, and run on the thread of the caller. -
guarded: Similar to sync input, but the handler is guarded by a mutual exclusion lock.
Notice that the kinds of commands are similar to the kinds of input ports. The name is the name of the command.
As an example, here is an active component called Action
with two commands: an async command START and a sync
command STOP.
@ An active component for performing an action
active component Action {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command input
command recv port cmdIn
@ Command registration
command reg port cmdRegOut
@ Command response
command resp port cmdResponseOut
# ----------------------------------------------------------------------
# Commands
# ----------------------------------------------------------------------
@ Start the action
async command START
@ Stop the action
sync command STOP
}Command START is declared async.
That means that when a START command is dispatched
to an instance of this component, it arrives on a queue.
Later, the F Prime framework takes the message off the queue
and calls the corresponding handler on the thread
of the component.
Command STOP is declared sync.
That means that the command runs immediately on the
thread of the invoking component (for example,
a command dispatcher component).
Because the command runs immediately, its handler
should be very short.
For example, it could set a stop flag and then exit.
Notice that we defined the three
command ports
for this component.
All three ports are required for any component that has commands.
As an example, try deleting one or more of the command ports from the
code above and running the result through fpp-check.
async commands require a message queue, so
they are allowed only for active and queued
components.
As an example, try making the Action component passive and
running the result through fpp-check.
11.5.2. Formal Parameters
When specifying a command, you may specify one or more formal parameters. The parameters are bound to arguments when the command is sent to the spacecraft. Different uses of the same command can have different argument values.
The formal parameters of a command are the same as for a port definition, except for the following:
-
None of the parameters may be a reference parameter.
-
Each parameter must have a displayable type, i.e., a type that the F Prime ground data system knows how to display. For example, the type may not be an abstract type. Nor may it be an array or struct type that has an abstract type as a member type.
As an example, here is a Switch component that has
two states, ON and OFF.
The component has a SET_STATE command for
setting the state.
The command has a single argument state
that specifies the new state.
@ The state enumeration
enum State {
OFF @< The off state
ON @< The on state
}
@ A switch with on and off state
active component Switch {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command input
command recv port cmdIn
@ Command registration
command reg port cmdRegOut
@ Command response
command resp port cmdResponseOut
# ----------------------------------------------------------------------
# Commands
# ----------------------------------------------------------------------
@ Set the state
async command SET_STATE(
$state: State @< The new state
)
}In this example, the enum type State is a displayable type because
its definition is known to FPP.
Try replacing the enum definition with the
abstract type definition type S and see what happens when
you run the model through fpp-check.
Remember to provide
stubs for the special command ports that are required by
fpp-check.
11.5.3. Opcodes
Every command in an F Prime FSW application has an opcode. The opcode is a number that uniquely identifies the command. The F Prime framework uses the opcode when dispatching commands because it is a more compact identifier than the name. The name is mainly for human interaction on the ground.
The opcodes associated with each component C are relative to the component. Typically the opcodes start at zero: that is, the opcodes are 0, 1, 2, etc. When constructing an instance I of component C, the framework adds a base opcode for I to each relative opcode associated with C to form the global opcodes associated with I. That way different instances of C can have different opcodes for the same commands defined in C. We will have more to say about base and relative opcodes when we describe component instances and topologies.
If you specify a command c with no explicit opcode, as in the examples shown in the previous sections, then FPP assigns a default opcode to c. The default opcode for the first command in a component is zero. Otherwise the default opcode for any command is one more than the opcode of the previous command.
It is usually convenient to rely on the default opcodes.
However, you may wish to specify one or more opcodes explicitly.
To do this, you write the keyword opcode followed
by a numeric expression after the command name and after the
formal parameters, if any.
Here is an example:
@ Component for illustrating command opcodes
active component CommandOpcodes {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command input
command recv port cmdIn
@ Command registration
command reg port cmdRegOut
@ Command response
command resp port cmdResponseOut
# ----------------------------------------------------------------------
# Commands
# ----------------------------------------------------------------------
@ This command has default opcode 0x0
async command COMMAND_1
@ This command has explicit opcode 0x10
async command COMMAND_2(a: F32, b: U32) opcode 0x10
@ This command has default opcode 0x11
sync command COMMAND_3
}Within a component, the command opcodes must be unique. For example, this component is incorrect because the opcode zero appears twice:
@ Component for illustrating a duplicate opcode
active component DuplicateOpcode {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command input
command recv port cmdIn
@ Command registration
command reg port cmdRegOut
@ Command response
command resp port cmdResponseOut
# ----------------------------------------------------------------------
# Commands
# ----------------------------------------------------------------------
@ This command has opcode 0x0
async command COMMAND_1
@ Oops! This command also has opcode 0x0
async command COMMAND_2 opcode 0x0
}11.5.4. Priority and Queue Full Behavior
When specifying an async command, you may specify priority and queue full behavior as for an async input port. You put the priority and queue full information after the command name and after the formal parameters and opcode, if any. Here is an example:
type FwSizeStoreType = U16
constant FW_FIXED_LENGTH_STRING_SIZE = 256
@ A component for illustrating priority and queue full behavior for async
@ commands
active component PriorityQueueFull {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command input
command recv port cmdIn
@ Command registration
command reg port cmdRegOut
@ Command response
command resp port cmdResponseOut
# ----------------------------------------------------------------------
# Commands
# ----------------------------------------------------------------------
@ Command with priority
async command COMMAND_1 priority 10
@ Command with formal parameters and priority
async command COMMAND_2(a: U32, b: F32) priority 20
@ Command with formal parameters, opcode, priority, and queue full behavior
async command COMMAND_3(a: string) opcode 0x10 priority 30 drop
}Priority and queue full behavior are allowed only for
async commands.
Try changing one of the commands in the previous example
to sync and see what fpp-check has to say about it.
11.6. Events
When defining an F Prime component, you may specify one or more events. The F Prime framework converts each event into a C++ function that you can call from the component implementation. Calling the function emits a serialized event report that you can store in an on-board file system or send to the ground.
For complete information about F Prime event handling, see the F Prime User Manual. Here we concentrate on how to specify events in FPP.
11.6.1. Basic Events
The simplest event consists of the keyword event, a name, a severity,
and a format string.
The name is the name of the event.
A severity is the keyword severity and one of the following:
-
activityhigh: Spacecraft activity of greater importance. -
activitylow: Spacecraft activity of lesser importance. -
command: An event related to commanding. Primarily used by the command dispatcher. -
diagnostic: An event relating to system diagnosis and debugging. -
fatal: An event that causes the system to abort. -
warninghigh: A warning of greater importance. -
warninglow: A warning of lesser importance.
A format is the keyword format and a literal string for
use in a formatted real-time display or event log.
As an example, here is an active component called BasicEvents
with a few basic events.
@ A component for illustrating basic events
passive component BasicEvents {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Event port
event port eventOut
@ Text event port
text event port textEventOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Events
# ----------------------------------------------------------------------
@ Activity low event
event Event1 severity activity low format "Event 1 occurred"
@ Warning low event
event Event2 severity warning low format "Event 2 occurred"
@ Warning high event
event Event3 severity warning high format "Event 3 occurred"
}Notice that we defined the two
event ports
and a
time get port
for this component.
All three ports are required for any component that has events.
As an example, try deleting one or more of these ports from the
code above and running the result through fpp-check.
11.6.2. Formal Parameters
When specifying an event, you may specify one or more formal parameters. The parameters are bound to arguments when the component instance emits the event. The argument values appear in the formatted text that describes the event.
You specify the formal parameters of an event in the same way as for a command specifier. For each formal parameter, there must be a corresponding replacement field in the format string. The replacement fields for event format strings are the same as for format strings in type definitions. The replacement fields in the format string match the event parameters, one for one and in the same order.
As an example, here is a component with two events, each of which has formal parameters. Notice how the replacement fields in the event format strings correspond to the formal parameters.
@ An enumeration of cases
enum Case { A, B, C }
@ An array of 3 F64 values
array F64x3 = [3] F64
@ A component for illustrating event formal parameters
passive component EventParameters {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Event port
event port eventOut
@ Text event port
text event port textEventOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Events
# ----------------------------------------------------------------------
@ Event 1
@ Sample output: "Event 1 occurred with argument 42"
event Event1(
arg1: U32 @< Argument 1
) \
severity activity high \
format "Event 1 occurred with argument {}"
@ Event 2
@ Sample output: "Saw value [ 0.001, 0.002, 0.003 ] for case A"
event Event2(
case: Case @< The case
value: F64x3 @< The value
) \
severity warning low \
format "Saw value {} for case {}"
}11.6.3. Identifiers
Every event in an F Prime FSW application has a unique numeric identifier. As for command opcodes, the event identifiers for a component are specified relative to the component, usually starting from zero and counting up by one. If you omit the identifier, then FPP assigns a default identifier: zero for the first event in the component; otherwise one more than the identifier of the previous event.
If you wish, you may explicitly specify one or more event
identifiers.
To do this, you write the keyword id followed
by a numeric expression immediately before the keyword format.
Here is an example:
@ Component for illustrating event identifiers
passive component EventIdentifiers {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Event port
event port eventOut
@ Text event port
text event port textEventOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Events
# ----------------------------------------------------------------------
@ Event 1
@ Its identifier is 0x00
event Event1 severity activity low \
id 0x10 \
format "Event 1 occurred"
@ Event 2
@ Its identifier is 0x10
event Event2(
count: U32 @< The count
) \
severity activity high \
id 0x11 \
format "The count is {}"
@ Event 3
@ Its identifier is 0x11
event Event3 severity activity high \
format "Event 3 occurred"
}Within a component, the event identifiers must be unique.
11.6.4. Throttling
Sometimes it is necessary to throttle events, to ensure that they do not flood the system. For example, suppose that the FSW requests some resource R at a rate r of several times per second. Suppose further that if R is unavailable, then the FSW emits a warning event. In this case, we typically do not want the FSW to emit an unbounded number of warnings at rate r; instead, we want it to emit a single warning or a few warnings.
To achieve this behavior, you can write the keyword throttle and a
numeric expression after the format string.
The expression must evaluate to a constant value n, where n is a number
greater than zero.
n is called the maximum throttle count.
After an instance of the component has emitted the event n times, it will
stop emitting the event.
Here is an example:
@ Component for illustrating event throttling
passive component EventThrottling {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Event port
event port eventOut
@ Text event port
text event port textEventOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Events
# ----------------------------------------------------------------------
@ Event 1
event Event1 severity warning high \
format "Event 1 occurred" \
throttle 10
}In this example, event Event1 will be throttled after the component
instance has emitted it ten times.
Once an event is throttled, the component instance will no longer emit the event until the throttling is reset. There are two ways to reset the throttling of an event: manually and automatically.
Manual reset:
To manually reset throttling for events,
you can use a command.
For example, you can define a command CLEAR_EVENT_THROTTLE
that resets throttling for all throttled events.
You can implement this command by calling functions
that reset the throttle counts to zero.
The auto-generated C++ code provides one such function for
each event with throttling.
For details, see the
F Prime User Manual.
Automatic reset:
You can also specify in FPP that the throttling for an event should be reset
automatically after a specified amount of time.
To do this, you write every and a time interval after the maximum throttle
count.
The time interval is a struct
value expression with two members: seconds and useconds.
useconds is short for “microseconds.”
Each member must evaluate to an integer value.
Either or both of the members can be omitted; an omitted member evaluates to
zero.
Here is an example:
@ Component for illustrating event throttling with timeouts
passive component EventThrottlingWithTimeout {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Event port
event port eventOut
@ Text event port
text event port textEventOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Events
# ----------------------------------------------------------------------
@ Event 1
event Event1 severity warning high \
format "Event 1 occurred" \
throttle 10 every { seconds = 2 }
@ Event 2
event Event2 severity warning high \
format "Event 2 occurred" \
throttle 10 every { seconds = 2, useconds = 500000 }
@ Event 3
event Event3 severity warning high \
format "Event 3 occurred" \
throttle 10 every { useconds = 500000 }
}In this example, an instance of EventThrottlingWithTimeout will emit events
at the following rates:
-
Event1: Up to 10 events every 2 seconds. -
Event2: Up to 10 events every 2.5 seconds. -
Event3: Up to 10 events every 0.5 seconds.
11.7. Telemetry
When defining an F Prime component, you may specify one or more telemetry channels. A telemetry channel consists of a data type and an identifier. The F Prime framework converts each telemetry into a C++ function that you can call from the component implementation. Calling the function emits a value on the channel. Each emitted value is called a telemetry point. You can store the telemetry points in an on-board file system or send them the ground.
For complete information about F Prime telemetry handling, see the F Prime User Manual. Here we concentrate on how to specify telemetry channels in FPP.
11.7.1. Basic Telemetry
The simplest telemetry channel consists of the keyword telemetry,
a name, and a data type.
The name is the name of the channel.
The data type is the type of data carried on the channel.
The data type must be a
displayable type.
As an example, here is an active component called BasicTelemetry
with a few basic events.
@ An array of 3 F64 values
array F64x3 = [3] F64
@ A component for illustrating basic telemetry channels
passive component BasicTelemetry {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Telemetry
# ----------------------------------------------------------------------
@ Telemetry channel 1
telemetry Channel1: U32
@ Telemetry channel 2
telemetry Channel2: F64
@ Telemetry channel 3
telemetry Channel3: F64x3
}Notice that we defined a telemetry port and a time get port for this component. Both ports are required for any component that has telemetry.
11.7.2. Identifiers
Every telemetry channel in an F Prime FSW application has a unique numeric identifier. As for command opcodes and event identifiers, the telemetry channel identifiers for a component are specified relative to the component, usually starting from zero and counting up by one. If you omit the identifier, then FPP assigns a default identifier: zero for the first event in the component; otherwise one more than the identifier of the previous channel.
If you wish, you may explicitly specify one or more
telemetry channel identifiers.
To do this, you write the keyword id followed
by a numeric expression immediately after the data type.
Here is an example:
@ An array of 3 F64 values
array F64x3 = [3] F64
@ Component for illustrating telemetry channel identifiers
passive component TlmIdentifiers {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Telemetry
# ----------------------------------------------------------------------
@ Telemetry channel 1
@ Its implied identifier is 0x00
telemetry Channel1: U32
@ Telemetry channel 2
@ Its identifier is 0x10
telemetry Channel2: F64 id 0x10
@ Telemetry channel 3
@ Its implied identifier is 0x11
telemetry Channel3: F64x3
}Within a component, the telemetry channel identifiers must be unique.
11.7.3. Update Frequency
You can specify how often the telemetry is emitted on a channel C. There are two possibilities:
-
always: Emit a telemetry point on C whenever the component implementation calls the auto-generated function F that emits telemetry on C. -
onchange: Emit a telemetry point whenever (1) the implementation calls F and (2) either (a) F has not been called before or (b) the last time that F was called, the argument to F had a different value.
Emitting telemetry on change can reduce unnecessary
activity in the system.
For example, suppose a telemetry channel C counts
the number of times that some event E occurs
in a periodic task,
and suppose that E does not occur on every cycle.
If you declare channel C on change, then your implementation
can call the telemetry emit function for C on every
cycle, and telemetry will be emitted only when
E occurs.
To specify an update frequency, you write the keyword update
and one of the frequency selectors shown above.
The update specifier goes after
the type name and after the channel identifier, if any.
If you don’t specify an update frequency, then the default
value is always.
Here is an example:
@ An array of 3 F64 values
array F64x3 = [3] F64
@ Component for illustrating telemetry channel update specifiers
passive component TlmUpdate {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Telemetry
# ----------------------------------------------------------------------
@ Telemetry channel 1
@ Always emitted
telemetry Channel1: U32
@ Telemetry channel 2
@ Emitted on change
telemetry Channel2: F64 id 0x10 update on change
@ Telemetry channel 3
@ Always emitted
telemetry Channel3: F64x3 update always
}11.7.4. Format Strings
You may specify how a telemetry channel is formatted in the
ground display.
To do this, you write the keyword format and a format string
with one
replacement field.
The replacement field must match the type of the telemetry
channel.
The format specifier comes after the type name, after the
channel identifier, and after the update specifier.
Here is an example:
@ Component for illustrating telemetry channel format specifiers
passive component TlmFormat {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Telemetry
# ----------------------------------------------------------------------
@ Telemetry channel 1
telemetry Channel1: U32 format "{x}"
@ Telemetry channel 2
telemetry Channel2: F64 id 0x10 \
update on change \
format "{.3f}"
@ Telemetry channel 3
telemetry Channel3: F64\
update always \
format "{e}"
}11.7.5. Limits
You may specify limits, or bounds, on the expected values
carried on a telemetry channel.
There are two kinds of limits: low (meaning that the
values on the channel should stay above the limit) and high
(meaning that the values should stay below the limit).
Within each kind, there are three levels of severity:
-
yellow: Crossing the limit is of low concern. -
orange: Crossing the limit is of medium concern. -
red: Crossing the limit is of high concern.
The F Prime ground data system displays an appropriate warning when a telemetry point crosses a limit.
The limit specifiers come after the type name, identifier,
update specifier, and format string.
You specify the low limits (if any) first, and then the high limits.
For the low limits, you write the keyword low followed by a
list of limits in curly braces { … }.
For the high limits, you do the same thing but use the keyword
high.
Each limit is a severity keyword followed by a numeric expression.
Here are some examples:
@ Component for illustrating telemetry channel limits
passive component TlmLimits {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Telemetry
# ----------------------------------------------------------------------
@ Telemetry channel 1
telemetry Channel1: U32 \
low { red 0, orange 1, yellow 2 }
@ Telemetry channel 2
telemetry Channel2: F64 id 0x10 \
update on change \
format "{.3f}" \
low { red -3, orange -2, yellow -1 } \
high { red 3, orange 2, yellow 1 }
@ Telemetry channel 3
telemetry Channel3: F64 \
update always \
format "{e}" \
high { red 3, orange 2, yellow 1 }
}Each limit must be a numeric value. The type of the telemetry channel must be (1) a numeric type; or (2) an array or struct type each of whose members has a numeric type; or (3) an array or struct type each of whose members satisfies condition (1) or condition (2).
11.8. Parameters
When defining an F Prime component, you may specify one or more parameters. A parameter is a typed constant value that you can update by command. For example, it could be a configuration constant for a hardware device or a software algorithm.
F Prime has special support for parameters, including a parameter database component for storing parameters in a non-volatile manner (e.g., on a file system). For complete information about F Prime parameters, see the F Prime User Manual. Here we concentrate on how to specify parameters in FPP.
11.8.1. Basic Parameters
The simplest parameter consists of the keyword param,
a name, and a data type.
The name is the name of the parameter.
The data type is the type of data stored in the parameter.
The data type must be a
displayable type.
As an example, here is an active component called BasicParams
with a few basic parameters.
@ An array of 3 F64 values
array F64x3 = [3] F64
@ A component for illustrating basic parameters
passive component BasicParams {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command receive port
command recv port cmdIn
@ Command registration port
command reg port cmdRegOut
@ Command response port
command resp port cmdResponseOut
@ Parameter get port
param get port prmGetOut
@ Parameter set port
param set port prmSetOut
# ----------------------------------------------------------------------
# Parameters
# ----------------------------------------------------------------------
@ Parameter 1
param Param1: U32
@ Parameter 2
param Param2: F64
@ Parameter 3
param Param3: F64x3
}Notice that we defined the two parameter ports for this component. Both ports are required for any component that has parameters.
Notice also that we defined the
command ports
for this component.
When you add one or more parameters to a component,
F Prime automatically generates commands for (1)
setting the local parameter in the component and (2) saving
the local parameter to a system-wide parameter database.
Therefore, any component that has parameters must have
the command ports.
Try deleting one or more of the command ports from the example
above and see what fpp-check does.
11.8.2. Default Values
You can specify a default value for any parameter. This is the value that F Prime will use if no value is available in the parameter database. If you don’t specify a default value, and no value is available in the database, then attempting to get the parameter produces an invalid value. What happens then is up to the FSW implementation. By providing default values for your parameters, you can avoid handling this case.
Here is the example from the previous section, updated to include default values for the parameters:
@ An array of 3 F64 values
array F64x3 = [3] F64
@ A component for illustrating default parameter values
passive component ParamDefaults {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command receive port
command recv port cmdIn
@ Command registration port
command reg port cmdRegOut
@ Command response port
command resp port cmdResponseOut
@ Parameter get port
param get port prmGetOut
@ Parameter set port
param set port prmSetOut
# ----------------------------------------------------------------------
# Parameters
# ----------------------------------------------------------------------
@ Parameter 1
param Param1: U32 default 1
@ Parameter 2
param Param2: F64 default 2.0
@ Parameter 3
param Param3: F64x3 default [ 1.0, 2.0, 3.0 ]
}11.8.3. Identifiers
Every parameter in an F Prime FSW application has a unique numeric identifier. As for command opcodes, event identifiers, and telemetry channel identifiers, the parameter identifiers for a component are specified relative to the component, usually starting from zero and counting up by one. If you omit the identifier, then FPP assigns a default identifier: zero for the first parameter in the component; otherwise one more than the identifier of the previous parameter.
If you wish, you may explicitly specify one or more
parameter identifiers.
To do this, you write the keyword id followed
by a numeric expression after the data type
and after the default value, if any.
Here is an example:
@ An array of 3 F64 values
array F64x3 = [3] F64
@ A component for illustrating default parameter identifiers
passive component ParamIdentifiers {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command receive port
command recv port cmdIn
@ Command registration port
command reg port cmdRegOut
@ Command response port
command resp port cmdResponseOut
@ Parameter get port
param get port prmGetOut
@ Parameter set port
param set port prmSetOut
# ----------------------------------------------------------------------
# Parameters
# ----------------------------------------------------------------------
@ Parameter 1
@ Its implied identifier is 0x00
param Param1: U32 default 1
@ Parameter 2
@ Its identifier is 0x10
param Param2: F64 default 2.0 id 0x10
@ Parameter 3
@ Its implied identifier is 0x11
param Param3: F64x3 default [ 1.0, 2.0, 3.0 ]
}Within a component, the parameter identifiers must be unique.
11.8.4. Set and Save Opcodes
Each parameter that you specify has two implied commands: one for setting the value bound to the parameter locally in the component, and one for saving the current local value to the system-wide parameter database. The opcodes for these implied commands are called the set and save opcodes for the parameter.
By default, FPP generates set and save opcodes for a parameter P according to the following rules:
-
If no command or parameter appears before P in the component, then the set opcode is 0, and the save opcode is 1.
-
Otherwise, let o be the previous opcode defined in the component (either a command opcode or a parameter save opcode). Then the set opcode is o + 1, and the save opcode is o + 2.
If you wish, you may specify either or both of the set and
save opcodes explicitly.
To specify the set opcode, you write the keywords set opcode
and a numeric expression.
To specify the save opcode, you write the keywords save opcode
and a numeric expression.
The set and save opcodes come after the type name, default
parameter value, and parameter identifier.
If both are present, the set opcode comes first.
When you specify an explicit set or save opcode o, the default value for the next opcode is o + 1. Here is an example:
@ An array of 3 F64 values
array F64x3 = [3] F64
@ A component for illustrating parameter set and save opcodes
passive component ParamOpcodes {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command receive port
command recv port cmdIn
@ Command registration port
command reg port cmdRegOut
@ Command response port
command resp port cmdResponseOut
@ Parameter get port
param get port prmGetOut
@ Parameter set port
param set port prmSetOut
# ----------------------------------------------------------------------
# Parameters
# ----------------------------------------------------------------------
@ Parameter 1
@ Its implied set opcode is 0x00
@ Its implied save opcode is 0x01
param Param1: U32 default 1
@ Parameter 2
@ Its set opcode is 0x10
@ Its save opcode is 0x11
param Param2: F64 \
default 2.0 \
id 0x10 \
set opcode 0x10 \
save opcode 0x11
@ Parameter 3
@ Its set opcode is 0x12
@ Its save opcode is 0x20
param Param3: F64x3 \
default [ 1.0, 2.0, 3.0 ] \
save opcode 0x20
}11.8.5. External Parameters
In the default case, when you specify a parameter P in a component
C, the FPP code generator produces code for storing
and managing P as part of the auto-generated
code for C.
Sometimes it is more convenient to store and manage parameters separately.
For example, you may wish to integrate an F Prime component with a library
that stores and manages its own parameters.
In this case you can specify an external parameter.
An external parameter is like an ordinary parameter (also called
an internal parameter), except that its specifier begins
with the keyword external.
Here is an example component definition that specifies two parameters,
an internal parameter Param1 and an external parameter Param2.
@ A component for illustrating internal and external parameters
passive component ParamExternal {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command receive port
command recv port cmdIn
@ Command registration port
command reg port cmdRegOut
@ Command response port
command resp port cmdResponseOut
@ Parameter get port
param get port prmGetOut
@ Parameter set port
param set port prmSetOut
# ----------------------------------------------------------------------
# Parameters
# ----------------------------------------------------------------------
@ Param1 is an internal parameter
param Param1: U32
@ Param2 is an external parameter
external param Param2: F64 \
default 2.0 \
id 0x10 \
set opcode 0x10 \
save opcode 0x11
}When you specify an external parameter, you are responsible for providing the C++ code that stores and maintains the parameter. The F Prime User Manual explains how to do this.
11.9. Data Products
When defining an F Prime component, you may specify the data products produced by that component. A data product is a collection of related data that is stored onboard and transmitted to the ground. F Prime has special support for data products, including components for (1) managing buffers that can store data products in memory; (2) writing data products to the file system; and (3) cataloging stored data products for downlink in priority order. For more information about these F Prime features, see the F Prime User Manual.
11.9.1. Basic Data Products
In F Prime, a data product is represented as a container. One container holds one data product, and each data product is typically stored in its own file. A container consists of a header, which provides information about the container (e.g., the size of the data payload), and binary data representing a list of serialized records. A record is a unit of data. For a complete specification of the container format, see the F Prime design documentation.
In an F Prime component, you can specify one or more containers
and one or more records.
The simplest container specification consists of the keywords product container
and a name.
The name is the name of the container.
The simplest record specification consists of the keywords product record,
a name, and a data type.
The name is the name of the record.
The data type is the type of the data that the record holds.
The data type must be a
displayable type.
As an example, here is a component called BasicDataProducts that specifies
two records and two containers.
@ A struct type defining some data
struct Data { a: U32, b: F32 }
@ A component for illustrating basic data products
passive component BasicDataProducts {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Product get port
product get port productGetOut
@ Product send port
product send port productSendOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Records
# ----------------------------------------------------------------------
@ Record 1
product record Record1: I32
@ Record 2
product record Record2: Data
# ----------------------------------------------------------------------
# Containers
# ----------------------------------------------------------------------
@ Container 1
product container Container1
@ Container 2
product container Container2
}The FPP back end uses this specification to generate code for requesting buffers to hold containers and for serializing records into containers. See the F Prime design documentation for the details.
Note the following:
-
Records are not specific to containers. For example, with the specification shown above, you can serialize instances of
Record1andRecord2into either or both ofContainer1andContainer2. -
Like telemetry channels, F Prime containers are component-centric. A component can request containers that it defines, and it can fill those containers with records that it defines. It cannot use records or containers defined by another component.
-
If a component has container specifier, then it must have at least one record specifier, and vice versa.
11.9.2. Identifiers
Every record in an F Prime FSW application has a unique numeric identifier. As for command opcodes, event identifiers, telemetry channel identifiers, and parameters, the record identifiers for a component are specified relative to the component, usually starting from zero and counting up by one. If you omit the identifier, then FPP assigns a default identifier: zero for the first event in the component; otherwise one more than the identifier of the previous parameter. The same observations apply to containers and container identifiers.
If you wish, you may explicitly specify one or more
container or record identifiers.
To do this, you write the keyword id followed
by a numeric expression at the end of the container
or record specifier.
Here is an example:
@ A struct type defining some data
struct Data { a: U32, b: F32 }
@ A component for illustrating data product identifiers
passive component DataProductIdentifiers {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Product get port
product get port productGetOut
@ Product send port
product send port productSendOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Records
# ----------------------------------------------------------------------
@ Record 1
@ Its implied identifier is 0x00
product record Record1: I32
@ Record 2
@ Its identifier is 0x10
product record Record2: Data id 0x10
# ----------------------------------------------------------------------
# Containers
# ----------------------------------------------------------------------
@ Container 1
@ Its identifier is 0x10
product container Container1 id 0x10
@ Container 2
@ Its implied identifier is 0x11
product container Container2
}Within a component, the record identifiers must be unique, and the container identifiers must be unique.
11.9.3. Array Records
In the basic form of a record described above, each record that
does not have
string type
has a fixed, statically-specified size.
The record may contain an array (e.g., an
array type
or a struct type with a
member array),
but the size of the array must be specified in the model.
To specify a record that is a dynamically-sized array, you put
the keyword array after the type specifier for the record.
For example:
@ A struct type defining some data
struct Data { a: U32, b: F32 }
@ A component for illustrating array records
passive component ArrayRecords {
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Product get port
product get port productGetOut
@ Product send port
product send port productSendOut
@ Time get port
time get port timeGetOut
# ----------------------------------------------------------------------
# Records
# ----------------------------------------------------------------------
@ A data record
@ It holds one element of type Data
product record DataRecord: Data
@ A data array record
@ It holds an array of elements of type Data
product record DataArrayRecord: Data array
# ----------------------------------------------------------------------
# Containers
# ----------------------------------------------------------------------
@ A container
product container Container
}In this example, a record with name DataArrayRecord holds
an array of elements of type Data.
The number of elements is unspecified in the model;
it is provided when the record is serialized into a container.
11.10. State Machine Instances
A state machine instance is a component member that instantiates an FPP state machine. The state machine instance becomes part of the component implementation.
For example, here is a simple async component that has one state machine instance and one async input port for driving the state machine:
@ An external state machine
state machine M
@ A component with a state machine
active component StateMachine {
@ A port for driving the state machine
async input port schedIn: Svc.Sched
@ An instance of state machine M
state machine instance m: M
}When a state machine instance m is part of a component C, each instance c of C sends m signals to process as it runs. Signals occur in response to commands or port invocations received by c, and they tell m when to change state. c puts the signals on its queue, and m dispatches them. Therefore, if a component C has a state machine instance member m, then its instances c must have queues, i.e., C must be active or queued.
As with internal ports, you may specify priority and queue full behavior associated with the signals dispatched by a state machine instance. For example, we can revise the example above as follows:
@ An external state machine
state machine M
@ A component with a state machine
active component StateMachine {
@ A port for driving the state machine
async input port schedIn: Svc.Sched
@ An instance of state machine M
state machine instance m: M priority 10 drop
}As discussed above, state machine definitions may be internal (specified in FPP) or external (specified by an external tool). For more details about the C++ code generation for instances of internal state machines, see the F Prime design documentation.
11.11. Constants, Types, Enums, and State Machines
You can write a constant definition,
type definition,
enum definition,
or
state machine definition
as a component member.
When you do this, the component qualifies
the name of the definition, similarly to the way that a
module or
state machine qualifies the names of the
definitions it contains.
For example, if you define a type T inside a component
C, then
-
Inside the definition of
C, you can refer to the type asTorC.T. -
Outside the definition of
C, you must refer to the type asC.T.
As an example, here is the SerialSplitter component
from the section on
serial port instances, where we have moved the
definition of the constant splitFactor
into the definition of the component.
@ Component for splitting a serial data stream
passive component SerialSplitter {
# ----------------------------------------------------------------------
# Constants
# ----------------------------------------------------------------------
@ Split factor
constant splitFactor = 10
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Input
sync input port serialIn: serial
@ Output
output port serialOut: [splitFactor] serial
}As another example, here is the Switch component from the section on
command formal parameters, where we have moved the definition of
the enum State into the component:
@ A switch with on and off state
active component Switch {
# ----------------------------------------------------------------------
# Types
# ----------------------------------------------------------------------
@ The state enumeration
enum State {
OFF @< The off state
ON @< The on state
}
# ----------------------------------------------------------------------
# Ports
# ----------------------------------------------------------------------
@ Command input
command recv port cmdIn
@ Command registration
command reg port cmdRegOut
@ Command response
command resp port cmdResponseOut
# ----------------------------------------------------------------------
# Commands
# ----------------------------------------------------------------------
@ Set the state
async command SET_STATE(
$state: State @< The new state
)
}In general, it is a good idea to put a definition inside a component when the definition logically belongs to the component. The name scoping mechanism emphasizes the hierarchical relationship and prevents name clashes.
In most cases, a qualified name such as Switch.State
in FPP becomes a qualified name such as Switch::State when translating
to C++.
However, the current C++ code generation strategy does not
support the definition
of constants, types, and state machines as
members of C++ components.
Therefore, when translating the previous example to C++,
the following occurs:
-
The component
Switchbecomes an auto-generated C++ classSwitchComponentBase. -
The type
Statebecomes a C++ classSwitch_State.
Similarly, the FPP constant SerialSplitter.splitFactor
becomes a C++ constant SerialSplitter_SplitFactor.
We will have more to say about this issue in the section on
generating C++.
If you define a state machine inside a component, and you
define a constant, type, or enum
inside a state machine,
then the name prefixes are joined in the obvious way.
For example, a type T defined inside a state machine SM defined
inside a component C has the name C_SM_T.
11.12. Include Specifiers
Component definitions can become long, especially when there are many commands, events, telemetry channels, and parameters. In this case it can be useful to break up the definition into several files.
For example, suppose you are defining a component with
many commands, and you wish to place the commands in a
separate file Commands.fppi.
The suffix .fppi is conventional for included FPP files.
Inside the component definition, you can write the
following component member:
include "Commands.fppi"This construct is called an include specifier.
During analysis and translation, the include specifier
is replaced with the commands specified
in Commands.fppi, just as if you had written them
at the point where you wrote the include specifier.
This replacement is called expanding or resolving the
include specifier.
You can use the same technique for events, telemetry,
parameters, or any other component members.
The text enclosed in quotation marks after the keyword
include is a path name relative to the directory of the
file in which the include specifier appears.
The file must exist and must contain component members
that can validly appear at the point where the include
specifier appears.
For example, if Commands.fppi contains invalid syntax
or syntax that may not appear inside a component,
or if the file Commands.fppi does not exist, then
the specifier include "Commands.fppi" is not valid.
Include specifiers can also appear at the top level of a model, inside a module definition, inside a state machine definition, or inside a topology definition. We discuss include specifiers further in the section on specifying models as files.
11.13. Matched Ports
Some F Prime components employ the following pattern:
-
The component has a pair of port arrays, say
p1andp2. The two arrays have the same number of ports. -
For every connection between
p1and another component instance, there must be a matching connection between that component instance andp2. -
The matched pairs in item 2 must be connected to the same port numbers at
p1andp2.
In this case we call p1 and p2 a pair of
matched ports.
For example:
-
The standard Command Dispatcher component has matched ports
compCmdRegfor receiving command registration andcompCmdSendfor sending commands. -
The standard Health component has matched ports
PingSendfor sending health ping messages andPingReturnfor receiving responses to the ping messages.
FPP provides special support for matched ports.
Inside a component definition, you can write
match p1 with p2, where p1 and p2 are the names of
port instances
defined in the component.
When you do this, the following occurs:
-
The FPP translator checks that
p1andp2have the same number of ports. If not, an error occurs. -
When automatically numbering a topology, the translator ensures that the port numbers match in the manner described above.
For example, here is a simplified version of the Health component:
@ Number of health ping ports
constant numPingPorts = 10
queued component Health {
@ Ping output port
output port pingOut: [numPingPorts] Svc.Ping
@ Ping input port
async input port pingIn: [numPingPorts] Svc.Ping
@ Corresponding port numbers of pingOut and pingIn must match
match pingOut with pingIn
}This component defines a pair of matched ports
pingOut and pingIn.
12. Defining and Using Port Interfaces
A common pattern in F Prime is to use an identical set of port instances in the definitions of each of several components. For example, each of several driver components may specify an identical set of ports for sending and receiving data. Such a set of port instances is called a port interface (interface for short). FPP has special support for defining and using port interfaces, which we describe in this section.
12.1. Defining Port Interfaces
A port interface definition defines a port interface. To write a port interface definition, you write the following:
-
The keyword
interface. -
The name of the interface.
-
A sequence of port interface members enclosed in curly braces
{…}.
A port interface member may directly specify a
general port instance or a
special port instance.
For example, here is a port interface representing a binary operation
that takes two F32 inputs and produces an F32 output:
@ A port for carrying an F32 value
port F32Value(value: F32)
@ A priority constant for async F32 binary operation input
constant AsyncF32BinopInputPriority = 10
@ An active component for adding two F32 values with specified priorities
interface AsyncF32Binop {
@ Input 1 at priority 10
async input port f32ValueIn1: F32Value priority AsyncF32BinopInputPriority
@ Input 2 at priority 20
async input port f32ValueIn2: F32Value priority AsyncF32BinopInputPriority
@ Output
output port f32ValueOut: F32Value
}This interface represents the input and output ports for any binary operation: addition, multiplication, etc. An interface member may also import the definition of another interface; we describe this option below.
An interface definition and each of its members is an annotatable element. For example, you can annotate the interface as shown above. The members of a interface form an element sequence with a semicolon as the optional terminating punctuation.
In general, port instances that appear in port interfaces must follow the same rules as port instances that appear in components. For example, each port name appearing in the interface must be distinct. The rules specific to active, passive, and queued components do not apply to interfaces; those are checked when the interface is used in a component, as described in the next section.
12.2. Using Port Interfaces in Component Definitions
Once you have defined a port interface, you can use it in a component definition.
To do this you write a component
member consisting of the keyword import followed by the interface name.
For example:
@ An active component for adding two F32 values
active component ActiveF32Adder {
@ Import the AsyncF32Binop interface
import AsyncF32Binop
}This component is identical to the ActiveF32Adder component
that we defined in the section on
basic port instances, except that we have factored the input
and output ports into an interface.
We can then use the same interface to define an ActiveF32Multiplier
component:
@ An active component for multiplying two F32 values
active component ActiveF32Multiplier {
@ Import the AsyncF32Binop interface
import AsyncF32Binop
}This component is identical to ActiveF32Adder, except
that it performs multiplication instead of addition.
In general, a component member import I member is analyzed by (1)
resolving the interface I to a set of port instances
and (2) adding each of the port instances to the component.
After this resolution, all the rules for component definition
must be obeyed.
For example, this component definition is illegal,
because it has a duplicate port name:
port P
interface I {
sync input port p: P
}
passive component C {
@ Port instance p is imported here
import I
@ Port instance name p is a duplicate here
sync input port p: P
}12.3. Using Port Interfaces in Interface Definitions
You can import a port interface into another interface. For example:
port P
interface I1 {
sync input port p1: P
}
interface I2 {
import I1
sync input port p2: P
}Either I1 or I2 may be imported into a component
or into another interface.
Interface I2 is functionally equivalent to the
following:
port P
interface I2 {
sync input port p1: P
sync input port p2: P
}13. Defining Component Instances
As discussed in the section on defining-components, in F Prime you define components and instantiate them. Then you construct a topology, which is a graph that specifies the connections between the components. This section explains how to define component instances. In the next section, we will explain how to construct topologies.
13.1. Component Instance Definitions
To instantiate a component, you write a component instance definition. The form of a component instance definition depends on the kind of the component you are instantiating: passive, queued, or active.
13.1.1. Passive Components
To instantiate a passive component, you write the following:
-
The keyword
instance. -
The name of the instance.
-
A colon
:. -
The name of a component definition.
-
The keywords
baseid. -
An expression denoting the base identifier associated with the component instance.
The base identifier must resolve to a number. The FPP translator adds this number to each of the component-relative command opcodes, event identifiers, telemetry channel identifiers, and parameter identifiers specified in the component, as discussed in the previous section. The base identifier for the instance plus the component-relative opcode or identifier for the component gives the corresponding opcode or identifier for the instance.
Here is an example:
module Sensors {
@ A component for sensing engine temperature
passive component EngineTemp {
@ Schedule input port
sync input port schedIn: Svc.Sched
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
@ Impulse engine temperature
telemetry ImpulseTemp: F32
@ Warp core temperature
telemetry WarpTemp: F32
}
}
module FSW {
@ Engine temperature instance
instance engineTemp: Sensors.EngineTemp base id 0x100
}We have defined a passive component Sensors.EngineTemp with three ports:
a schedule input port for driving the component periodically on a rate group,
a time get port for getting the time, and a telemetry port
for reporting telemetry.
(For more information on rate groups and the use of Svc.Sched
ports, see the
F
Prime documentation.)
We have given the component two telemetry channels:
ImpulseTemp for reporting the temperature of the impulse engine,
and WarpTemp for reporting the temperature of the warp core.
Next we have defined an instance FSW.engineTemp of component Sensors.EngineTemp.
Because the instance definition is in a different module from the
component definition, we must refer to the component by its
qualified name Sensors.EngineTemp.
If we wrote
instance engineTemp: EngineTemp base id 0x100the FPP compiler would complain that the symbol EngineTemp is undefined
(try it and see).
We have specified that the base identifier of instance FSW.engineTemp
is the hexadecimal number 0x100 (256 decimal).
In the component definition, the telemetry channel ImpulseTemp
has relative identifier 0, and the telemetry channel WarpTemp
has relative identifier 1.
Therefore the corresponding telemetry channels for the instance
FSW.engineTemp have identifiers 0x100 and 0x101 (256 and 257)
respectively.
For consistency, the base identifier is required for all component instances, even instances that define no dictionary elements (commands, events, telemetry, or parameters). For each component instance I, the range of numbers between the base identifier and the base identifier plus the largest relative identifier is called the identifier range of I. If a component instance defines no dictionary elements, then the identifier range is empty. All the numbers in the identifier range of I are reserved for instance I (even if they are not all used). No other component instance may have a base identifier that lies within the identifier range of I.
For example, this code is illegal:
module FSW {
@ Temperature sensor for the left engine
instance leftEngineTemp: Sensors.EngineTemp base id 0x100
@ Temperature sensor for the right engine
instance rightEngineTemp: Sensors.EngineTemp base id 0x101
}The base identifier 0x101 for rightEngineTemp is inside the
identifier range for leftEngineTemp, which goes from
0x100 to 0x101, inclusive.
13.1.2. Queued Components
Instantiating a queued component is just like instantiating
a passive component, except that you must also specify
a queue size for the instance.
You do this by writing the keywords queue size and
the queue size after the base identifier.
Here is an example:
module Sensors {
@ A port for calibration input
port Calibration(cal: F32)
@ A component for sensing engine temperature
queued component EngineTemp {
@ Schedule input port
sync input port schedIn: Svc.Sched
@ Calibration input
async input port calibrationIn: Calibration
@ Telemetry port
telemetry port tlmOut
@ Time get port
time get port timeGetOut
@ Impulse engine temperature
telemetry ImpulseTemp: F32
@ Warp core temperature
telemetry WarpTemp: F32
}
}
module FSW {
@ Engine temperature sensor
instance engineTemp: Sensors.EngineTemp base id 0x100 \
queue size 10
}In the component definition, we have revised the example from the previous
section so that
the EngineTemp component is queued instead of passive,
and we have added an async input port for calibration input.
In the component instance definition, we have specified a queue size of 10.
13.1.3. Active Components
Instantiating an active component is like instantiating a queued component, except that you may specify additional parameters that configure the OS thread associated with each component instance.
Queue size, stack size, and priority:
When instantiating an active component, you must
specify a queue size, and you may specify either or both of
a stack size and priority.
You specify the queue size in the same way as for a queued component.
You specify the stack size by writing the keywords stack size
and the desired stack size in bytes.
You specify the priority by writing the keyword priority
and a numeric priority.
The priority number is passed to the OS operation for creating
the thread, and its meaning is OS-specific.
Here is an example:
module Utils {
@ A component for compressing data
active component DataCompressor {
@ Uncompressed input data
async input port bufferSendIn: Fw.BufferSend
@ Compressed output data
output port bufferSendOut: Fw.BufferSend
}
}
module FSW {
module Default {
@ Default queue size
constant queueSize = 10
@ Default stack size
constant stackSize = 10 * 1024
}
@ Data compressor instance
instance dataCompressor: Utils.DataCompressor base id 0x100 \
queue size Default.queueSize \
stack size Default.stackSize \
priority 30
}We have defined an active component Utils.DataCompressor
for compressing data.
We have defined an instance of this component called
FSW.dataCompressor.
Our instance has base identifier 0x100, the default
queue size, the default stack size, and priority 30.
We have used
constant definitions for
the default queue and stack sizes.
We could also have omitted either or both of the stack size and priority
specifiers.
When you omit the stack size or priority from a component instance
definition, F Prime supplies a default value appropriate to the
target platform.
With implicit stack size and priority, the dataCompressor
instance looks like this:
instance dataCompressor: Utils.DataCompressor base id 0x100 \
queue size Default.queueSizeCPU affinity: When defining an active component, you may specify a CPU affinity. The CPU affinity is a number whose meaning depends on the platform. Usually it is an instruction to the operating system to run the thread of the active component on a particular CPU, identified by number.
To specify CPU affinity, you write the keyword cpu
and the CPU number after the queue size, the stack size (if any),
and the priority specifier (if any).
For example:
instance dataCompressor: Utils.DataCompressor base id 0x100 \
queue size Default.queueSize \
stack size Default.stackSize \
priority 30 \
cpu 0This example is the same as the previous dataCompressor
instance, except that we have specified that the thread
associated with the instance should run on CPU 0.
With implicit stack size and priority, the example looks like this:
instance dataCompressor: Utils.DataCompressor base id 0x100 \
queue size Default.queueSize \
cpu 013.2. Specifying the Implementation
When you define a component instance I, the FPP translator needs to know the following information about the C++ implementation of I:
-
The type (i.e., the name of the C++ class) that defines the implementation.
-
The location of the C++ header file that declares the implementation class.
In most cases, the translator can infer this information. However, in some cases you must specify it manually.
The implementation type:
The FPP translator can automatically infer the implementation
type if its qualified C++ class name matches the qualified
name of the FPP component.
For example, the C++ class name A::B matches the FPP component
name A.B.
More generally, modules in FPP become namespaces in C++, so
dot qualifiers in FPP become double-colon qualifiers in C++.
If the names do not match, then you must provide the type
associated with the implementation.
You do this by writing the keyword type after the base identifier,
followed by a string
specifying the implementation type.
For example, suppose we have a C++ class Utils::SpecialDataCompressor,
which is a specialized implementation of the FPP component
Utils.DataCompressor.
By default, when we specify Utils.DataCompressor as the component name, the
translator infers Utils::DataCompressor as the implementation type.
Here is how we specify the implementation type Utils::SpecialDataCompressor:
instance dataCompressor: Utils.DataCompressor base id 0x100 \
type "Utils::SpecialDataCompressor" \
queue size Default.queueSize \
cpu 0The header file: The FPP translator can automatically locate the header file for I if it conforms to the following rules:
-
The name of the header file is
Name.hpp, whereNameis the name of the component in the FPP model, without any module qualifiers. -
The header file is located in the same directory as the FPP source file that defines the component.
For example, the F Prime repository contains a reference FSW implementation
with instances defined in the file Ref/Top/instances.fpp.
One of the instances is SG1.
Its definition reads as follows:
instance SG1: Ref.SignalGen base id 0x2100 \
queue size Default.queueSizeThe FPP component Ref.SignalGen is
defined in the directory Ref/SignalGen/SignalGen.fpp,
and the implementation class Ref::SignalGen is declared in
the header file Ref/SignalGen/SignalGen.hpp.
In this case, the header file follows rules (1) and (2)
stated above, so the FPP translator can automatically locate
the file.
If the implementation header file does not follow
rules (1) and (2) stated above, then you must specify
the name and location of the header file by hand.
You do that by writing the keyword at followed by
a string
specifying the header file path.
The header file path is relative to the directory
containing the source file that defines the component
instance.
For example, the F Prime repository has a directory
Svc/Time that contains an FPP model for a component Svc.Time.
Because the C++ implementation for this component
is platform-specific, the directory Svc/Time doesn’t
contain any implementation.
Instead, when instantiating the component, you have to
provide the header file to an implementation located
in a different directory.
The F Prime repository also provides a Linux-specific implementation
of the Time component in the directory Svc/LinuxTime.
The file Ref/Top/instances.fpp contains an instance definition
linuxTime that reads as follows:
instance linuxTime: Svc.Time base id 0x4500 \
type "Svc::LinuxTime" \
at "../../Svc/LinuxTime/LinuxTime.hpp"This definition says to use the implementation of the component
Svc.Time with C++ type name Svc::LinuxTime defined in the header
file ../../Svc/LinuxTime/LinuxTime.hpp.
13.3. Init Specifiers
In an F Prime FSW application, each component instance I
has some associated C++ code
for setting up I when FSW starts up
and tearing down I when FSW exits.
Much of this code can be inferred from the FPP model,
but some of it is implementation-specific.
For example, each instance of the standard F Prime command sequencer
component has a method allocateBuffer that the FSW must
call during setup to allocate the sequence buffer
for that instance.
The FPP model does not represent this function;
instead, you have to provide
the function call directly in C++.
To do this, you write one or more init specifiers as part of a component instance definition. An init specifier names a phase of the setup or teardown process and provides a snippet of literal C++ code. The FPP translator pastes the snippet into the setup or teardown code according to the phase named in the specifier. (Strictly speaking, the init specifier should be called a "setup or teardown specifier." However, most of the code is in fact initialization code, and so FPP uses "init" as a shorthand name.)
13.3.1. Execution Phases
The FPP translator uses init specifiers when it generates code for an F Prime topology. We will have more to say about topology generation in the next section. For now, you just need to know the following:
-
A topology is a unit of an FPP model that specifies the top-level structure of an F Prime application (the component instances and their connections).
-
Each topology has a name, which we will refer to here generically as T.
-
When generating C++ code for topology T, the code generator produces files T
TopologyAc.hppand TTopologyAc.cpp.
The generated code in T TopologyAc.hpp and T TopologyAc.cpp
is divided into several phases of execution.
Table Execution Phases shows the execution phases
recognized by the FPP code generator.
In this table, T is the name of a topology and I is the
name of a component instance.
The columns of the table have the following meanings:
-
Phase: The symbol denoting the execution phase. These symbols are the enumerated constants of the enum
Fpp.ToCpp.Phasesdefined inFpp/ToCpp.fppin the F Prime repository. -
Generated File: The generated file for topology T that contains the definition: either T
TopologyAc.hpp(for compile-time symbols) or TTopologyAc.cpp(for link-time symbols). -
Intended Use: The intended use of the C++ code snippet associated with the instance I and the phase.
-
Where Placed: Where FPP places the code snippet in the generated file.
-
Default Code: Whether FPP generates default code if there is no init specifier for instance I and for this phase. If there is an init specifier, then it replaces any default code.
| Phase | Generated File | Intended Use | Where Placed | Default Code |
|---|---|---|---|---|
|
T |
C++ constants for use in constructing and initializing an instance I. |
In the namespace |
None. |
|
T |
Statically declared C++ objects for use in constructing and initializing instance I. |
In the namespace |
None. |
|
T |
A constructor for an instance I that has a non-standard constructor format. |
In an anonymous (file-private) namespace. |
The standard constructor call for I. |
|
T |
Initialization code for an instance I that has a non-standard initialization format. |
In the file-private function |
The standard call to |
|
T |
Implementation-specific configuration code for an instance I. |
In the file-private function |
None. |
|
T |
Code for registering the commands of I (if any) with the command dispatcher. Required only if I has a non-standard command registration format. |
In the file-private function |
The standard call to |
|
T |
Code for reading parameters from a file. Ordinarily used only when I is the parameter database. |
In the file-private function |
None. |
|
T |
Code for loading parameter values from the parameter database. Required only if I has a non-standard parameter-loading format. |
In the file-private function |
The standard call to |
|
T |
Code for starting the task (if any) of I. |
In the file-private function |
The standard call to |
|
T |
Code for stopping the task (if any) of I. |
In the file-private function |
The standard call to |
|
T |
Code for freeing the thread associated with I. |
In the file-private function |
The standard call to |
|
T |
Code for deallocating the allocated memory (if any) associated with I. |
In the file-private function |
None. |
You will most often need to write code for configConstants,
configObjects, and configComponents.
These phases often require implementation-specific input that
cannot be provided in any other way, except to write an init specifier.
In theory you should never have to write code for instances
or initComponents — this code can be be standardized — but in practice not all F Prime components conform to the standard,
so you may have to override the default.
You will typically not have to write code for regCommands,
readParameters, and loadParameters — the framework can generate
this code automatically — except that the parameter database
instance needs one line of special code for reading its parameters.
Code for startTasks, stopTasks,
and freeThreads is required only if the user-written implementation of
a component instance manages its own F Prime task.
If you use a standard F Prime active component, then the framework
manages the task, and this code is generated automatically.
Code for tearDownComponents is required only if a component
instance needs to deallocate memory or release resources on program exit.
13.3.2. Writing Init Specifiers
You may write one or more init specifiers as part of a component instance definition. The init specifiers, if any, come at the end of the definition and must be enclosed in curly braces. The init specifiers form an element sequence with a semicolon as the optional terminating punctuation.
To write an init specifier, you write the following:
-
The keyword
phase. -
The execution phase of the init specifier.
-
A string that provides the code snippet.
It is usually convenient, but not required, to use a multiline string for the code snippet.
As an example, here is the component instance definition for the
command sequencer instance cmdSeq from the
F Prime system reference deployment:
instance cmdSeq: Svc.CmdSequencer base id 0x0700 \
queue size Default.queueSize \
stack size Default.stackSize \
priority 100 \
{
phase Fpp.ToCpp.Phases.configConstants """
enum {
BUFFER_SIZE = 5*1024
};
"""
phase Fpp.ToCpp.Phases.configComponents """
cmdSeq.allocateBuffer(
0,
Allocation::mallocator,
ConfigConstants::SystemReference_cmdSeq::BUFFER_SIZE
);
"""
phase Fpp.ToCpp.Phases.tearDownComponents """
cmdSeq.deallocateBuffer(Allocation::mallocator);
"""
}The code for configConstants provides a constant BUFFER_SIZE
that is used in the configComponents phase.
The code generator places this code snippet in the
namespace ConfigConstants::SystemReference_cmdSeq.
Notice that the second part of the namespace uses the
fully qualified name SystemReference::cmdSeq, and it replaces
the double colon :: with an underscore _ to generate
the name.
We will explain this behavior further in the section on
generation of names.
The code for configComponents calls allocateBuffer, passing
in an allocator object that is declared elsewhere.
(In the section on
implementing deployments, we will explain where this allocator
object is declared.)
The code for tearDownComponents calls deallocateBuffer to
deallocate the sequence buffer, passing in the allocator
object again.
As another example, here is the instance definition for the parameter
database instance prmDb from the system reference deployment:
instance prmDb: Svc.PrmDb base id 0x0D00 \
queue size Default.queueSize \
stack size Default.stackSize \
priority 96 \
{
phase Fpp.ToCpp.Phases.instances """
Svc::PrmDb prmDb(FW_OPTIONAL_NAME("prmDb"), "PrmDb.dat");
"""
phase Fpp.ToCpp.Phases.readParameters """
prmDb.readParamFile();
"""
}Here we provide code for the instances phase because the constructor
call for this component is nonstandard — it takes the parameter
file name as an argument.
In the readParameters phase, we provide the code for reading the parameters
from the file.
As discussed above, this code is needed only for the parameter database
instance.
When writing init specifiers, you may read (but not modify) a special value
state that you define in a handwritten main function.
This value lets you pass application-specific information from the
handwritten code to the auto-generated code.
We will explain the special state value further in the
section on implementing deployments.
For more examples of init specifiers in action, see the rest of
the file SystemReference/Top/instances.fpp in the F Prime repository.
In particular, the init specifiers for the comDriver instance
use the state value that we just mentioned.
13.4. Generation of Names
FPP uses the following rules to generate the names associated with
component instances.
First, as explained in the section on
specifying the implementation,
a component type M.C in FPP becomes the type M::C in C++.
Here C is a C++ class defined in namespace M that
implements the behavior of component C.
Second, a component instance I defined in module N becomes a C++ variable I defined in namespace N. For example, this FPP code
module N {
instance i: M.C base id 0x100
}becomes this code in the generated C++:
namespace N {
M::C i;
}So the fully qualified name of the instance is N.i in FPP and N::i
in C++.
Third, all other code related to instances is generated in the namespace of the
top-level implementation.
For example, in the System Reference example from the previous section,
the top-level implementation is in the namespace SystemReference, so
the code for configuring constants is generated in that namespace.
We will have more to say about the top-level implementation in
the section on implementing deployments.
Fourth, when generating the name of a constant associated with an instance,
FPP uses the fully-qualified name of the instance, and it replaces
the dots (in FPP) or the colons (in C++) with underscores.
For example, as discussed in the previous section, the configuration
constants for the instance SystemReference::cmdSeq are placed in
the namespace ConfigConstants::SystemReference_cmdSeq.
This namespace, in turn, is placed in the namespace SystemReference
according to the previous paragraph.
14. Defining Topologies
In F Prime, a topology or connection graph is the highest level of software architecture in a FSW application. A topology specifies what component instances are used in the application and how their port instances are connected.
An F Prime FSW application consists of a topology T; all the types, ports, and components used by T; and a small amount of top-level C++ code that you write by hand. In the section on implementing deployments, we will explain more about the top-level C++ code. In this section we explain how to define a topology in FPP.
14.1. A Simple Example
We begin with a simple example that shows how many of the pieces fit together.
port P
passive component C {
sync input port pIn: P
output port pOut: P
}
instance c1: C base id 0x100
instance c2: C base id 0x200
@ A simple topology
topology Simple {
@ This specifier says that instance c1 is part of the topology
instance c1
@ This specifier says that instance c2 is part of the topology
instance c2
@ This code specifies a connection graph C1
connections C1 {
c1.pOut -> c2.pIn
}
@ This code specifies a connection graph C2
connections C2 {
c2.pOut -> c1.pIn
}
}In this example, we define a port P.
Then we define a passive component C
with an input port and an output port, both of type P.
We define two instances of
C, c1 and c2.
We put these instances into a topology called Simple.
As shown, to define a topology, you write the keyword topology,
the name of the topology, and the members of the topology
definition enclosed in curly braces.
In this case, the topology has two kinds of members:
-
Two instance specifiers specifying that instances
c1andc2are part of the topology. -
Two graph specifiers that specify connection graphs named
C1andC2.
As shown, to write an instance specifier, you write the
keyword instance and the name of a component instance
definition.
In general the name may be a qualified name such as A.B.
if the instance is defined inside a
module; in this simple
example it is not.
Each instance specifier states that the instance it names
is part of the topology.
The instances appearing in the list must be distinct.
For example, this is not correct:
topology T {
instance c1
instance c1 # Error: duplicate instance c1
}A graph specifier specifies one or more connections between component instances. Each graph specifier has a name. By dividing the connections of a topology into named graphs, you can organize the connections in a meaningful way. For example you can have one graph group for connections that send commands, another one for connections that send telemetry, and so forth. We will have more to say about this in a later section.
As shown, to write a graph specifier, you may write the keyword connections
followed by the name of the graph; then you may list
the connections inside curly braces.
(In the next section, we will explain another way to write a graph specifier.)
Each connection consists of an endpoint, an arrow ->,
and another endpoint.
An endpoint is the name of a component instance
(which in general may be a qualified name), a dot,
and the name of a port of that component instance.
In this example there are two connection graphs, each containing one connection:
-
A connection graph
C1containing a connection fromc1.pOuttoc2.pIn. -
A connection graph
C2containing a connection fromc2.pOuttoc1.pIn.
As shown, topologies and their members are annotatable elements. The topology members form an element sequence in which the optional terminating punctuation is a semicolon.
14.2. Connection Graphs
In general, an FPP topology consists of a list of instances and a set of named connection graphs. There are two ways to specify connection graphs: direct graph specifiers and pattern graph specifiers.
14.2.1. Direct Graph Specifiers
A direct graph specifier provides a name and a list
of connections.
We illustrated direct graph specifiers in the
previous section, where the simple topology example
included direct graph specifiers for graphs named
C1 and C2.
Here are some more details about direct graph specifiers.
As shown in the previous section, each connection consists of an output port specifier, followed by an arrow, followed by an input port specifier. For example:
connections C {
a.p -> b.p
}Each of the two port specifiers consists of a component instance name, followed by a dot, followed the name of a port instance. The component instance name must refer to a component instance definition and may be qualified by a module name. For example:
connections C {
M.a.p -> N.b.p
}Here component instance a is defined in module M and component
instance b is defined in module N.
In a port specifier a.p, the port instance name p must refer to a
port instance of the
component definition associated with the component instance a.
Each component instance named in a connection must be part of the
instance list in the topology.
For example, if you write a connection a.b -> c.d inside
a topology T, and the specifier instance a does not
appear inside topology T, then you will get an error — even if a is a valid instance name for the FPP model.
The reason for this rule is that in flight code we need
to be very careful about which instances are included
in the application.
Naming all the instances also lets us check for
unconnected ports.
You may use the same name in more than one direct graph specifier in the same topology. If you do this, then all specifiers with the same name are combined into a single graph with that name. For example, this code
connections C {
a.p -> b.p
}
connections C {
c.p -> d.p
}is equivalent to this code:
connections C {
a.p -> b.p
c.p -> d.p
}The members of a direct graph specifier form an element sequence in which the optional terminating punctuation is a comma. For example, you can write this:
connections C { a.p -> b.p, c.p -> d.p }The connections appearing in direct graph specifiers must obey the following rules:
-
Each connection must go from an output port instance to an input port instance.
-
The types of the ports must match, except that a serial port instance may be connected to a port of any type. In particular, serial to serial connections are allowed.
-
If a typed port P is connected to a serial port in either direction, then the port type of P may not specify a return type.
14.2.2. Pattern Graph Specifiers
A few connection patterns are so common in F Prime that they
get special treatment in FPP.
For example, an F Prime topology typically includes an
instance of the component Svc.Time.
This component has a port timeGetPort
of type Fw.Time that other components can use to get the system
time.
Any component that gets the system time
(and there are usually several) has a connection to
the timeGetPort port of the Svc.Time instance.
Suppose you are constructing a topology in which
(1) sysTime is an instance of Svc.Time; and (2)
each of the instances
a, b, c, etc., has a
time get port
timeGetOut port connected to sysTime.timeGetPort,
If you used a direct graph specifier to write all these connections,
the result might look like this:
connections Time {
a.timeGetOut -> sysTime.timeGetPort
b.timeGetOut -> sysTime.timeGetPort
c.timeGetOut -> sysTime.timeGetPort
...
}This works, but it is tedious and repetitive. So FPP provides a better way: you can use a pattern graph specifier to specify this common pattern. You can write
time connections instance sysTimeThis code says the following:
-
Use the instance
sysTimeas the instance ofFw.Timefor the time connection pattern. -
Automatically construct a direct graph specifier named
Time. In this direct graph specifier, include one connection from each component instance that has a time get port to the input port ofsysTimeof typeFw.Time.
The result is as if you had written the direct graph specifier
yourself.
All the other rules for direct graph specifiers apply: for example,
if you write another direct graph specifier with name Time, then
the connections in that specifier are merged with the connections
generated by the pattern specifier.
In the example above, we call time the kind of the pattern
graph specifier.
We call sysTime the source instance of the pattern.
It is the source of all the time pattern connections
in the topology.
We call the instances that have time get ports (and so contribute
connections to the pattern) the target instances.
They are the instances targeted by the pattern once the source
instance is named.
Table Pattern Graph Specifiers shows the pattern graph specifiers allowed in FPP. The columns of the table have the following meanings:
-
Kind: The keyword or keywords denoting the kind. When writing the specifier, these appear just before the keyword
connections, as shown above for the time example. -
Source Instance: The source instance for the pattern.
-
Target Instances: The target instances for the pattern.
-
Graph Name: The name of the connection graph generated by the pattern.
-
Connections: The connections generated by the pattern.
The command pattern specifier generates three connection graphs:
Command, CommandRegistration, and CommandResponse.
| Kind | Source Instance | Target Instances | Graph Name | Connections |
|---|---|---|---|---|
|
All connections from the unique output port of type |
|||
|
An instance of |
Each instance that has command ports. |
|
All connections from the
|
|
All connections from the
|
|||
|
An instance of |
Each instance that has an
|
|
All connections from the
|
|
An instance of |
Each instance other than the source instance
that has a unique output port of type
|
|
(1) All connections from the unique output port of type
|
|
An instance of |
Each instance that has parameter ports. |
|
(1) All connections from the
|
|
An instance of |
Each instance that has a telemetry port. |
|
All connections from the
|
|
An instance of |
Each instance that has a |
|
All connections from the
|
|
An instance of |
Each instance that has a
|
|
All connections from the
|
Here are some rules for writing graph pattern specifiers:
-
At most one occurrence of each pattern kind is allowed in each topology.
-
For each pattern, the required ports shown in the table must exist and must be unambiguous. For example, if you write a time pattern
time connections instance sysTimethen you will get an error if
sysTimehas no input ports of typeFw.Time, You will also get an error ifsysTimehas two or more such ports.
The default behavior for a pattern is
to generate the connections for all target instances
as shown in the table.
If you wish, you may generate connections for a selected
set of target instances.
To do this, you write a list of target instances enclosed in
curly braces after the source instance.
For example, suppose a topology contains instances
a, b, and c each of which has an output port
that satisfies the time pattern.
And suppose that sysTime is an instance of Svc.Time.
Then if you write this pattern
time connections instance sysTimeyou will get a connection graph Time containing
time connections from each of a, b, and c to sysTime.
But if you write this pattern
time connections instance sysTime {
a
b
}then you will just get the connections from a and b
to sysTime.
The instances a and b must be valid target instances
for the pattern.
As with connections, you can write the instances a and b
each on its own line, or you can separate them with commas:
time connections instance sysTime { a, b }14.3. Port Numbering
As discussed in the section on defining components, each named port instance is actually an array of one or more port instances. When the size of the array exceeds one, you must specify the port number (i.e., the array index) of each connection going into or out of the port instance. In FPP, there are three ways to specify port numbers: explicit numbering, matched numbering, and general numbering.
14.3.1. Explicit Numbering
To use explicit numbering, you provide an explicit port number for a connection endpoint. You write the port number as a numeric expression in square brackets, immediately following the port name. The port numbers start at zero.
For example, the RateGroups graph of the Ref (reference) topology in the F Prime
repository defines the rate group connections.
It contains the following connection:
rateGroupDriverComp.CycleOut[Ports.RateGroups.rateGroup1] -> rateGroup1Comp.CycleIn
rateGroup1Comp.RateGroupMemberOut[0] -> SG1.schedIn
rateGroup1Comp.RateGroupMemberOut[1] -> SG2.schedIn
rateGroup1Comp.RateGroupMemberOut[2] -> chanTlm.Run
rateGroup1Comp.RateGroupMemberOut[3] -> fileDownlink.RunThe first line says to connect the port at index
Ports.RateGroups.rateGroup1 of rateGroupDriverComp.CycleOut
to rateGroup1Comp.CycleIn.
The symbol Ports.RateGroups.rateGroup1 is an enumerated constant, defined
like this:
module Ports {
enum RateGroups {
rateGroup1
rateGroup2
rateGroup3
}
}The second and following lines say to connect the ports of
rateGroup1Comp.RateGroupMemberOut at the indices 0, 1, 2, and 3
in the manner shown.
As another example, the Downlink graph of the reference topology
contains the following connection:
downlink.framedAllocate -> staticMemory.bufferAllocate[Ports.StaticMemory.downlink]This line says to connect downlink.framedAllocate to
staticMemory.bufferAllocate at index
Port.StaticMemory.downlink.
Again the port index is a symbolic constant.
If you wish, you may write two explicit port numbers, one at each endpoint. For example:
a.b[0] -> c.d[1]Here are some rules to keep in mind when using explicit numbering:
-
You can write any numeric expression as a port number. Each port number must be in bounds for the port (greater than or equal to zero and less than the size of the port array). If you write a port number that is out of bounds, you will get an error.
-
Use symbolic constants judiciously. Avoid scattering "magic" literal constants throughout the topology definition. For example:
-
The Ref topology uses the symbolic constants
Ports.RateGroups.rateGroup1andPorts.StaticMemory.downlink, as shown above. Because these constants appear in several different places, it is better to use symbolic constants here. Using literal constants would decrease readability and increase the chance of using incorrect or inconsistent numbers. -
The Ref topology uses the literal constants 0, 1, 2, and 3 to connect the ports of
rateGroup1Comp.RateGroupMemberOut. Here there are no obvious names to associate with the numbers, the numbers go in sequence, and all the numbers appear together in one place. So there is no clear benefit to giving them names.
-
-
Remember that in F Prime, multiple connections can go to the same input port, but only one connection can go from each output port. For example, this code is allowed:
c1.p1 -> c2.p[0] c1.p2 -> c2.p[0] # OK: Two connections into c2.p[0]But this code is incorrect:
c1.p[0] -> c2.p1 c1.p[0] -> c2.p2 # Error: Two connections out of c1.p[0] -
Use explicit numbering as little as possible. Instead, use matched numbering or general numbering (described in the next sections) and let FPP do the numbering for you. In particular, avoid writing zero indices such as
c.p[0]except in cases where you need to control the assignment of numbers, such as in the rate group example shown above. In other cases, writec.pand let FPP infer the zero index. For example, this is what we did in the section on direct graph specifiers.
14.3.2. Matched Numbering
Automatic matching: After resolving explicit numbering, the FPP translator applies matched numbering. In this step, the translator numbers all pairs of matched ports.
Matched numbering is essential for resolving the command and health patterns, each of which has matched ports. You can also use matched numbering in conjunction with direct graph specifiers. For example, the Ref topology contains the following connections:
connections Sequencer {
cmdSeq.comCmdOut -> cmdDisp.seqCmdBuff
cmdDisp.seqCmdStatus -> cmdSeq.cmdResponseIn
}
connections Uplink {
...
uplink.comOut -> cmdDisp.seqCmdBuff
cmdDisp.seqCmdStatus -> uplink.cmdResponseIn
...
}The port cmdDisp.seqCmdBuff port of the command dispatcher receives
command input from the command sequencer or from the ground.
The corresponding command response goes out on
port cmdDisp.seqCmdStatus.
These two ports are matched in the definition of the Command
Sequencer component.
When you use matched numbering with direct graph specifiers, you must obey the following rules:
-
When a component has the matching specifier
match p1 with p2, for every connection betweenp1and another component, there must be a corresponding connection between that other component andp2. -
You can use explicit numbering, and the automatic matching will work around the numbers you supply if it can. However, you may not do this in a way that makes the matching impossible. For example, you may not connect
p1[0]to another component andp2[1]to the same component, because this connection forces a mismatch. -
Duplicate connections at the same port number of
p1orp2are not allowed, even ifp1orp2are input ports.
If you violate these rules, you will get an error during analysis. You can relax these rules by writing unmatched connections, as described below.
Unmatched connections: Occasionally you may need to relax the rules for using matched ports. For example, you may need to match pairs of connections that use the F Prime hub pattern to cross a network boundary. In this case, although the connections are logically matched at the endpoints, they all go through a single hub instance on the side of the boundary that has the matched ports, and so they do not obey the simple rules for matching given here.
When a connection goes to or from a matched port,
we say that it is match constrained.
Ordinarily a match constrained connection must obey the
rules for matching stated above.
To relax the rules, you can write an unmatched connection.
To do this, write the keyword unmatched at the start of the connection
specifier.
Here is an example:
Port P
passive component Source {
sync input port pIn: [2] P
output port pOut: [2] P
match pOut with pIn
}
passive component Target {
sync input port pIn: [2] P
output port pOut: [2] P
}
instance source: Source base id 0x100
instance target: Target base id 0x200
topology T {
instance source
instance target
connections C {
unmatched source.pOut[0] -> target.pIn[0]
unmatched target.pOut[0] -> source.pIn[0]
unmatched source.pOut[1] -> target.pIn[1]
unmatched target.pOut[1] -> source.pIn[1]
}
}In this example, there are two pairs of connections between the
pIn and pOut connections of the instances source and target.
The ports of source are match constrained, so ordinarily
the connections would need to obey the matching rules.
The connections do partially obey the rules: for example,
there are no duplicate numbers, and the numbers match.
However, both pairs of connections go to and from the same
instance target; ordinarily this is not allowed for
match constrained connections.
To allow it, we need to use unmatched ports as shown.
Note the following about using unmatched ports:
-
When connections are marked
unmatched, the analyzer cannot check that the port numbers assigned to the connections conform to any particular pattern. If you need the port numbers to follow a pattern, as in the example shown above, then you must use explicit numbering. For a suggestion on how to do this, see the discussion of manual matching below. -
Unmatched ports must still obey the rule that distinct connections at a matched port must have distinct port numbers.
-
The
unmatchedkeyword is allowed only for connections that are match constrained, i.e., that go to or from a matched port. If you try to write an unmatched connection and the connection is not match constrained, then you will get an error.
Manual matching: Port matching specifiers work well when each matched pair of connections goes between the same two components, one of which has a matched pair of ports. If the matching does not follow this pattern, then automatic matched numbering will not work, and it is usually better not to use a port matching specifier at all. Instead, you can use explicit port numbers to express the matching. For example, the Ref topology contains these connections:
comm.allocate -> staticMemory.bufferAllocate[Ports.StaticMemory.uplink]
comm.$recv -> uplink.framedIn
uplink.framedDeallocate -> staticMemory.bufferDeallocate[Ports.StaticMemory.uplink]In this case the staticMemory instance requires that pairs of
allocation and deallocation requests for the same memory
go to the same port.
But the allocation request comes from comm,
and the deallocation request comes from uplink.
Since the allocation and deallocation connections go to different
component instances, we can’t used automatic matched numbering.
Instead we define a symbolic constant Ports.StaticMemory.uplink
and use that twice to do the matching by hand.
14.3.3. General Numbering
After resolving explicit numbering and matched numbering, the FPP translator applies general numbering. In this step, the translator uses the following algorithm to fill in any remaining unassigned port numbers:
-
Traverse the connections in a deterministic order. The order is fully described in The FPP Language Specification.
-
For each connection
-
If the output port number is unassigned, then set it to the lowest available port number.
-
If the input port number is unassigned, then set it to zero.
-
For example, consider the following connections:
a.p -> b.p
a.p -> c.pAfter general numbering, the connections could be numbered as follows:
a.p[0] -> b.p[0]
a.p[1] -> c.p[0]14.4. Importing Topologies
It is often useful to decompose a flight software project into several topologies. For example, a project might have the following topologies:
-
A topology for command and data handling (CDH) with components such as a command dispatcher, an event logger, a telemetry data base, a parameter database, and components for managing files.
-
Various subsystem topologies, for example power, thermal, attitude control, etc.
-
A release topology.
Each of the subsystem topologies might include the CDH topology. The release topology might include the CDH topology and each of the subsystem topologies. Further, to enable modular testing, it is useful for each topology to be able to run on its own.
In FPP, the way we accomplish these goals is to import one topology into another one. In this section of the User Guide, we explain how to do that.
14.4.1. Importing Instances and Connections
To import a topology A into a topology B, you write
import A inside topology B, like this:
topology B {
import A
...
}You may add instances and connections as usual to B, as shown
by the dots.
When you do this, the FPP translator does the following:
-
Resolve
A: Resolve all pattern graph specifiers inA, and resolve all explicit port numbers inA. Call the resulting topologyT. -
Form the instances of
B: Take the union of the instances specified inTand the instances specified inB, counting any duplicates once. These are the instances ofB. -
Form the connections of
B: Take the union of the connection graphs specified inTand the connection graphs specified inB. If each ofTandBhas a connection between the same ports, then each becomes a separate connection inB. -
Resolve
B: Resolve the pattern graph specifies ofB. Apply matched numbering and general numbering toB.
For example, suppose topologies A and B are defined
as follows:
topology A {
instance a
instance b
connections C1 {
a.p1 -> b.p
}
}
topology B {
import A
instance c
connections C1 {
a.p1 -> c.p
}
connections C2 {
a.p2 -> c.p
}
}After import resolution, B is equivalent to this topology:
topology B {
instance a
instance b
instance c
connections C1 {
a.p1 -> b.p
a.p1 -> c.p
}
connections C2 {
a.p2 -> c.p
}
}Notice that the C1 connections of A are merged with the C1
connections of B.
14.4.2. Private Instances
Often when importing topology A into topology B, you
want to include one or more instances in A that exist just
for running A, but that you don’t want imported into B.
For example, A could have an instance cStub which is a stub version of
a component c that is fully implemented in B.
In this case
-
When running
Ayou may needcStub; the topology may not run or may not even compile without it. -
When importing
AintoByou don’t want to importcStub, because it is superseded by the real implementationcinB. Also, any connections tocStubinAshould be replaced by connections tocinB.
To handle this case, you can make cStub a private instance
of A and c an instance of B.
When you import B into A, cStub will not become an instance
of B.
Further, no connections in A involving cStub will be imported
into B.
As an example, suppose we revise topology A from the previous
section as follows:
topology A {
instance a
instance b
private instance d
connections C1 {
a.p1 -> b.p
}
connections C2 {
a.p1 -> d.p
}
}Notice that we have added an instance d to topology
A, and we have declared d private to A.
We have also added a new connection to d in the
connection graph C2.
Now suppose that we use the same definition of B given
in the previous section.
After import resolution, B will still be equivalent
to the topology shown at the end of the last section:
we have added an instance and a connection to A,
but the instance is private and the connection goes
from a private instance, so neither the instance nor
the connection is imported into B.
14.4.3. Multiple Imports
Multiple imports are allowed. For example:
topology A {
import B
import C
...
}This has the obvious meaning: both topology B and
topology C are imported into topology A, according
to the rules described above.
Each topology may appear at most once in the import list. For example, this is incorrect:
topology A {
import B
import B # Error: B imported twice
}14.4.4. Transitive Imports
In general, transitive imports are allowed.
For example, topology A may import topology B,
and topology B may import topology C.
Resolution works bottom-up on the import graph:
for example, first we resolve C, and then we resolve B,
and then we resolve A.
Cycles in the import graph are not allowed.
For example, if A imports B and B imports C
and C imports A, you will get an error.
14.5. Include Specifiers
You can include code from another file in a topology definition.
You do this by writing an include specifier.
Here is a simple example, in which the body of a topology
definition is specified in a file T.fppi and then included
in a topology definition:
topology T {
include "T.fppi"
}We will explain more about this feature in the section on include specifiers below.
14.6. Telemetry Packets
When defining a topology, you may (but are not required to) specify how the telemetry channels defined in the topology are grouped into telemetry packets. If you do this, then you can use an F Prime component called the Telemetry Packetizer to construct telemetry packets and transmit them to the ground. This approach is usually more space efficient than transmitting individual channels. In this section we explain how to specify telemetry packets in FPP.
14.6.1. Telemetry Packet Sets
To group the channels of a topology T into packets, you write a telemetry packet set as part of the definition of T. Here is a simple example showing a complete topology with a telemetry packet set:
passive component C {
telemetry port tlmOut
time get port timeGetOut
telemetry T1: U32
telemetry T2: F32
}
instance c1: C base id 0x100
instance c2: C base id 0x200
topology T {
instance c1
instance c2
@ Telemetry packet set PacketSet
telemetry packets PacketSet {
@ Packet P1
packet P1 group 0 {
c1.T1
c2.T1
c1.T1
}
@ Packet P2
packet P2 group 1 {
c1.T2
c2.T2
}
}
}In this example, we have defined a passive component C with two telemetry
channels, T1 and T2.
We have defined two instances of C, c1 and c2, so that there
are four telemetry channels overall: c1.T1, c1.T2, c2.T1, and c2.T2.
We have defined a topology T that uses the instances c1 and c2
and defines a telemetry packet set PacketSet.
(In a realistic topology, there would be other instances and connections,
for example the telemetry packetizer instance and the ground interface
component. Here we have omitted these instances
and connections to focus on illustrating the FPP features.)
Notice the following about this example:
-
To write a telemetry packet set, you write the keywords
telemetrypacketsfollowed by the name of the packet set, herePacketSet. Then you write the body of the telemetry packet set inside curly braces{ … }. -
In the body of the packet set, you specify packets. The packet specifiers are annotatable elements. The body of the packet set is an element sequence in which the optional terminating punctuation is a comma.
-
Each packet specifier consists of the keyword
packet, the packet name, the keywordgroup, a group identifier, and the body of the packet. Within a telemetry packet set, the packet names must be distinct. The group identifiers must be numeric values. In particular they can be defined constants, enumerated constants, or arithmetic expressions. The Telemetry Packetizer uses the group identifiers to select which packets get transmitted. For example, it is possible to transmit packets from group 0 but not group 1. More than one packet may have the same group identifier. -
Inside each packet, you specify telemetry channels enclosed in curly braces
{ … }. The channel specifiers are annotatable elements. The body of the packet is an element sequence in which the optional terminating punctuation is a comma.
When the packets are serialized and transmitted, each packet with name
P contains data from
the channels listed in the specification for P, in the order that
the channels are specified.
As shown for packet P1, a single channel may appear more than
once in a packet; that means that data from that channel appears at
two or more offsets in that packet.
The form of a telemetry channel specifier
is an instance name followed by a dot and a channel name.
The instance name must refer to an instance of the topology.
The channel name must refer to a channel of that instance.
For example, in the model above, c1.T is a valid channel
for topology T because c1 is an instance of T,
c1 has type C, and T is a channel of C.
The instance name may be a qualified name containing a dot, as discussed in the section on defining modules. For example, if we had written
module M {
instance c1: C base id 0x100
}instead of
instance c1: C base id 0x100to define instance c1 in the model shown above,
then in the topology T we would write
instance M.c1 instead of instance c, and we would write
channel M.c1.T instead of channel c1.T.
14.6.2. Telemetry Packet Identifiers
Within a telemetry packet set, every packet has a unique numeric identifier. Typically the identifiers start at zero and count up by one. If you don’t specify an identifier, as in the example shown in the previous section, then FPP assigns a default identifier: zero for the first packet in the set; otherwise one more than the identifier of the previous packet.
If you wish, you may explicitly specify one or more packet identifiers. To do
this, you write the keyword id followed by a numeric expression immediately
after the packet name.
For example, in the model shown in the previous section, we
could have written
@ Packet P1
packet P1 id 0 group 0 {
c1.T1
c2.T1
c1.T1
}
@ Packet P2
packet P2 id 1 group 1 {
c1.T2
c2.T2
}for the packet specifiers, and this would have equivalent behavior.
14.6.3. Omitting Channels
By default, every telemetry channel in the topology must appear
in at least one telemetry packet.
For example, in the model shown above, if we comment out the definition
of packet P2 and run the result through fpp-check, then an error will result,
because neither channel
c1.T2 nor channel c2.T2 appears in any packet.
The purpose of this behavior is to ensure that you don’t omit
any channels from the telemetry by mistake.
If you do want to omit channels from the telemetry packets,
then you can do so explicitly by writing the keyword omit and listing
those channels after the main specification of the packet set.
Here is an example:
passive component C {
telemetry port tlmOut
time get port timeGetOut
telemetry T1: U32
telemetry T2: F32
}
instance c1: C base id 0x100
instance c2: C base id 0x200
topology T {
instance c1
instance c2
@ Telemetry packet set PacketSet
telemetry packets PacketSet {
@ Packet P1
packet P1 group 0 {
c1.T1
c2.T1
c1.T1
}
} omit {
c1.T2
c2.T2
}
}The form of the list of omitted channels is the same as the form of the list of channels in a telemetry packet. It is an error for any channel to appear in a telemetry packet and also to appear in the omitted list.
14.6.4. Specifying Multiple Telemetry Packet Sets
You may specify more than one telemetry packet set in a topology. Each telemetry packet set must have a distinct name. For example:
passive component C {
telemetry port tlmOut
time get port timeGetOut
telemetry T: U32
}
instance c1: C base id 0x100
instance c2: C base id 0x200
topology T {
instance c1
instance c2
@ Telemetry packet set PacketSet1
telemetry packets PacketSet1 {
@ Packet P
packet P1 group 0 {
c1.T
}
} omit {
c2.T
}
@ Telemetry packet set PacketSet2
telemetry packets PacketSet2 {
@ Packet P
packet P1 group 0 {
c2.T
}
} omit {
c1.T
}
}When you run the F Prime ground data system, you can tell it which telemetry packet set to use to decode the packets.
14.6.5. Include Specifiers
When writing a telemetry packet set, you can include code from another file in the following places:
-
You can include code inside a packet set specifier. The code must contain packet specifiers.
-
You can include code inside a packet specifier. The code must list telemetry channels.
For example:
telemetry packets PacketSet {
@ Include some packets
include "packets.fppi"
packet P group 0 {
c1.T1
# Include some channels
include "channels.fppi"
}
}The files that you include can themselves include code from other files, if you wish.
15. Specifying Models as Files
The previous sections have explained the syntactic and semantic elements of FPP models. This section takes a more file-centric view: it explains how to assemble a collection of elements specified in several files into a model.
We discuss several tools for specifying and analyzing dependencies between model files. We focus on how to use the tools, and we summarize their most important features. We do not attempt to cover every feature of every tool. For more comprehensive coverage, see the FPP wiki.
15.1. Dividing Models into Files
FPP does not require any particular division of model elements into files. For example, there is no requirement that each type definition reside in its own file. Nor is there any requirement that the names of files correspond to the names of the definitions they contain.
Of course you should try to adhere to good style when decomposing a large model into many files. For example:
-
Group related model elements into files, and name the files according to the purpose of the grouping.
-
Choose meaningful module names, and group all files in a single module in single directory (including its subdirectories). In the F Prime distribution, the
FwandSvcdirectories follow this pattern, where the C++ namespacesFwandSvccorrespond to FPP modules. -
Group files into modules and directories logically according to their function.
-
You can group files according to their role in the FPP model. For example, group types separately from ports.
-
You can group files according to their role in the FSW. For example, group framework files separately from application files.
-
-
If the definition of a constant or type is logically part of a component, then make the definition a member of the component.
There is still the usual requirement that a syntactic unit must begin and end in the same file. For example:
-
Each type definition is a syntactic unit, so each type definition must begin and end in the same file.
-
A module definition may span several syntactic units of the form
module { … }, so a module definition may span multiple files (with each unit of the formmodule { … }residing in a single file).
These rules are similar to the way that C++ requires a class definition
class C { … } or a namespace block namespace N { … } to reside in a
single file, but it allows the definition of a single namespace N to span
multiple blocks
namespace N { … } that can be in different files.
15.2. Include Specifiers
As part of an FPP model, you can write one or more include specifiers. An include specifier is an instruction to include FPP source elements from one file into another file. Include specifiers may occur at the top level of a model, inside a module definition, inside a state machine definition, inside a component definition, or inside a topology definition.
The main purpose of include specifiers is to split up large syntactic units into several files. For example, a component definition may include a telemetry dictionary from a separate file.
To write an include specifier, you write the keyword include
followed by string denoting a file path.
The path is relative to the file in which the include specifier appears.
By convention, included FPP files end in .fppi to distinguish
them from .fpp files that are directly analyzed and translated.
For example, suppose that the file a.fppi contains the definition
constant a = 0In a file b.fppi in the same directory, you could write this:
include "a.fppi"
constant b = aAfter resolving the include specifier, the model is equivalent to the following:
constant a = 0
constant b = aTo see this, do the following:
-
Create files
a.fppiandb.fppas described above. -
Run
fpp-format -i b.fpp.
fpp-format is a tool for formatting FPP source files.
It also can expand include specifiers.
fpp-format is discussed further in the section on
formatting FPP source.
As mentioned above, the path is relative to the directory
of the file containing the include specifier.
So if a.fppi is located in a subdirectory A, you could write this:
include "A/a.fppi"
constant b = aAnd if a.fppi is located in the parent directory, you could write this:
include "../a.fppi"
constant b = aYou can write an include specifier inside a module.
In this case, any definitions in the included file are treated as occurring
inside the module.
For example, if a.fppi contains the definition constant a = 0,
then this source text
module M { include "a.fppi" }defines the constant M.a.
As an exercise, try this:
% echo "module M { constant a = 0 }" > a.fppi
% fpp-check
include "a.fppi"
constant b = M.a
^D
%
The check should pass.
In any case, an included file must contain complete syntactic
units that may legally appear at the point where the include specifier appears.
For example, an included file may contain one or more constant
definitions or type definitions.
It may not contain a bare identifier a, as this is not a valid top-level
or module-level syntactic unit.
Nor is it valid to write an include specifier in a place where an identifier
like a
is expected.
For example, here is the result of a failed attempt to include an identifier into a constant definition:
% echo a > a.fppi
% fpp-check
module M { constant include "a.fppi" = 0 }
constant b = M.a
^D
fpp-check
stdin: 1.21
module M { constant include "a.fppi" = 0 }
^
error: identifier expected
%
15.3. Dependencies
Whenever a model spans two or more files, one file F may use one or more definitions appearing in other files. In order to analyze F, the tools must extract the definitions from these other files, called the dependencies of F.
For example, suppose the file a.fpp contains the following definition:
constant a = 0And suppose the file b.fpp contains the following definition:
constant b = aIf you present both files to fpp-check, like this:
% fpp-check a.fpp b.fpp
the check will pass.
However, if you present just b.fpp, like this:
% fpp-check b.fpp
you will get an error stating that the symbol a is undefined. (Try it and
see.)
The error occurs because the definition of a is located in a.fpp,
which was not included in the input to the analysis.
In this case we say that a.fpp is a dependency of b.fpp.
In order to analyze a file F (for example, b.fpp), the analyzer
needs to be told where to find all the dependencies of F (for example,
a.fpp).
For simple models, we can manage the dependencies by hand, as we did for the example above. However, for even moderately complex models, this kind of hand management becomes difficult. Therefore FPP has a set of tools and features for automatic dependency management.
In summary, dependency management in FPP works as follows:
-
You run a tool called
fpp-locate-defsto generate location specifiers for all the definitions that could be used in a set of files F. -
You run a tool called
fpp-depend, passing it the files F and the location specifiers generated in step 1. It emits a list of files containing definitions that are actually used in F (i.e., the dependencies of F).
These steps may occur in separate phases of development. For example:
-
You may run step 1 to locate all the type definitions available for use in the model.
-
You may run step 2 to develop ports that depend on the types. Typically you would run this step as part of a build process, e.g., the CMake build process included in the F Prime distribution.
Below we explain these steps in more detail.
15.4. Location Specifiers
A location specifier is a unit of syntax in an FPP model. It specifies the location of a definition used in the model.
Although it is possible to write location specifiers by hand, you should usually not do so. Instead, you should write definitions and let the tools discover their locations, as described in the section on locating definitions.
15.4.1. Syntax
In general, a location specifier consists of the keyword locate, a kind of
definition,
the name of a definition, and a string representing a file path.
For type and constant specifiers, there is also an optional dictionary
specifier, which we will describe
below.
For example, to locate the definition
constant a = 0appearing in the file a.fpp, we would write
# Locating a constant definition
locate constant a at "a.fpp"The kind of definition must be one of the following:
| Keyword | Meaning |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As a further example, to locate a type T in a file T.fpp, we would write the
following:
# Locating a type definition
locate type T at "T.fpp"To locate a port P in a file P.fpp, we write the following:
# Locating a port definition
locate port P at "P.fpp"To locate an enum, we locate the type; the location of the enumerated constants are then implied:
# Locating an enum definition,
# including the enumerated constant definitions
locate type E at "E.fpp"The other kinds operate similarly.
15.4.2. Path Names
As with
include specifiers,
the path name in a location specifier L is relative to the
location of the file where L appears.
For example, suppose the file b.fpp appears in the file system in some
directory D.
Suppose also that D has a subdirectory Constants, Constants contains a
file a.fpp,
and a.fpp defines the constant a.
Then in b.fpp we could write this:
locate constant a at "Constants/a.fpp"If, instead of residing in a subdirectory, a.fpp were located one directory above
b.fpp in the file system, we could write this:
locate constant a at "../a.fpp"15.4.3. Definition Names
The definition name appearing after the keyword locate
may be a qualified name.
For example, suppose the file M.fpp contains the following:
module M { constant a = 0 }Then in file b.fpp we could write this:
locate constant M.a at "M.fpp"Optionally, we may enclose the location specifier in the module M, like
this:
module M { locate constant a at "M.fpp" }A location specifier written inside a module this way has its definition name
implicitly qualified with the module name.
For example, the name a appearing in the example above is automatically
resolved to M.a.
Note that this rule is different than for other uses of definitions.
For example, when using the constant M.a in an expression inside module M,
you may spell the constant either a or M.a;
but when referring to the same constant M.a in a location specifier inside
module M, you must write a and not M.a.
(If you wrote M.a, it would be incorrectly resolved to M.M.a.)
The purpose of this rule is to facilitate dependency analysis,
which occurs before the analyzer has complete information about
definitions and their uses.
15.4.4. Included Files
When you write a file that contains definitions and you
include that file in another file,
the location of each definition is the file where the definition is
included, not the file where the definition appears.
For example, suppose that file a.fppi contains the
definition constant a = 0,
and suppose that file b.fpp contains the include specifier include "a.fppi".
When analyzing b.fpp, the location of the definition of the constant a
is b.fpp, not a.fppi.
15.4.5. Dictionary Definitions
For type and constant specifiers only, if the definition being located
is a
dictionary definition, then you must
write the keyword dictionary after the keyword locate
and before the definition kind.
For example, to locate the dictionary definition
dictionary constant b = 1appearing in the file b.fpp, we would write
# Locating a dictionary constant definition
locate dictionary constant b at "b.fpp"The dictionary keyword tells the analyzer that the definition is a dictionary
definition.
This fact is important when the model includes a topology definition.
In this case, the analyzer includes all dictionary definitions as
dependencies of the model.
That way the definitions are available
when generating the dictionary for the topology.
If a definition is a dictionary definition and the corresponding location
specifier does not specify dictionary (or vice versa), then the analyzer
will report an error.
15.4.6. Repeated Location Specifiers
An FPP model may contain any number of location specifiers for the same definition, so long as the following conditions are met:
-
All the specifiers must be consistent. This means that all the specifiers for the same definition provide the same location, and either they all specify
dictionaryor none of them does. -
All the specifiers must agree with the definition, if it exists in the model. This means that the location specifiers specify the location of the definition, and the specifiers specify
dictionaryif and only if the definition is a dictionary definition.
15.5. Locating Definitions
Given a collection of FPP source files F, you can generate location specifiers
for all the definitions in F.
The tool for doing this analysis is called fpp-locate-defs.
As example, you can run fpp-locate-defs to report the locations of all
the definitions in a subdirectory called Constants that contains constant
definitions for your model.
When analyzing other files that use the constants, you can use the location
specifiers to discover dependencies on individual files within Constants.
15.5.1. Running fpp-locate-defs
To locate definitions, do the following:
-
Collect all the FPP source files containing the definitions you want to locate. For example, run
find Constants -name '*.fpp'. -
Run
fpp-locate-defswith the result of step 1 as the command-line arguments. The result will be a list of location specifiers.
For example, suppose the file Constants/a.fpp defines the constant a.
Running
% fpp-locate-defs `find Constants -name '*.fpp'`
generates the location specifier
locate constant a at "Constants/a.fpp"15.5.2. Location Paths
By default, the location path is relative to the current
directory.
To specify a different base directory, use the option -d.
For example, running
% fpp-locate-defs -d Constants `find Constants -name '*.fpp'`
generates the location specifier
locate constant a at "a.fpp"15.5.3. Included Definitions
Consider the case where you write a definition in one file and
include that file in another file via an
include specifier.
For example, suppose file Constants.fpp looks like this:
module Constants {
constant a = 0
include "b.fppi"
}Suppose b.fppi contains the definition constant b = 1.
If you run find on this directory as described above and provide
the output to fpp-locate-defs, then you will get the following output:
-
The definition of constant
ais located atConstants.fpp. -
The definition of constant
bis also located atConstants.fpp.
For purposes of dependency analysis, this is what you want.
You want uses of b to depend on Constants.fpp (where the
definition
of b is included) rather than b.fpp (where the definition of b is
stated).
When running a find command to find files containing definitions,
you should exclude any files that are included in other files.
If your main FPP files end with .fpp and your included FPP files end with
.fppi, then running
find . -name '*.fpp'
will pick up just the main files.
15.6. Computing Dependencies
Given files F and location specifiers L that locate the definitions used in
F, you can
generate the dependencies of F.
The tool for doing this is called fpp-depend.
15.6.1. Running fpp-depend
To run fpp-depend, you pass it as input (1) files F that you want to
analyze
and (2) a superset of the location specifiers for the definitions used in that
code.
The tool extracts the location specifiers for the definitions used in F, resolves
them to absolute path names (the dependencies of F), and writes the
dependencies to standard output.
For example, suppose the file a.fpp contains the following
definition:
constant a = 0Suppose the file b.fpp contains the following definition:
constant b = 1Suppose the file locations.fpp contains the following location
specifiers:
locate constant a at "a.fpp"
locate constant b at "b.fpp"And suppose the file c.fpp contains the following definition of c,
which uses the definition of b but not the definition of a:
constant c = b + 1Then running fpp-depend locations.fpp c.fpp produces the output
[path-prefix]/b.fpp.
The dependency output contains absolute path names, which will vary from system
to system.
Here we represent the system-dependent part of the path as [path-prefix].
% fpp-depend locations.fpp c.fpp [path-prefix]/b.fpp
As usual with FPP tools, you can provide input as a set of files or on standard input. So the following is equivalent:
% cat locations.fpp c.fpp | fpp-depend [path-prefix]/b.fpp
15.6.2. Transitive Dependencies
fpp-depend computes dependencies transitively.
This means that if A depends on B and B
depends on C, then A depends on C.
For example, suppose again that locations.fpp
contains the following location specifiers:
locate constant a at "a.fpp"
locate constant b at "b.fpp"Suppose the file a.fpp contains the following definition:
constant a = 0Suppose the file b.fpp contains the following definition:
constant b = aAnd suppose that file c.fpp contains the following definition:
constant c = bNotice that there is a direct dependency of c.fpp on b.fpp
and a transitive dependency of c.fpp on a.fpp.
The transitive dependency occurs because there is a direct dependency
of c.fpp on b.fpp and a direct dependency of b.fpp on a.fpp.
Running fpp-depend on locations.fpp and c.fpp
produces both dependencies:
% fpp-depend locations.fpp c.fpp [path-prefix]/a.fpp [path-prefix]/b.fpp
15.6.3. Missing Dependencies
Suppose we construct the files locations.fpp and a.fpp, b.fpp, and c.fpp
as described in the previous section, but then we temporarily remove b.fpp.
Then the following facts are true:
-
fpp-dependcan see the direct dependency ofc.fpponb.fpp. -
fpp-dependcan see thatb.fppdoes not exist. In this case we say thatb.fppis a missing dependency. -
fpp-dependcannot see thatb.fppdepends ona.fpp(that dependency occurred in the missing file) and therefore it cannot see thatc.fppdepends ona.fpp.
In this case, by default, fpp-depend does the best that it can:
it reports the dependency of c.fpp on b.fpp.
% fpp-depend locations.fpp c.fpp [path-prefix]/b.fpp
The philosophy behind fpp-depend is to be as permissive and enabling as
possible.
It doesn’t assume that something is wrong because a dependency is missing:
for example, that dependency could be created later, as part of a code-generation
step.
However, you may want to know about missing dependencies, either to issue
a warning or error because something really is wrong, or to identify files to
generate.
To record missing dependencies, use the -m option.
It takes as an argument the name of a file, and it writes missing dependencies
(if any)
to that file.
For example, the command
fpp-depend -m missing.txt locations.fpp c.fpp
writes the missing dependency [path-prefix]/b.fpp to missing.txt in
addition to writing
the dependency [path-prefix]/b.fpp to standard output.
15.6.4. Included Files
Suppose file a.fpp contains the
include specifier
include "b.fppi".
Then there are two options for computing the dependencies of a.fpp:
-
a.fppdoes not depend onb.fppi. -
a.fppdoes depend onb.fppi.
Option 1 is what you want for assembling the input
to FPP analysis and translation tools such as fpp-check.
In this case, when analyzing a.fpp, the tool will resolve the include
specifier and include the contents of b.fppi. So b.fppi should
not be included as a separate input to the analysis.
On the other hand, suppose you are constructing a list of dependencies
for a build system such as the F Prime CMake system.
In this case, the build system doesn’t know anything about FPP include specifiers.
However, it needs to know that a.fpp does depend on b.fppi in the sense that
if b.fppi is modified, then a.fpp should be analyzed or translated again.
So in this case we want option 2.
By default, fpp-depend provides option 1:
% echo 'include "b.fppi"' > a.fpp % rm -f b.fppi % touch b.fppi % fpp-depend a.fpp
To get option 2, use the -i option to fpp-depend.
It takes as an argument the name of a file, and it writes the included dependencies
(if any) to that file.
% echo 'include "b.fppi"' > a.fpp % rm -f b.fppi % touch b.fppi % fpp-depend -i included.txt a.fpp % cat included.txt [path-prefix]/b.fppi
In practice, you usually run fpp-depend with the -i file option
enabled.
Then option 1 corresponds to the output of the tool, and option 2 corresponds
to the output plus the contents of file.
15.6.5. Dependencies Between Build Modules
As discussed
above, the standard output of fpp-depend reports transitive dependencies.
This is ordinarily what you want (a) for computing the input to an FPP
analysis tool and (b) for managing dependencies between files in a build.
For example, suppose that a.fpp depends on b.fpp and b.fpp depends on c.fpp.
When running analysis or code generation on a.fpp, you will need to import
b.fpp and c.fpp (see the
next section
for an example).
Further, if you have a build rule for translating a.fpp to C++, then you probably want to
re-run that rule if c.fpp changes.
Therefore you need to report a dependency of a.fpp on c.fpp.
However, suppose that your build system divides the FPP files into groups
of files called build modules, and it manages dependencies between
the modules.
This is how the F Prime CMake system works.
In this case, assuming there is no direct dependency from a.fpp to c.fpp,
you may not want to report a dependency from a.fpp to c.fpp
to the build system:
-
If
a.fppandc.fppare in the same build module, then they are in the same node of the dependency graph. So there is no dependency to manage. -
Otherwise, it suffices to report the file dependencies (a) from
a.fpptob.fppand (b) fromb.fpptoc.fpp. We can let the build system infer (a) the direct dependency from the module containinga.fppto the module containingb.fpp; (b) the direct dependency from the module containingb.fppto the module containingc.fpp; and (c) the transitive dependency from the module containinga.fppto the module containingc.fpp.
To compute direct dependencies, run fpp-depend with the option
-d file.
The tool will write a list of direct dependencies to file.
Because direct dependencies are build dependencies,
any
included files
will appear in the list.
For this purpose, an included file is (a) any file included by an
input file to fpp-depend; or (b) any file included
by such a file, and so forth.
When setting up a build based on build modules, you will typically
use fpp-depend as follows, for each module M in the build:
-
Let S be the list of source files in M.
-
Run
fpp-depend -m missing.txt -d direct.txtS and use the output as follows:-
The standard output reports the FPP source files to import when running FPP analysis tools on the module.
-
missing.txtreports missing dependencies. -
direct.txtreports direct dependencies. Use those to construct module dependencies for the build system.
-
You can also use the -g option to identify generated files;
we discuss this option
below.
Note that we do not use the -i option to fpp-depend, because the relevant
included files are already present in direct.txt.
15.6.6. Framework Dependencies
Certain FPP constructs imply dependencies on parts of the F Prime framework that may not be available on all platforms. For example, use of a guarded input port requires that an operating system provides a mutex lock.
To report framework dependencies, run fpp-depend with the option
-f file, where file is the name of an output file.
The currently recognized framework dependencies are as follows:
-
Fw_Compif the FPP model defines a passive component. -
Fw_CompQueuedif the model defines a queued or active component. -
Osif the model defines a queued or active component or uses a guarded input port specifier.
Each dependency corresponds to a build module (i.e., a
statically compiled library) of the F Prime framework.
fpp-depend writes the dependencies in the order that they must
be provided to the linker.
15.7. Locating Uses
Given a collection of files F and their dependencies D, you can generate the locations of the definitions appearing in D and used in F. This information is not necessary for doing analysis and translation — for that it is sufficient to know the file dependencies D. However, by reporting dependencies on individual definitions, this analysis provides an additional level of detail that may be helpful.
The tool for doing this analysis is called fpp-locate-uses.
As an example, you can run fpp-locate-uses to report the locations of all the
type definitions used in a port definition.
To locate uses, run fpp-locate-uses -i D F, where D is a comma-separated
list and F is a space-separated list.
The -i option stands for import: it says that the files D are to be read
for their
definitions, but not to be included in the results of the analysis.
For example, suppose a.fpp defines constant a, b.fpp defines constant
b,
and c.fpp uses a but not b.
Then fpp-locate-uses -i a.fpp,b.fpp c.fpp generates the output locate a at
"a.fpp"
Note that unlike in the case of
dependency analysis,
the inputs D and F to fpp-locate-uses must form a complete model.
There must be no name used in D or in F that is not defined somewhere in
D or in F.
If D is the output of running fpp-depend on F, and there are no
missing dependencies,
then this property should hold.
With fpp-locate-uses, you can automatically derive the equivalent of the
include
declarations that you would normally write by hand when programming in C++.
For example, suppose you have specified a port P that uses a type T.
To bring P into a C++ translation context, you would write an include
directive that
includes T into P. In FPP you don’t do this.
Instead, you can do the following:
-
Run
fpp-locate-defsto generate location specifiers L for all the type definitions. You can do this as needed, or you can do it once and check it in as part of the module that defines the types. -
Run
fpp-dependon L and P to generate the dependencies D of P. -
Run
fpp-locate-uses -iD P.
The result is a location specifier that gives the location of T. If you wish, you can check the result in as part of the source code that defines P. Doing this provide as a kind of “import statement,” if that is desired to make the dependencies explicit in the code. Or you can just use the procedure given above to generate the "import statement" whenever desired, and see the dependencies that way.
As with fpp-locate-defs, you can use -d to specify a base directory
for the location specifiers.
15.8. Path Name Aliases
Because FPP associates locations with symbols, and the locations are path names, care is required when using path names that are aliases of other path names, via symbolic links or hard links. There are two issues to consider: relative paths and unique locations.
15.8.1. Relative Paths and Symbolic Links
A relative path is a path that does not start with a slash and is relative to the current directory path, which is set by the environment in which an FPP tool is run. For example, the command sequence
% cd /home/user/dir
% fpp-check file.fppsets the current directory path to /home/user/dir and then runs
fpp-check file.fpp.
In this case, the relative path file.fpp is resolved to
/home/user/dir/file.fpp.
An absolute path is a path that starts with a slash and specifies
a complete path from the root of the file system, e.g.,
/home/user/dir/file.fpp.
Because FPP is implemented in Scala, relative paths are resolved by the Java Virtual Machine (JVM). When the current directory path contains a symbolic link, this resolution may not work in the way that you expect. For example, suppose the following:
-
D is an absolute path to a directory. D is a “real” path, i.e., none of the path elements in D is a symbolic link to a directory.
-
S is an absolute path in which one or more of the path elements is a symbolic link to a directory. After resolving all symbolic links, S points to D.
Suppose that D contains a file file.fpp, and that the
current directory path is D.
In this case, when you run an FPP tool with file.fpp as input,
any symbols defined in file.fpp will have location
D /file.fpp, as expected.
Now suppose that the current directory path is S.
In this case, when you run an FPP tool with file.fpp as input,
the symbols defined in file.fpp again have location D /file.fpp,
when you might expect them to have location S /file.fpp.
This is because the JVM resolves all symbolic links before computing
relative path names.
This behavior can cause problems when using the -p (path prefix)
option with FPP code generation tools, as described in the section on
analyzing and translating models.
See that section for details, and for suggested workarounds.
15.8.2. Unique Locations
The FPP analyzers assume that each symbol s has a unique path defining the location of the source file where s is defined. If paths contain names that are aliased via symbolic links or hard links, then this may not be true: for example, P1 and P2 may be syntactically different absolute paths that represent the same physical location in the file system. In this case it may be possible for the tools to associate two different locations with the same FPP symbol definition.
You must ensure that this doesn’t happen. If you present the same file F to the FPP tools several times, for example to locate definitions and to compute dependencies, you must ensure that the path describing F is the same each time, after resolving relative paths as described above.
16. Analyzing and Translating Models
The previous section explained how to specify an FPP model as a collection of files: how to divide a model into source files and how to compute the dependencies of one or more files on other files. This section explains the next step: how to perform analysis and translation on part or all of an FPP model, after specifying the model and computing its dependencies.
16.1. Checking Models
It is often useful to check a model for correctness, without
doing any translation.
The tool for checking models is called fpp-check.
If you provide one or more files as arguments, fpp-check
will attempt to read those files.
For example:
% fpp-check file1.fpp file2.fpp
If there are no arguments, then fpp-check reads from standard input.
For example:
% cat file1.fpp file2.fpp | fpp-check
If you run fpp-check with no arguments on the command line,
it will block and wait for standard input.
This is useful for interactive sessions, where you want
to type simple model text into the console and immediately check it.
fpp-check will keep reading input until (1) it encounters a parse error (more
on this below); or (2) you terminate the input with control-D (which must be
the first character in a line); or (3)
you terminate the program with control-C.
For larger models, the usual procedure for running fpp-check is as follows:
-
Identify one or more files F that you want to check.
-
Compute the dependencies D of F.
-
Run
fpp-checkD F.
All the files D and all the files F are specified as file arguments, separated by spaces.
When you run fpp-check, the following occurs:
-
The tool parses all the input files, recursively resolving include specifiers as it goes. If there are any parse errors or any problems resolving include files (for example, a missing file), it prints an error message to standard error and halts with nonzero status.
-
If parsing succeeds, then the tool runs semantic analysis. If everything checks out, the tool silently returns zero status. Otherwise it prints an error message to standard error and halts with nonzero status.
Checking for unconnected port instances: It is often useful to check for port instances that appear in a topology but that have no connections. For example, the following is a useful procedure for adding component instances and connections to a topology:
-
Add the component instances. In general this will introduce new port instances, which will initially be unconnected.
-
Check for unconnected port instances.
-
Add some or all of the connections identified in step 2.
-
Rerun steps 2 and 3 until there are no more missing connections, or you are certain that the missing connections are valid for your design.
To check for unconnected port instances (step 2 in the procedure above),
run fpp-check with the option -u file, where file is
the name of an output file.
fpp-check will write the names of all unconnected port instances
to the file.
For this purpose, a port instance array is considered unconnected
if none of its port numbers are connected.
For example:
% fpp-check -u unconnected.txt
port P
passive component C {
sync input port pIn: P
output port pOut: [2] P
}
instance c: C base id 0x100
topology T1 {
instance c
}
topology T2 {
instance c
connections C {
c.pOut -> c.pIn
}
}
^D
% cat unconnected.txt
Topology T1:
c.pIn
c.pOutIn this example, component instance c has the following port instances:
-
Two output port instances
c.pOut[0]andc.pOut[1]. -
One input port instance
c.pIn.
Topology T1 uses instance c and does not connect any port number of
c.pOut or c.pIn.
So the output written to unconnected.txt reports that fact.
On the other hand, in topology T2, both c.pOut and c.pIn
are considered connected (so not reported as unconnected)
even though c.Out has two ports and only one of them is connected.
16.2. Generating C Plus Plus
This section describes how to generate C++ from FPP.
Tool name: The tool for translating FPP to C++ is called
fpp-to-cpp.
Procedure:
The usual procedure for running fpp-to-cpp is as follows:
-
Identify one or more files F that you want to translate.
-
Compute the dependencies D of F.
-
If D is empty, then run
fpp-to-cppF. -
Otherwise run
fpp-to-cpp -iD1,…,Dn F, where Di are the names of the dependencies.
For example, suppose you want to generate C++ for the definitions in c.fpp,
If c.fpp has no dependencies, then run
% fpp-to-cpp c.fpp
On the other hand, if c.fpp depends on a.fpp and b.fpp, then run
% fpp-to-cpp -i a.fpp,b.fpp c.fpp
Notice that you provide the dependencies as a comma-separated list of
arguments to the option -i.
-i stands for import.
This option tells the tool that you want to read the files in D for their symbols,
but you don’t want to translate them.
Only the files F provided as arguments are translated.
Tool behavior: When you run fpp-to-cpp, the following occurs:
-
The tool runs the same analysis as for
fpp-check. If there is any problem, the tool prints an error message to standard error and halts with nonzero status. -
If the analysis succeeds, then the tool generates C++files, one for each definition appearing in F, with names as shown in the table above. The files are written to the current directory.
Standard input: Instead of providing named files as arguments,
you can provide FPP source on standard input, as described
for fpp-check.
C++ file names: The table C++ File Names shows how FPP definitions are translated to C++ files.
| FPP Definition | C++ Files |
|---|---|
Constants |
|
Array A outside any state machine or component |
A |
Array A in state machine M |
M |
Array A in component C |
C |
Enum E outside any state machine or component |
E |
Enum E in state machine M |
M |
Enum E in component C |
C |
State machine M outside any component |
M |
State machine M in component C |
C |
Struct S outside any state machine or component |
S |
Struct S in state machine M |
M |
Struct S in component C |
C |
Alias type A outside any state machine or component |
A |
Alias type A in state machine M |
M |
Alias type A in component C |
C |
Port P |
P |
Component C |
C |
Topology T |
T |
For example, consider the FPP array definition
array A = [3] U32Outside of any state machine or component definition,
this definition is translated to
a C++ class with name A defined in a files AArrayAc.hpp
and AArray.cpp.
Inside the definition of a component C, it is translated to
a class with name C_A defined in the files C_AArrayAc.hpp
and C_AArray.cpp.
Inside the definition of a state machine M, it is translated to
a class with name M_A defined in the files M_AArrayAc.hpp
and M_AArray.cpp.
In any case, the C++ namespace is given by the enclosing
FPP modules, if any.
For example, the following code
module M {
array A = [3] U32
}generates an array class M::A in files AArrayAc.hpp
and AArrayAc.cpp.
Headers for alias types:
For alias types, a C++ header with suffix .hpp is always generated.
A C header with suffix .h is also generated if the alias type
is C-compatible.
This means (1) the underlying
type is a signed or unsigned integer type or a floating-point type,
and (2) the alias type definition does not appear in an FPP module
or component, and (3) if the alias type refers to another alias
type T, then T is C-compatible.
For example, the following alias types are C-compatible
and cause .h headers to be generated:
type T1 = U32
type T2 = T1The following alias types are not C-compatible, so
they do not cause .h headers to be generated:
module M {
type T1 = U32 # Definition is in a module
}
type T2 = M.T1 # M.T1 is not C-compatible
array A = [3] U32
type T3 = A # A is not C-compatibleWhen both headers are generated, you should include the .h header in your
C programs and the .hpp header in your C++ programs.
16.2.1. Constant Definitions
fpp-to-cpp extracts constant definitions
from the source files F.
It generates files FppConstantsAc.hpp and FppConstantsAc.cpp
containing C++ translations of the constants.
By including and/or linking against these files,
you can use constants defined in the FPP model
in your FSW implementation code.
To keep things simple, only numeric, string, and Boolean constants are translated; struct and array constants are ignored. For example, the following constant is not translated, because it is an array:
constant a = [ 1, 2, 3 ]To translate array constants, you must expand them to values that are translated, like this:
constant a0 = 1
constant a1 = 2
constant a2 = 3
constant a = [ a0, a1, a2 ]Constants are translated as follows:
-
Integer constants become enumeration constants.
-
Floating-point constants become
constfloating-point variables. -
boolpoint constants becomeconst boolvariables. -
stringconstants becomeconst char* constvariables initialized with string literals.
As an example, try this:
% fpp-to-cpp @ Constant a constant a = 1 @ Constant b constant b = 2.0 @ Constant c constant c = true @ Constant d constant d = "abcd" ^D
You should see files FppConstantsAc.hpp and FppConstantsAc.cpp
in the current directory.
Examine them to confirm your understanding of how the translation
works.
Notice how the FPP annotations are translated to comments.
(We also remarked on this in the section on
writing annotations.)
Constants defined inside state machines:
As noted in the section on
defining state machines,
when you define a constant c inside a state machine M,
the name of the corresponding constant in the generated C++
code is M_c.
As an example, run the following code through fpp-to-cpp
and examine the results:
state machine M {
constant c = 0
state S
initial enter S
}Constants defined inside components:
As noted in the section on
defining components,
when you define a constant c inside a component C,
the name of the corresponding constant in the generated C++
code is C_c.
As an example, run the following code through fpp-to-cpp
and examine the results:
passive component C {
constant c = 0
}Generated header paths:
When one FPP definition A refers to another definition B,
the generated C++ file for A contains a directive to
include the generated header file for B.
The tool constructs the import path from the
location of the
definition of B.
For example, suppose the file [path prefix]/A/A.fpp contains the following
definition, where [path prefix] represents the path prefix of directory
A starting from the root of the file system:
array A = [3] BAnd suppose the file [path prefix]/B/B.fpp contains the following definition:
array B = [3] U32If you run this command in directory [path prefix]/A
% fpp-to-cpp -i ../B/B.fpp A.fpp
then in that directory the tool will generate a file AArrayAc.hpp containing
the following line:
#include "[path prefix]/B/BArrayAc.hpp"Removing path prefixes: Usually when generating C++ we don’t want to include the system-specific path prefix. Instead, we want the path to be specified relative to some known place, for example the root of the F Prime repository or a project repository.
To remove the prefix prefix from generated paths, use the option
-p prefix .
To continue the previous example, running
fpp-to-cpp -i ../B/B.fpp -p [path prefix] A.fpp
generates a file AArrayAc.hpp containing the line
#include "B/BArrayAc.hpp"Notice that the path prefix [path prefix]/ has been removed.
To specify multiple prefixes, separate them with commas:
fpp-to-cpp -p prefix1,prefix2, ...
For each generated path, the tool will delete the longest prefix that matches a prefix in the list.
As discussed in the section on
relative paths and symbolic links,
when a file name is relative to a path S that includes symbolic links,
the associated location is relative to the directory D pointed to by S.
In this case, providing S as an argument to -p will not work as expected.
To work around this issue, you can do one of the following:
-
Provide both D and S as arguments to
-p. -
Use absolute paths when presenting files to FPP code generation tools with the
-poption.
The include guard prefix: By default, the include guard
for FppConstantsAc.hpp is guard-prefix _FppConstantsAc_HPP,
where guard-prefix is the absolute path of the current
directory, after replacing non-identifier characters with underscores.
For example, if the current directory is /home/user, then
the guard prefix is _home_user, and the include guard is
_home_user_FppConstantsAc_HPP.
The -p option, if present, is applied to the guard
prefix.
For example, if you run fpp-to-cpp -p $PWD … then
the guard prefix will be empty.
In this case, the guard is FppConstantsAc_HPP.
If you wish to use a different prefix entirely, use the option
-g guard-prefix.
For example, if you run fpp-to-cpp -g Commands …,
then the include guard will be Commands_FppConstantsAc_HPP.
More options: The following additional options are available
when running fpp-to-cpp:
-
-ddir : Use dir instead of the current directory as the output directory for writing files. For example,fpp-to-cpp -d cpp ...
writes output files to the directory
cpp(which must already exist). -
-nfile : Write the names of the generated C++ files to file. This is useful for collecting autocoder build dependencies.
16.2.2. Types, Ports, State Machines, and Components
Generating code:
To generate code for type, port, state machine, and component definitions, you
run fpp-to-cpp in the same way as for
constant definitions, with one exception:
the translator ignores the -g option, because the include guard comes from
the qualified name of the definition.
For example, a component whose qualified name in FPP is A.B.C
uses the name A_B_CComponentAc_HPP in its include guard.
Alias types:
The generated code for an alias type
definition is either a C-style typedef (in a .h file) or a C++11-style
using alias (in a .hpp file). The generated code for an alias to an FPP
string type is always an alias to the F Prime type Fw::String; the size in
the string type is ignored when generating the alias.
For example, the following alias type definitions
all generate aliases to Fw::String, either directly or indirectly:
type FwSizeStoreType = U16
type T1 = string size 40 # Generates an alias to Fw::String
type T2 = string size 80 # Generates an alias to Fw::String
type T3 = T2 # Generates an alias to T2, which is an alias to Fw::StringWhen reporting generated files for alias types via the -n option,
fpp-to-cpp reports only .hpp files, not .h files.
This is to keep the analysis simple, so that it can be run when
computing dependencies.
In a future version of FPP, we may revise the analysis strategy
and report the generation of .h files as well.
Using the generated code: Once you generate C++ code for these definitions, you can use it to write a flight software implementation. The F User Manual explains how to do this.
For more information about the generated code for data products, for state machines, and for state machine instances, see the F Prime design documentation.
16.2.3. Component Implementation and Unit Test Code
fpp-to-cpp has options -t and -u for generating component “templates”
or
partial implementations and for generating unit test code.
Here we cover the mechanics of using these options.
For more information on implementing and testing components in F Prime, see
the F Prime User Manual.
Generating implementation templates:
When you run fpp-to-cpp with option -t and without option -u,
it generates a partial implementation for
each component definition C in the input.
The generated files are called C .template.hpp and C .template.cpp.
You can fill in the blanks in these files to provide the concrete
implementation of C.
Generating unit test harness code:
When you run fpp-to-cpp with option -u and without option -t,
it generates support code for testing each component definition C
in the input.
The unit test support code resides in the following files:
-
C
TesterBase.hppand CTesterBase.cpp. These files define a class CTesterBase. This class contains helper code for unit testing C, for example an input port and history corresponding to each output port of C. -
C
GTestBase.hppand CGTestBase.cpp. These files define a class CGTestBasederived from C. This class uses the Google Test framework to provide additional helper code. It is factored into a separate class so that you can use CTesterBasewithout CGTestBaseif you wish.
Generating unit test templates:
When you run fpp-to-cpp with both the -u and the -t options,
it generates a template or partial implementation of the unit tests
for each component C in the input.
The generated code consists of the following files:
-
C
Tester.hppand CTester.cpp. These files partially define a class CTesterthat is derived from CGTestBase. You can fill in the partial definition to provide unit tests for C. If you are not using Google Test, then you can modify CTesterso that it is derived from CTesterBase. -
C
TesterHelpers.cpp. This file provides helper functions called by the functions defined inTester.cpp. These functions are factored into a separate file so that you can redefine them if you wish. To redefine them, omit CTesterHelpers.cppfrom your F Prime unit test build. -
C
TestMain.cpp. This file provides a minimal main function for unit testing, including a sample test. You can add your top-level test code to this file.
Unit test auto helpers:
When running fpp-to-cpp with the -u option, you can also specify the -a
or unit test auto helpers option.
This option moves the generation of the file C TesterHelpers.cpp
from the unit test template code to the unit test harness code.
Specifically:
-
When you run
fpp-to-cpp -a -u, the file CTesterHelpers.cppis generated. -
When you run
fpp-to-cpp -a -t -u, the file CTesterHelpers.cppis not generated.
The -a option supports a feature of the F Prime CMake build system called
UT_AUTO_HELPERS. With this feature enabled, you don’t have to manage the
file C TesterHelpers.cpp as part of your unit test source files; the
build system does it for you.
16.2.4. Topology Definitions
fpp-to-cpp also extracts topology definitions
from the source files.
For each topology T defined in the source files, fpp-to-cpp
writes files T TopologyAc.hpp and T TopologyAc.cpp.
These files define two public functions:
setup for setting up the topology, and
teardown, for tearing down the topology.
The function definitions come from the definition of T and
from the
init specifiers
for the component instances used in T.
You can call these functions from a handwritten main
function.
We will explain how to write this main function in the
section on
implementing deployments.
As an example, you can do the following:
-
On the command line, run
fpp-to-cpp -p $PWD. -
Copy the text of the simple topology example and paste it into the terminal.
-
Press return, control-D, and return.
-
Examine the generated files
SimpleTopologyAc.hppandSimpleTopologyAc.cpp.
You can examine the files RefTopologyAc.hpp and RefTopologyAc.cpp
in the F Prime repository.
Currently these files are checked in at Ref/Top.
Once we have integrated FPP with CMake, these files will be auto-generated
by CMake and will be located at Ref/build-fprime-automatic-native/F-Prime/Ref/Top.
Options:
When translating topologies,
the -d, -n, and -p options work in the same way as for
translating constant definitions.
The -g option is ignored, because
the include guard prefix comes from the name of the topology.
16.2.5. Compiling the Generated Code
The generated C++ is intended to compile with the following gcc and clang compiler flags:
--std=c++11 -Wall -Wconversion -Wdouble-promotion -Werror -Wextra -Wno-unused-parameter -Wold-style-cast -Wshadow -pedantic
When using clang, the following flags must also be set:
-Wno-vla-extension
16.3. Formatting FPP Source
The tool fpp-format accepts FPP source files as input
and rewrites them as formatted output.
You can use this tool to put your source files into
a standard form.
For example, try this:
% fpp-format
array A = [3] U32 default [ 1, 2, 3 ]
^D
array A = [3] U32 default [
1
2
3
]
fpp-format has reformatted the default value so that each array
element is on its own line.
By default, fpp-format does not resolve include specifiers.
For example:
% echo 'constant a = 0' > a.fppi % fpp-format include "a.fppi" ^D include "a.fppi"
The -i option causes fpp-format to resolve include specifiers.
For example:
% echo 'constant a = 0' > a.fpp % fpp-format -i include "a.fppi" ^D constant a = 0
fpp-format has one big limitation: it goes through
the FPP parser, so it deletes all
comments
from the program
(annotations
are preserved).
To preserve comments on their own lines that precede
annotatable elements, you can run this script:
#!/bin/sh
sed 's/^\( *\)#/\1@ #/' | fpp-format $@ | sed 's/^\( *\)@ #/\1#/'It converts comments to annotations, runs fpp-format, and converts the
annotations back to comments.
16.4. Visualizing Topologies
FPP provides a tool called fpp-to-layout for generating files
that you can use to visualize topologies.
Given a topology T, this tool generates a directory containing
the layout input files for T.
There is one file for each connection
graph in T.
The files are designed to work with a tool called fprime-layout, which
we describe below.
Procedure:
The usual procedure for running fpp-to-layout is as follows:
-
Identify one or more files F containing topology definitions for which you wish to generate layout input files.
-
Compute the dependencies D of F.
-
If D is empty, then run
fpp-to-layoutF. -
Otherwise run
fpp-to-layout -iD1,…,Dn F, where Di are the names of the dependencies.
Except for the tool name, this procedure is identical to the one given for generating C++.
Input: You can provide input to fpp-to-layout
either through named files or through standard input.
Tool behavior:
For each topology T defined in the input files F, fpp-to-layout does
the following:
-
If a directory named T
Layoutexists in the current directory, then remove it. -
Create a directory named T
Layoutin the current directory. -
In the directory created in step 2, write one layout input file for each of the connection graphs in T. The
fprime-layoutwiki describes the file format.
Options:
fpp-to-layout provides an option -d for selecting the current directory
to use when writing layout input files.
This option works in the same way as for
fpp-to-cpp.
See the FPP wiki for details.
Producing visualizations:
Once you have generated layout input files, you can use a
companion tool called fprime-layout to read the files and produce a
topology visualization, i.e., a graphical rendering of the topology in which
the component instances are shapes, the ports are smaller shapes, and the
connections are arrows between the ports.
Topology visualization is an important part of the FPP work flow:
-
It provides a graphical representation of the instances and connections in each connection graph. This graphical representation is a useful complement to the textual representation provided by the FPP source.
-
It makes explicit information that is only implicit in the FPP source, e.g., the auto-generated port numbers of the connections and the auto-generated connections of the pattern graph specifiers.
Using fprime-layout, you can do the following:
-
Render the connection graphs as EPS (Encapsulated PostScript), generating one EPS file for each connection graph.
-
Generate a set of layouts, one for each layout input file, and view the layouts in a browser.
See the fprime-layout
repository for more details.
16.5. Generating Ground Dictionaries
A ground dictionary specifies all the commands, events, telemetry, parameters, and data products in a FSW application. Typically a ground data system (GDS), such as the F Prime GDS, uses the ground dictionary to provide the operational interface to the application. The interface typically includes real-time commanding; real-time display of events and telemetry; logging of commands, events, and telemetry; uplink and downlink of files, including data products; and decoding of data products. This section explains how to generate ground dictionaries from FPP models.
Tool name: The tool for generating ground dictionaries is called
fpp-to-dict.
Procedure:
The usual procedure for running fpp-to-dict is as follows:
-
Identify one or more files F that you want to translate.
-
Compute the dependencies D of F.
-
If D is empty, then run
fpp-to-dictF. -
Otherwise run
fpp-to-dict -iD1,…,Dn F, where Di are the names of the dependencies.
Except for the tool name, this procedure is identical to the one given for generating C++.
Input: As with the tools described above, you can provide input to
fpp-to-dict
either through named files or through standard input.
Tool behavior:
For each topology T defined in the input files F, fpp-to-dict writes a
file
T TopologyDictionary.json.
The dictionary is specified in JavaScript Object Notation (JSON) format.
The JSON format is specified in the
F Prime design
documentation.
Here is a common use case:
-
The input files F define a single topology T. T describes all the component instances and connections in a FSW application, and the generated dictionary T
TopologyDictionary.jsonis the dictionary for the application. -
If T imports subtopologies, then those subtopologies are defined in the dependency files D. That way the subtopologies are part of the model, but no dictionaries are generated for them.
F Prime configuration:
When you run fpp-to-dict on an FPP model, the model must provide the
framework constants
and
framework types
specified in the
F Prime
dictionary specification.
These types and constants are required by the F Prime GDS, so they are included
in the dictionary.
Typically you specify these types and constants as part of F Prime
configuration, in files named FpConfig.fpp and FpConstants.fpp.
See the
F
Prime documentation for details.
Options:
fpp-to-dict provides the following options:
-
The
-doption works in the same way as forfpp-to-cpp. -
You can use the
-fand-poptions to specify a framework version and project version for the dictionary. That way the dictionary is stamped with information that connects it to the FSW version for which it is intended to be used. -
You can use the
-loption to specify library versions used in the project.
See the FPP wiki for details.
16.6. Identifying Generated Files
As discussed in the
section on generating
C++,
the -n option
of fpp-to-cpp lets you collect the names of
files generated from an FPP model as those files are generated.
However, sometimes you need to know the names of the generated
files up front.
For example, the CMake build tool writes out a Makefile rule
for every generated file, and it does this as an initial step
before generating any files.
There are two ways to collect the names of generated files:
using fpp-filenames and using fpp-depend.
16.6.1. Using fpp-filenames
Like fpp-check, fpp-filenames reads the files
provided as command-line arguments if there are any;
otherwise it reads from standard input.
The FPP source presented to fpp-filenames need not be a complete
model (i.e., it may contain undefined symbols).
When run with no options, tool parses the FPP source that you give it.
It identifies all definitions in the source that would cause
C++ files to be generated when running
fpp-to-cpp or fpp-to-dict.
Then it writes the names of those files to standard output.
For example:
% fpp-filenames array A = [3] U32 ^D AArrayAc.cpp AArrayAc.hpp
% fpp-filenames constant a = 0 ^D FppConstantsAc.cpp FppConstantsAc.hpp
You can run fpp-filenames with the -u option, with the -t option,
or with both options.
In these cases fpp-filenames writes out the names of
the files that would be generated by running fpp-to-cpp with the
corresponding options.
For example:
% fpp-filenames -t
array A = [3] U32
passive component C {}
^D
C.template.cpp
C.template.hpp
% fpp-filenames -u
array A = [3] U32
passive component C {}
^D
array A = [3] U32
passive component C {}
AArrayAc.cpp
AArrayAc.hpp
CComponentAc.cpp
CComponentAc.hpp
CGTestBase.cpp
CGTestBase.hpp
CTesterBase.cpp
CTesterBase.hpp
% fpp-filenames -u -t
array A = [3] U32
passive component C {}
^D
CTestMain.cpp
CTester.cpp
CTester.hpp
CTesterHelpers.cpp
You can also also run fpp-filenames with the -a option.
Again the results correspond to running fpp-to-cpp with this option.
For example:
% fpp-filenames -a -u -t
array A = [3] U32
passive component C {}
^D
CTestMain.cpp
CTester.cpp
CTester.hpp
16.6.2. Using fpp-depend
Alternatively, you can use
fpp-depend
to write out the names of generated files during dependency analysis.
The output is the same as for fpp-filenames, but this way you can
run one tool (fpp-depend) instead of two (fpp-depend and
fpp-filenames).
Running one tool may help your build go faster.
To write out the names of generated files, you can use the following
options provided by fpp-depend:
-a: Report the generation of files with
unit
test auto helpers enabled.
-g file: Write the names of the generated autocode files
to the file file.
-u file: Write the names of the unit test support code
files to file.
For example:
% fpp-depend -g generated.txt -u ut-generated.txt
array A = [3] U32
passive component C {}
^D
% cat generated.txt
AArrayAc.cpp
AArrayAc.hpp
CComponentAc.cpp
CComponentAc.hpp
% cat ut-generated.txt
CGTestBase.cpp
CGTestBase.hpp
CTesterBase.cpp
CTesterBase.hpp
% fpp-depend -a -g generated.txt -u ut-generated.txt
array A = [3] U32
passive component C {}
^D
% cat generated.txt
AArrayAc.cpp
AArrayAc.hpp
CComponentAc.cpp
CComponentAc.hpp
% cat ut-generated.txt
CGTestBase.cpp
CGTestBase.hpp
CTesterBase.cpp
CTesterBase.hpp
CTesterHelpers.cpp
fpp-depend does not have an option for writing out the names of
implementation template files, since those file names are not
needed during dependency analysis.
16.7. Generating JSON Models
FPP provides a tool called fpp-to-json for converting FPP models to
JavaScript Object Notation (JSON) format.
Using this tool, you can import FPP models into programs written
in any language that has a library for reading JSON, e.g., JavaScript,
TypeScript, or Python.
Generating and importing JSON may be convenient if you need to develop
a simple analysis or translation tool for FPP models, and you don’t
want to develop the tool in Scala.
For more complex tools, we recommend that you develop in Scala
against the FPP compiler data structures.
Procedure:
The usual procedure for running fpp-to-json is as follows:
-
Identify one or more files F that you want to analyze.
-
Compute the dependencies D of F.
-
Run
fpp-to-jsonD F. Note that D may be empty.
If you are using fpp-to-json with the -s option (see below),
then you can run fpp-to-json F, without computing dependencies.
Tool behavior: When you run fpp-to-json, the tool checks the
syntax and semantics of the source model, reporting any errors that occur.
If everything checks out, it generates three files:
-
fpp-ast.json: The abstract syntax tree (AST). This is a tree data structure that represents the source syntax. It contains AST nodes, each of which has a unique identifier. -
fpp-loc-map.json: The location map. This object is a map from AST node IDs to the source locations (file, line number, and column number) of the corresponding AST nodes. -
fpp-analysis.json: The Analysis data structure. This object contains semantic information inferred from the source model, e.g., the types of all the expressions and the constant values of all the numeric expressions. Only output data is included in the JSON; temporary data structures used during the analysis algorithm are omitted. For more information on the Analysis data structure, see the FPP wiki.
JSON format: To understand this subsection, you need to know a little bit about case classes in Scala. For a primer, see this wiki page.
The JSON translation uses a Scala library called Circe. In general the translation follows a set of standard rules, so the output format can be easily inferred from the types of the data structures in the FPP source code:
-
A Scala case class
Cis translated as follows, unless it extends a sealed trait (see below). A valuevof typeCbecomes a JSON dictionary with the field names as keys and the field values as their values. For example a valueC(1,"hello")of typecase class C(n: Int, s: String)becomes a JSON value{ "n": 1, "s": "String" }. -
A Scala case class
Cthat extends a sealed traitTrepresents a named variant of typeT. In this case a valuevof typeCis wrapped in a dictionary with one key (the variant nameC) and one value (the valuev). For example, a valueC(1)of typecase class C(n: Int) extends Tbecomes a JSON value{ "C" : { "n" : 1 } }, while a valueD("hello")of typecase class D(s: String) extends Tbecomes a JSON value{ "D" : { "s" : "hello" } }. In this way each variant is labeled with the variant name. -
A Scala list becomes a JSON array, and a Scala map becomes a JSON dictionary.
There are a few exceptions, either because the standard translation does not work, or because we need special behavior for important cases:
-
We streamline the translation of the Scala Option type, translating
Some(v)as{ "Some" : v }andNoneas"None". -
In the AST, we translate the type AstNode as if it were a variant type, i.e., we translate
AstNode([data], [id])to"AstNode" : { "data" : [data], "id" : [id] } }. TheAstNodekeys identify the AstNode objects. -
In the AST, to reduce clutter we skip over the
nodefield of module, component, and topology member lists. This field is an artifact of the way the Scala code is written; deleting it does not lose information. -
In the Analysis data structure, to avoid repetition, we translate AstNode values as
{ "astNodeId" : [node id] }, eliminating the data field of the node. We also omit annotations from annotated AST nodes. The data fields and the annotations can be looked up in the AST, by searching for the node ID. -
When translating an FPP symbol (i.e., a reference to a definition), we provide the information in the Symbol trait (the node ID and the unqualified name). All symbols extend this trait. We omit the AST node information stored in the concrete symbol. This information can be looked up with the AST node ID.
-
When translating a component instance value, we replace the component stored in the value with the corresponding AST node ID.
-
When the keys of a Scala map cannot easily be converted to strings, we convert the map to a list of pairs, represented as an array of JSON arrays. For example, this is how we translate the PortNumberMap in the Analysis data structure, which maps Connection objects to integers.
Options: The following options are available
when running fpp-to-json:
-
-ddir : Similar to the corresponding option offpp-to-cpp. -
-s: Analyze syntax only: With this option,fpp-to-jsongenerates the AST and the location map only; it doesn’t generate the Analysis data structure. Because semantic analysis is not run, you don’t have to present a complete or semantically correct FPP model to the tool.
16.8. Translating Older XML to FPP
Previous versions of F Prime used XML to represent model elements such as components and ports. The FPP tool suite provides a capability to translate this older format to FPP. Its purpose is to address the following case:
-
You have an older F Prime model that was developed in XML.
-
You wish to translate the model to FPP in order to use FPP as the source language going forward.
The XML-to-FPP translation is designed to do most of the work in translating an XML model into FPP. As discussed below, some manual effort will still be required, because the FPP and XML representations are not identical. The good news is that this is a one-time effort: you can do it once and use the FPP version thereafter.
Tool name: The tool for translating XML to FPP is called
fpp-from-xml.
Tool behavior:
Unlike the tools described above, fpp-from-xml does not read
from standard input.
To use it, you must name one or more XML files on the command line.
The reason is that the XML parsing library used by the tool requires
named files.
The tool reads the XML files you name, translates them, and
writes the result to standard output.
As an example, try this:
% cat > SSerializable.xml
<serializable name="S">
<members>
<member name="x" type="U32">
</member>
<member name="y" type="F32">
</member>
</members>
</serializable>
^D
% fpp-from-xml SSerializableAi.xml
struct S {
x: U32
y: F32
}
(The formula cat > file lets us enter input to
the console and have it written to file.)
Default values: There are two issues to note in connection with translating default values.
First, in FPP, every definition has a default value, but
the default value need not be given explicitly:
if you provide no explicit default value, then an implicit default is used.
By contrast, in F Prime XML, (1) you must supply default values for array
elements, and (2) you may supply default values for struct members
or enumerations.
To keep the translation simple, if default values are present in the XML
representation, then fpp-from-xml translates them to explicit values,
even if they could be made implicit.
Here is an example:
% cat > AArrayAi.xml
<array name="A">
<type>U32</type>
<size>3</size>
<format>%u</format>
<default>
<value>0</value>
<value>0</value>
<value>0</value>
</default>
</array>
^D
% fpp-from-xml AArrayAi.xml
array A = [3] U32 default [
0
0
0
]
Notice that the implicit default value [ 0, 0, 0 ] becomes
explicit when translating to XML and back to FPP.
Second, to keep the translation simple, only literal numeric values,
literal string values, literal Boolean values, and C++ qualified identifiers
(e.g., a or A::B) are translated.
Other values (e.g., values specified with C++ constructor calls), are not translated.
The reason is that the types of these values cannot be easily inferred from the
XML representation.
When a default value is not translated, the translator inserts an annotation
identifying what was not translated, so that you can do the translation
yourself.
For example, try this:
% cat > AArrayAi.xml
<array name="A">
<include_header>T.hpp</include_header>
<type>T</type>
<size>3</size>
<format>%s</format>
<default>
<value>T()</value>
<value>T()</value>
<value>T()</value>
</default>
</array>
^D
% fpp-from-xml AArrayAi.xml
@ FPP from XML: could not translate array value [ T(), T(), T() ]
array A = [3] T
The tool cannot translate the value T().
So it adds an annotation stating that.
In this case, T() is the default value associated with the
abstract type T, so using the implicit default is correct.
So in this case, just delete the annotation.
Here is another example:
% cat > BArrayAi.xml
<array name="B">
<import_array_type>AArrayAi.xml</import_array_type>
<type>A</type>
<size>2</size>
<format>%s</format>
<default>
<value>A(1, 2)</value>
<value>A(3, 4)</value>
</default>
</array>
^D
% fpp-from-xml BArrayAi.xml
@ FPP from XML: could not translate array value [ A(1, 2), A(3, 4) ]
array B = [2] A
Here the XML representation of the array values [ 1, 2 ] and [ 3, 4 ]
uses the C++ constructor calls A(1, 2) and A(3, 4).
When translating BArrayAi.xml, fpp-from-xml doesn’t know how to translate
those values, because it doesn’t have any information about the type A.
So it omits the FPP default array value and reports the XML default element
values in the annotation.
That way, you can manually construct a default value in FPP.
Inline enum definitions: The following F Prime XML formats may include inline enum definitions:
-
In the Serializable XML format, enumerations may appear as member types.
-
In the Port XML format, enumerations may appear as the types of arguments or as the return type.
-
In the XML formats for commands and for events, enumerations may appear as the types of arguments.
-
In the XML formats for telemetry channels and for parameters, enumerations may appear as the types of data elements.
In each case, the enumerated constants are specified as part of the definition of the member, argument, return type, etc.
FPP does not represent these inline enum definitions directly.
In FPP, enum definitions are always named, so they can be reused.
Therefore, when translating an F Prime XML file that contains inline enum
definitions, fpp-from-xml does the following: (1) translate
each inline definition to a named FPP enum; and (2) use the corresponding named
types in the translated FPP struct or port.
For example, here is an F Prime Serializable XML type
N::S1 containing a member m whose type is an enum
E with three enumerated constants A, B, and C:
cat > S1SerializableAi.xml
<serializable namespace="N" name="S1">
<members>
<member name="m" type="ENUM">
<enum name="E">
<item name="A"/>
<item name="B"/>
<item name="C"/>
</enum>
</member>
</members>
</serializable>
^D
Running fpp-from-xml on this file yields the following:
% fpp-from-xml S1SerializableAi.xml
module N {
enum E {
A = 0
B = 1
C = 2
}
struct S1 {
m: E
}
}
Notice the following:
-
The tool translates namespace
Nin XML to moduleNin FPP. -
The tool translates Serializable type
S1in namespaceNto struct typeS1in moduleN. -
The tool generates an enum type
N.Eto represent the type of membermof structN.S1. -
The tool assigns member
mof structN.S1the typeN.E.
Format strings:
fpp-from-xml translates XML format strings to FPP
format strings, if it can.
Here is an example:
% cat > AArrayAi.xml
<array name="A">
<type>F32</type>
<size>3</size>
<format>%f</format>
<default>
<value>0.0f</value>
<value>0.0f</value>
<value>0.0f</value>
</default>
</array>
^D
Notice that this code contains the line
<format>%f</format>
which is the XML representation of the format.
Now try this:
% fpp-from-xml AArrayAi.xml
array A = [3] F32 default [
0.0
0.0
0.0
] format "{f}"
The XML format %f is translated back to the FPP format {f}.
If the tool cannot translate the format, it will insert an annotation
stating that. For example, %q is not a format recognized by
FPP, so a format containing this string won’t be translated:
% cat > AArrayAi.xml
<array name="A">
<type>F32</type>
<size>1</size>
<format>%q</format>
<default>
<value>0.0</value>
</default>
</array>
^D
% fpp-from-xml AArrayAi.xml
@ FPP from XML: could not translate format string "%q"
array A = [1] F32 default [
0.0
]
Import directives:
XML directives that import symbols (such as import_port_type)
are ignored in the translation.
These directives represent dependencies between XML files, which
become dependencies between FPP source files in the FPP translation.
Once the XML-to-FPP translation is done, you can handle these
dependencies in the ordinary way for FPP, as discussed in the
section on specifying models as files.
XML directives that import XML dictionaries are translated
to
include specifiers.
For example, suppose that CComponentAi.xml defines component C
and contains the directive
<import_dictionary>Commands.xml</import_dictionary>Running fpp-from-xml on CComponentAi.xml produces an
FPP definition of a component C; the component definition
contains the include specifier
include "Commands.fppi"Separately, you can use fpp-from-xml to translate Commands.xml
to Commands.fppi.
17. Writing C Plus Plus Implementations
When constructing an F Prime deployment in C++, there are generally five kinds of implementations you have to write:
-
Implementations of abstract types. These are types that are named in the FPP model but are defined directly in C++.
-
Implementations of external state machines.
-
Implementations of components.
-
Implementations of any libraries used by the component implementations, e.g., algorithm libraries or hardware device driver libraries.
-
A top-level implementation including a
mainfunction for running the FSW application.
Implementing a component (item 3) involves filling out the API provided by the C++ component base class. This process is covered in detail in the F Prime user’s guide; we won’t cover it further here. Similarly, implementing libraries (item 4) is unrelated to FPP, so we won’t cover it in this manual. Here we focus on items 1, 2, and 5: implementing abstract types, implementing external state machines, and implementing deployments. We also discuss serialization of data values, i.e., representing FPP data values as binary data for storage and transmission.
17.1. Implementing Abstract Types
When translating to C++, an
abstract type definition
represents a C++ class that you write directly in C++.
When you use an abstract type T in an FPP definition D (for example, as the
member type of an array definition)
and you translate D to C++, then the generated C++ for D contains an
include directive that includes a header file for T.
As an example, try this:
% fpp-to-cpp -p $PWD type T array A = [3] T ^D
Notice that we used the option -p $PWD.
This is to make the generated include path relative to the current directory.
Now run
% cat AArrayAc.hpp
You should see the following line in the generated C++:
#include "T.hpp"This line says that in order to compile AArrayAc.cpp,
a header file T.hpp must exist in the current directory.
It is up to you to provide that header file.
General implementations:
In most cases, when implementing an abstract type T in C++, you
will define
a class that extends Fw::Serializable from the F Prime framework.
Your class definition should include the following:
-
An implementation of the virtual function
Fw::SerializeStatus T::serializeTo( Fw::SerialBufferBase&, Fw::Endianness = Fw::Endianness::BIG ) const
that specifies how to serialize a class instance to a buffer (i.e., convert a class instance to a byte string stored in a buffer).
-
An implementation of the function
Fw::SerializeStatus T::deserializeFrom( Fw::SerialBufferBase&, Fw::Endianness = Fw::Endianness::BIG )
that specifies how to deserialize a class instance from a buffer (i.e., reconstruct a class instance from a byte string stored in a buffer).
-
A constant
T::SERIALIZED_SIZEthat specifies the size in bytes of a byte string serialized from the class. -
A zero-argument constructor
T(). -
An overloaded equality operator
bool operator==(const T& that) const;
For more on serialization, see the section on serialization of FPP values.
Here is a minimal complete implementation of an abstract type T.
It has one member variable x of type U32 and no methods other than
those required by F Prime.
We have made T a C++ struct (rather than a class) so that
all members are public by default.
To implement serializeTo, we use the serializeFrom function
provided by Fw::SerialBufferBase.
// A minimal implementation of abstract type T
#ifndef T_HPP
#define T_HPP
// Include Fw/Types/Serializable.hpp from the F Prime framework
#include "Fw/Types/Serializable.hpp"
struct T final : public Fw::Serializable { // Extend Fw::Serializable
// Define some shorthand for F Prime types
using SS = Fw::SerializeStatus SS;
using B = Fw::SerialBufferBase B;
using E = Fw::Endianness E;
// Define the constant SERIALIZED_SIZE
enum Constants { SERIALIZED_SIZE = sizeof(U32) };
// Provide a zero-argument constructor
T() : x(0) { }
// Define a comparison operator
bool operator==(const T& that) const { return this->x == that.x; }
// Define the virtual serializeTo method
SS serializeTo(B& b, E e) const final { return b.serializeFrom(x, e); }
// Define the virtual deserializeFrom method
SS deserializeFrom(B& b, E e) final { return b.deserializeTo(x, e); }
// Provide some data
U32 x;
};
#endif
Serializable buffers used in ports:
In some cases, you may want to define an abstract type T that represents
a data buffer and that is used only in port definitions.
In this case you can implement
T as a class that extends Fw::SerialBufferBase.
Instead of implementing the serializeTo and deserializeFrom functions
directly, you override functions that get the address and the capacity
(allocated size) of the buffer; the base class Fw::SerialBufferBase
uses these functions to implement serializeTo and deserializeFrom.
For an example of how to do this, see the files Fw/Cmd/CmdArgBuffer.hpp
and Fw/Cmd/CmdArgBuffer.cpp in the F Prime repository.
Be careful, though: if you implement an abstract type T this way
and you try to use the type T outside of a port definition,
the generated C++ may not compile.
17.2. Implementing External State Machines
An external state machine refers to a state machine implementation supplied outside the FPP model. To implement an external state machine, you can use the State Autocoding for Real-Time Systems (STARS) tool. STARS provides several ways to specify state machines, and it provides several C++ back ends. The F Prime back end is designed to work with FPP code generation.
For an example of an external state machine implemented in STARS,
see FppTest/state_machine in the F Prime repository.
17.3. Implementing Deployments
At the highest level of an F Prime implementation, you write two units of C++ code:
-
Application-specific definitions visible both to the
mainfunction and to the auto-generated topology code. -
The
mainfunction.
We describe each of these code units below.
17.3.1. Application-Specific Definitions
As discussed in the section on
generating C++ topology definitions, when you translate an FPP
topology T to C++, the result goes into files
T TopologyAc.hpp and T TopologyAc.cpp.
The generated file T TopologyAc.hpp includes a file
T TopologyDefs.hpp.
The purpose of this file inclusion is as follows:
-
T
TopologyDefs.hppis not auto-generated. You must write it by hand as part of your C++ implementation. -
Because T
TopologyAc.cppincludes TTopologyAc.hppand TTopologyAc.hppincludes TTopologyDefs.hpp, the handwritten definitions in TTopologyDefs.hppare visible to the auto-generated code in TTopologyAc.hppandTopologyAc.cpp. -
You can also include T
TopologyDefs.hppin your main function (described in the next section) to make its definitions visible there. That waymainand the auto-generated topology code can share these custom definitions.
T TopologyDefs.hpp
must be located in the same directory where the topology T is defined.
When writing the file T TopologyDefs.hpp, you should
follow the description given below.
Topology state:
T TopologyDefs.hpp must define a type
TopologyState in the C++ namespace
corresponding to the FPP module where the topology T is defined.
For example, in SystemReference/Top/topology.fpp in the
F Prime system reference deployment, the FPP topology SystemReference is defined in the FPP
module SystemReference, and so in
SystemReference/Top/SystemReferenceTopologyDefs.hpp, the type TopologyState
is defined in the namespace SystemReference.
TopologyState may be any type.
Usually it is a struct or class.
The C++ code generated by FPP passes a value state of type TopologyState into
each of the functions for setting up and tearing down topologies.
You can read this value in the code associated with your
init specifiers.
In the F Prime system reference example, TopologyState
is a struct with two member variables: a C-style string
hostName that stores a host name and a U32 value portNumber
that stores a port number.
The main function defined in Main.cpp parses the command-line
arguments to the application, uses the result to create an object
state of type TopologyState, and passes the state object
into the functions for setting up and tearing down the topology.
The startTasks phase for the comDriver instance uses the state
object in the following way:
phase Fpp.ToCpp.Phases.startTasks """
// Initialize socket server if and only if there is a valid specification
if (state.hostName != nullptr && state.portNumber != 0) {
Os::TaskString name("ReceiveTask");
// Uplink is configured for receive so a socket task is started
comDriver.configure(state.hostName, state.portNumber);
comDriver.startSocketTask(
name,
true,
ConfigConstants::SystemReference_comDriver::PRIORITY,
ConfigConstants::SystemReference_comDriver::STACK_SIZE
);
}
"""In this code snippet, the expressions state.hostName and state.portNumber
refer to the hostName and portNumber member variables of the
state object passed in from the main function.
The state object is passed in to the setup and teardown functions
via const reference.
Therefore, you may read, but not write, the state object in the
code associated with the init specifiers.
Health ping entries:
If your topology uses an instance of the standard component Svc::Health for
monitoring
the health of components with threads, then T TopologyDefs.hpp
must define the health ping entries used by the health component instance.
The health ping entries specify the time in seconds to wait for the
receipt of a health ping before declaring a timeout.
For each component being monitored, there are two timeout intervals:
a warning interval and a fatal interval.
If the warning interval passes without a health ping, then a warning event occurs.
If the fatal interval passes without a health ping, then a fatal event occurs.
You must specify the health ping entries in the namespace corresponding to the FPP module where T is defined. To specify the health ping entries, you do the following:
-
Open a namespace
PingEntries. -
In that namespace, open a namespace corresponding to the name of each component instance with health ping ports.
-
Inside namespace in item 2, define a C++ enumeration with the following constants
WARNandFATAL. SetWARNequal to the warning interval for the enclosing component instance. SetFATALequal to the fatal interval.
For example, here are the health ping entries from
SystemReference/Top/SystemReferenceTopologyDefs.hpp
in the F Prime system reference repository:
namespace SystemReference {
...
// Health ping entries
namespace PingEntries {
namespace SystemReference_blockDrv { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_chanTlm { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_cmdDisp { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_cmdSeq { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_eventLogger { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_fileDownlink { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_fileManager { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_fileUplink { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_imageProcessor { enum {WARN = 3, FATAL = 5}; }
namespace SystemReference_prmDb { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_processedImageBufferLogger { enum {WARN = 3, FATAL = 5}; }
namespace SystemReference_rateGroup1Comp { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_rateGroup2Comp { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_rateGroup3Comp { enum { WARN = 3, FATAL = 5 }; }
namespace SystemReference_saveImageBufferLogger { enum { WARN = 3, FATAL = 5 }; }
}
}Other definitions:
You can put any compile-time definitions you wish into T TopologyAc.hpp
If you need link-time definitions (e.g., to declare variables with storage),
you can put them in T TopologyAc.cpp, but this is not required.
For example, SystemReference/Top/SystemReferenceTopologyAc.hpp declares
a variable SystemReference::Allocation::mallocator of type Fw::MallocAllocator.
It provides an allocator used in the setup and teardown
of several component instances.
The corresponding link-time symbol is defined in SystemReferenceTopologyDefs.cpp.
17.3.2. The Main Function
You must write a main function that performs application-specific
and system-specific tasks such as parsing command-line arguments,
handling signals, and returning a numeric code to the system on exit.
Your main code can use the following public interface provided
by T TopologyAc.hpp:
// ----------------------------------------------------------------------
// Public interface functions
// ----------------------------------------------------------------------
//! Set up the topology
void setup(
const TopologyState& state //!< The topology state
);
//! Tear down the topology
void teardown(
const TopologyState& state //!< The topology state
);These functions reside in the C++ namespace corresponding to the FPP module where the topology T is defined.
On Linux, a typical main function might work this way:
-
Parse command-line arguments. Use the result to construct a
TopologyStateobjectstate. -
Set up a signal handler to catch signals.
-
Call T
::setup, passing in thestateobject, to construct and initialize the topology. -
Start the topology running, e.g., by looping in the main thread until a signal is handled, or by calling a start function on a timer component (see, e.g.,
Svc::LinuxTimer). The loop or timer typically runs until a signal is caught, e.g., when the user presses control-C at the console. -
On catching a signal
-
Set a flag that causes the main loop to exit or the timer to stop. This flag must be a volatile and atomic variable (e.g.,
std::atomic_bool) because it is accessed concurrently by signal handlers and threads. -
Call T
::teardown, passing in thestateobject, to tear down the topology. -
Wait some time for all the threads to exit.
-
Exit the main thread.
-
For an example like this, see SystemReference/Top/Main.cpp in the
F Prime system reference repository.
17.3.3. Public Symbols
The header file T TopologyAc.hpp declares several public
symbols that you can use when writing your main function.
Instance variables:
Each component instance used in the topology is declared as
an extern variable, so you can refer to any component instance
in the main function.
For example, the main function in the SystemReference topology
calls the method callIsr of the blockDrv (block driver)
component instance, in order to simulate an interrupt service
routine (ISR) call triggered by a hardware interrupt.
Helper functions:
The auto-generated setup function calls the following auto-generated
helper functions:
void initComponents(const TopologyState& state);
void configComponents(const TopologyState& state);
void setBaseIds();
void connectComponents();
void regCommands();
void readParameters();
void loadParameters();
void startTasks(const TopologyState& state);The auto-generated teardown function calls the following
auto-generated helper functions:
void stopTasks(const TopologyState& state);
void freeThreads(const TopologyState& state);
void tearDownComponents(const TopologyState& state);The helper functions are declared as public symbols in T
TopologyAc.hpp, so if you wish, you may write your own versions
of setup and teardown that call these functions directly.
The FPP modeling is designed so that you don’t have to do this;
you can put any custom C++ code for setup or teardown into
init specifiers
and let the FPP translator generate complete setup and teardown
functions that you simply call, as described above.
Using init specifiers generally produces cleaner integration between
the model and the C++ code: you write the custom
C++ code once, any topology T that uses an instance I will pick
up the custom C++ code for I, and the FPP translator will automatically
put the code for I into the correct place in T TopologyAc.cpp.
However, if you wish to write the custom code directly into your main
function, you may.
17.4. Serialization of FPP Values
Every value represented in FPP can be serialized, i.e., converted into a machine-independent sequence of bytes. Serialization provides a consistent way to store data (e.g., to onboard storage) and to transmit data (e.g., to or from the ground). The F Prime framework also uses serialization to pass data through asynchronous port invocations. The data is serialized when it is put on a message queue and then deserialized (i.e., converted from a byte sequence to a C++ representation) when it is taken off the queue for processing.
F Prime uses the following rules for serializing data:
-
Values of primitive integer type are serialized as follows:
-
A value of unsigned integer type (
U8,U16,U32, orU64) is serialized into big-endian order (most significant byte first) by default, using the number of bytes implied by the bit width. For example, theU16value 10 (decimal) is serialized as the two bytes000A(hex). If little-endian order is desired, the optional mode parameter can be specified asFw::Serialization::LITTLE. This stores the data least significant byte order. TheU16value 10 (decimal) is serialized in little-endian as the two bytes0A00(hex). -
A value of signed integer type (
I8,I16,I32, orI64) is serialized by first converting the value to an unsigned value of the same bit width and then serializing the unsigned value as stated in rule 1.a. If the value is nonnegative, then the unsigned value is the same as the signed value. Otherwise the unsigned value is the two’s complement of the signed value. For example:-
The
I16value 10 (decimal) is serialized as two bytes, yielding the bytes000A(hex) in big-endian and0A00(hex) in little-endian. -
The
I16value -10 (decimal) is serialized by (1) computing theU16value 216 - 10 = 65526 and (2) serializing that value as two bytes in the selected byte order, yielding the bytesFFF6(hex) big-endian andF6FF(hex) little-endian.
-
-
-
A value of floating-point type (
F32orF64) is serialized in the selected byte order according to the IEEE standard for representing these values. -
A value of Boolean type is serialized as a single byte. The byte values used to represent
trueandfalseareFW_SERIALIZE_TRUE_VALUEandFW_SERIALIZE_FALSE_VALUE, which are defined in the F Prime configuration headerFpConfig.h. -
A value of string type is serialized as a size followed by the string characters in string order.
-
The size is serialized according to rule 1 for primitive integer types. The F Prime type definition
FwSizeStoreTypespecifies the type to use for the size. This type definition is user-configurable; it is found in the F Prime configuration fileFpConfig.fpp. -
There is one byte for each character of the string, and there is no null terminator. Each string character is serialized as an
I8value according to rule 1.b.
-
-
A value of array type is serialized as a sequence of serialized values, one for each array element, in array order. Each value is serialized using these rules.
-
A value of struct type is serialized member-by-member, in the order that the members appear in the FPP struct definition, with no padding.
-
Except for member arrays, each member is serialized using these rules.
-
Each member array is serialized as stated in rule 5.
-
-
A value of enum type is converted to a primitive integer value of the representation type specified in the enum definition. This value is serialized as stated in rule 1.
-
A value of abstract type is serialized according to its C++ implementation.